Question Number 88430 by ajfour last updated on 10/Apr/20
Commented by ajfour last updated on 10/Apr/20
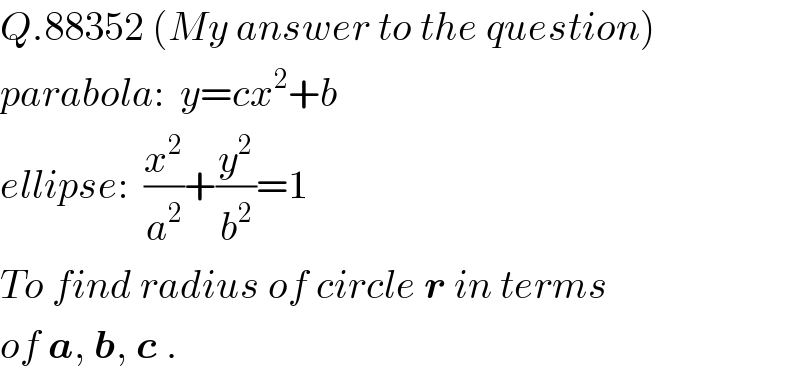
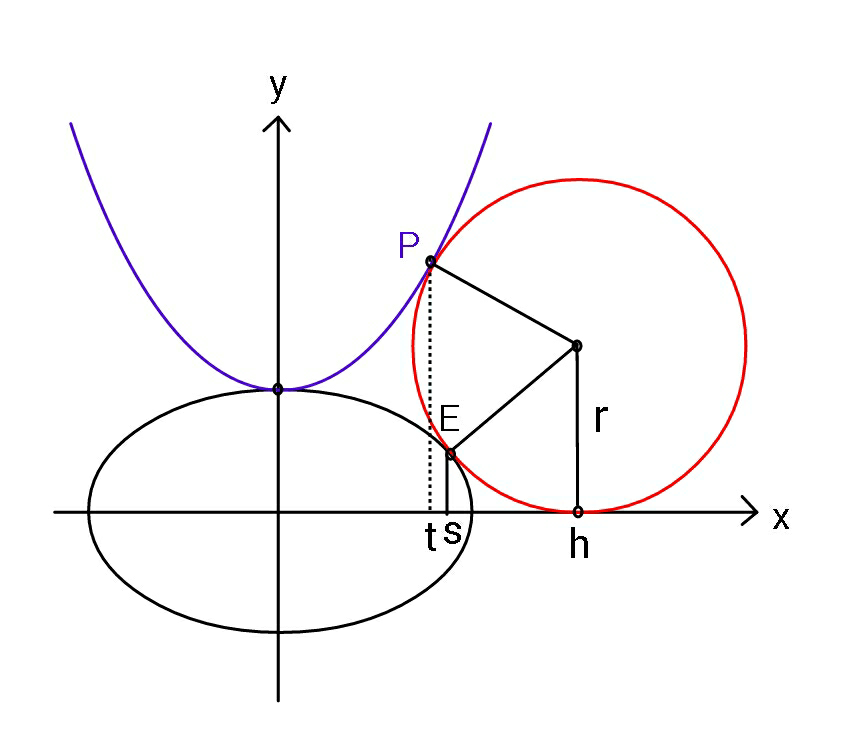
$${Q}.\mathrm{88352}\:\left({My}\:{answer}\:{to}\:{the}\:{question}\right) \\ $$$${parabola}:\:\:{y}={cx}^{\mathrm{2}} +{b} \\ $$$${ellipse}:\:\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${To}\:{find}\:{radius}\:{of}\:{circle}\:\boldsymbol{{r}}\:{in}\:{terms} \\ $$$${of}\:\boldsymbol{{a}},\:\boldsymbol{{b}},\:\boldsymbol{{c}}\:. \\ $$
Answered by ajfour last updated on 10/Apr/20
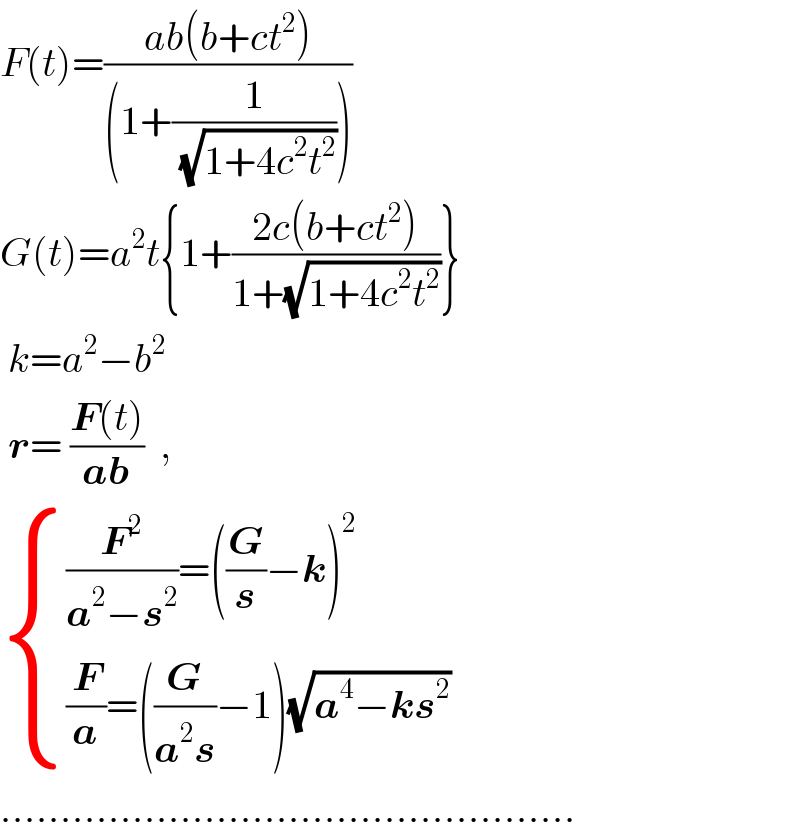
$${F}\left({t}\right)=\frac{{ab}\left({b}+{ct}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{c}^{\mathrm{2}} {t}^{\mathrm{2}} }}\right)} \\ $$$${G}\left({t}\right)={a}^{\mathrm{2}} {t}\left\{\mathrm{1}+\frac{\mathrm{2}{c}\left({b}+{ct}^{\mathrm{2}} \right)}{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{c}^{\mathrm{2}} {t}^{\mathrm{2}} }}\right\} \\ $$$$\:{k}={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$$\:\boldsymbol{{r}}=\:\frac{\boldsymbol{{F}}\left({t}\right)}{\boldsymbol{{ab}}}\:\:,\: \\ $$$$\begin{cases}{\frac{\boldsymbol{{F}}^{\mathrm{2}} }{\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{s}}^{\mathrm{2}} }=\left(\frac{\boldsymbol{{G}}}{\boldsymbol{{s}}}−\boldsymbol{{k}}\right)^{\mathrm{2}} }\\{\frac{\boldsymbol{{F}}}{\boldsymbol{{a}}}=\left(\frac{\boldsymbol{{G}}}{\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{s}}}−\mathrm{1}\right)\sqrt{\boldsymbol{{a}}^{\mathrm{4}} −\boldsymbol{{ks}}^{\mathrm{2}} }}\end{cases} \\ $$$$………………………………………… \\ $$
Commented by mr W last updated on 10/Apr/20

$${the}\:{last}\:{two}\:{equations}\:{represent} \\ $$$${two}\:{curves}: \\ $$$${U}\left({t},{s}\right)=\mathrm{0} \\ $$$${V}\left({t},{s}\right)=\mathrm{0} \\ $$$${we}\:{can}\:{graphically}\:{find}\:{their} \\ $$$${intersection}\:{and}\:{therefore}\:{the} \\ $$$${solution}\:{for}\:{t}\:{as}\:{numerical}\:{value}. \\ $$
