Menu Close

Question-88456

Tinku Tara 0 Comments
Pin




Question Number 88456 by ajfour last updated on 10/Apr/20
Commented by ajfour last updated on 11/Apr/20
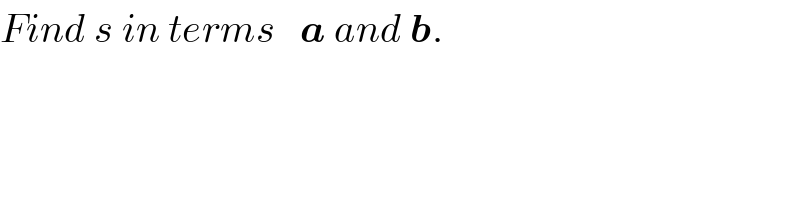
Find s in terms a and b.
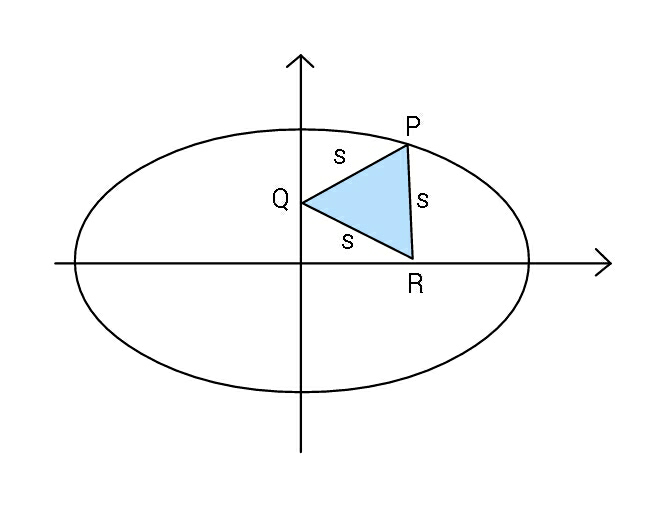
$${Find}\:{s}\:{in}\:{terms}\:\:\:\boldsymbol{{a}}\:{and}\:\boldsymbol{{b}}. \\ $$
Commented by Tony Lin last updated on 11/Apr/20
Commented by Tony Lin last updated on 11/Apr/20
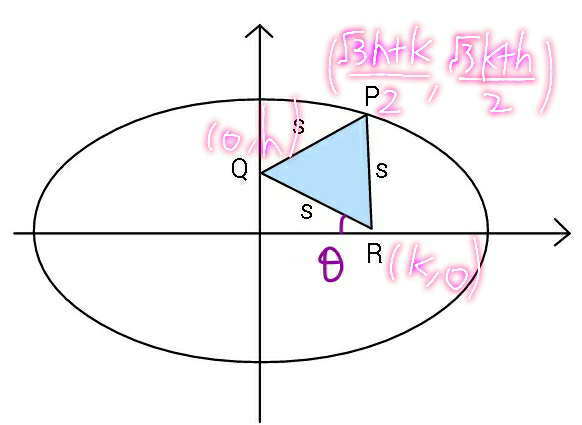
k=scosθ,h=ssinθ [((cos(−60°)),(−sin(−60°))),((sin(−60°)),(cos(−60°))) ] [((−k)),(h) ] = [((((√3)h−k)/2)),((((√3)k+h)/2)) ] P=((((√3)h−k)/2)+k, (((√3)k+h)/2)) =((((√3)h+k)/2), (((√3)k+h)/2)) (x^2 /a^2 )+(y^2 /b^2 )=1 ((((((√3)h+k)/2))^2 )/a^2 )+((((((√3)k+h)/2))^2 )/b^2 )=1 k^2 (b^2 +3a^2 )+h^2 (a^2 +3b^2 )+2(√3)hk(a^2 +b^2 ) s^2 [cos^2 θ(b^2 +3a^2 )+sin^2 θ(a^2 +3b^2 )+(√3)sin2θ(a^2 +b^2 ) =4a^2 b^2 s=(√((4a^2 b^2 )/(cos^2 θ(b^2 +3a^2 )+sin^2 θ(a^2 +3b^2 )+(√3)sin2θ(a^2 +b^2 ))))
$${k}={scos}\theta,{h}={ssin}\theta \\ $$$$\begin{bmatrix}{{cos}\left(−\mathrm{60}°\right)}&{−{sin}\left(−\mathrm{60}°\right)}\\{{sin}\left(−\mathrm{60}°\right)}&{{cos}\left(−\mathrm{60}°\right)}\end{bmatrix}\begin{bmatrix}{−{k}}\\{{h}}\end{bmatrix} \\ $$$$=\begin{bmatrix}{\frac{\sqrt{\mathrm{3}}{h}−{k}}{\mathrm{2}}}\\{\frac{\sqrt{\mathrm{3}}{k}+{h}}{\mathrm{2}}}\end{bmatrix} \\ $$$${P}=\left(\frac{\sqrt{\mathrm{3}}{h}−{k}}{\mathrm{2}}+{k},\:\frac{\sqrt{\mathrm{3}}{k}+{h}}{\mathrm{2}}\right) \\ $$$$=\left(\frac{\sqrt{\mathrm{3}}{h}+{k}}{\mathrm{2}},\:\frac{\sqrt{\mathrm{3}}{k}+{h}}{\mathrm{2}}\right) \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{\left(\frac{\sqrt{\mathrm{3}}{h}+{k}}{\mathrm{2}}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left(\frac{\sqrt{\mathrm{3}}{k}+{h}}{\mathrm{2}}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${k}^{\mathrm{2}} \left({b}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} \right)+{h}^{\mathrm{2}} \left({a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} \right)+\mathrm{2}\sqrt{\mathrm{3}}{hk}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$$${s}^{\mathrm{2}} \left[{cos}^{\mathrm{2}} \theta\left({b}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} \right)+{sin}^{\mathrm{2}} \theta\left({a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} \right)+\sqrt{\mathrm{3}}{sin}\mathrm{2}\theta\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\right. \\ $$$$=\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$${s}=\sqrt{\frac{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{cos}^{\mathrm{2}} \theta\left({b}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} \right)+{sin}^{\mathrm{2}} \theta\left({a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} \right)+\sqrt{\mathrm{3}}{sin}\mathrm{2}\theta\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}} \\ $$
Commented by ajfour last updated on 11/Apr/20
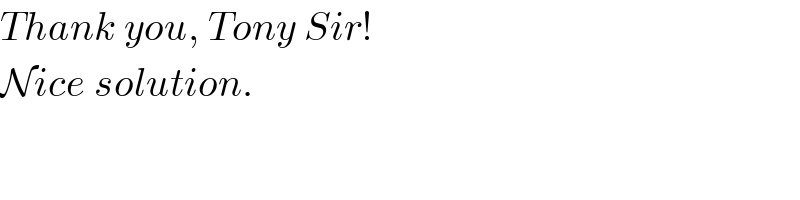
Thank you, Tony Sir! Nice solution.
$${Thank}\:{you},\:{Tony}\:{Sir}! \\ $$$$\mathcal{N}{ice}\:{solution}. \\ $$
Answered by mr W last updated on 11/Apr/20
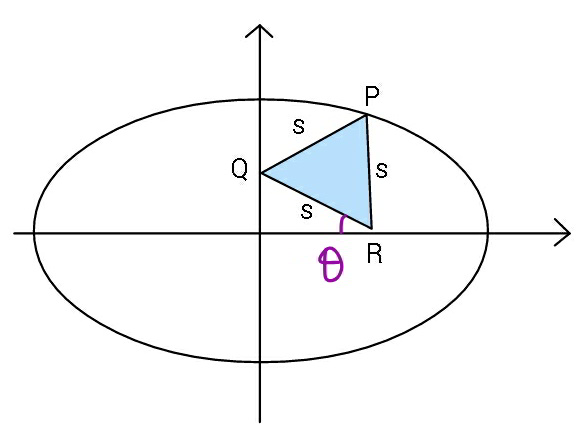
Commented by mr W last updated on 11/Apr/20
y_Q =s sin θ x_P =s cos ((π/3)−θ)=(s/2)(cos θ+(√3) sin θ) y_P =s[sin θ+sin ((π/3)−θ)]=(s/2)(sin θ+(√3) cos θ) b^2 x_P ^2 +a^2 y_P ^2 =a^2 b^2 (s^2 /4)[b^2 (cos θ+(√3) sin θ)^2 +a^2 (sin θ+(√3) cos θ)^2 ]=a^2 b^2 s^2 [b^2 (cos^2 θ+2(√3) sin θ cos θ+3 cos^2 θ)+a^2 (sin^2 θ+2(√3) sin θcos θ+3 sin^2 θ)]=4a^2 b^2 s^2 [(√3)(a^2 + b^2 ) sin 2θ+(a^2 +3b^2 ) sin^2 θ+(3a^2 +b^2 ) cos^2 θ)]=4a^2 b^2 with μ=(b/a) P=((4b^2 )/s^2 )=(√3)(1+ μ^2 ) sin 2θ+(1+3μ^2 ) sin^2 θ+(3+μ^2 ) cos^2 θ P=((4b^2 )/s^2 )=2(1+μ^2 )+(√3)(1+ μ^2 ) sin 2θ+(1−μ^2 )cos 2θ (dP/dθ)=2(√3)(1+ μ^2 ) cos 2θ−2(1−μ^2 ) sin 2θ=0 ⇒tan 2θ=(((1+μ^2 )(√3))/(1−μ^2 )) ⇒sin 2θ=(((1+μ^2 )(√3))/(2(√(1+μ^2 +μ^4 )))) ⇒cos 2θ=((1−μ^2 )/(2(√(1+μ^2 +μ^4 )))) ((4b^2 )/s_(min) ^2 )=2(1+μ^2 )+(√3)(1+ μ^2 )(((1+μ^2 )(√3))/(2(√(1+μ^2 +μ^4 ))))+(1−μ^2 )((1−μ^2 )/(2(√(1+μ^2 +μ^4 )))) ((2b^2 )/s_(min) ^2 )=1+μ^2 +(√(1+μ^2 +μ^4 )) ⇒s_(min) =(((√2)b)/( (√(1+μ^2 +(√(1+μ^2 +μ^4 )))))) example: a=4, b=3, μ=(3/4) ⇒s_(min) =((√(50−2(√(481))))/3)×b=(√(50−2(√(481))))=2.477
$${y}_{{Q}} ={s}\:\mathrm{sin}\:\theta \\ $$$${x}_{{P}} ={s}\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{3}}−\theta\right)=\frac{{s}}{\mathrm{2}}\left(\mathrm{cos}\:\theta+\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\right) \\ $$$${y}_{{P}} ={s}\left[\mathrm{sin}\:\theta+\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\theta\right)\right]=\frac{{s}}{\mathrm{2}}\left(\mathrm{sin}\:\theta+\sqrt{\mathrm{3}}\:\mathrm{cos}\:\theta\right) \\ $$$${b}^{\mathrm{2}} {x}_{{P}} ^{\mathrm{2}} +{a}^{\mathrm{2}} {y}_{{P}} ^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\frac{{s}^{\mathrm{2}} }{\mathrm{4}}\left[{b}^{\mathrm{2}} \left(\mathrm{cos}\:\theta+\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \left(\mathrm{sin}\:\theta+\sqrt{\mathrm{3}}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} \right]={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} \left[{b}^{\mathrm{2}} \left(\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta+\mathrm{3}\:\mathrm{cos}^{\mathrm{2}} \:\theta\right)+{a}^{\mathrm{2}} \left(\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\mathrm{cos}\:\theta+\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)\right]=\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\left.{s}^{\mathrm{2}} \left[\sqrt{\mathrm{3}}\left({a}^{\mathrm{2}} +\:{b}^{\mathrm{2}} \right)\:\mathrm{sin}\:\mathrm{2}\theta+\left({a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} \right)\:\mathrm{sin}^{\mathrm{2}} \:\theta+\left(\mathrm{3}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\:\mathrm{cos}^{\mathrm{2}} \:\theta\right)\right]=\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$${with}\:\mu=\frac{{b}}{{a}} \\ $$$${P}=\frac{\mathrm{4}{b}^{\mathrm{2}} }{{s}^{\mathrm{2}} }=\sqrt{\mathrm{3}}\left(\mathrm{1}+\:\mu^{\mathrm{2}} \right)\:\mathrm{sin}\:\mathrm{2}\theta+\left(\mathrm{1}+\mathrm{3}\mu^{\mathrm{2}} \right)\:\mathrm{sin}^{\mathrm{2}} \:\theta+\left(\mathrm{3}+\mu^{\mathrm{2}} \right)\:\mathrm{cos}^{\mathrm{2}} \:\theta \\ $$$${P}=\frac{\mathrm{4}{b}^{\mathrm{2}} }{{s}^{\mathrm{2}} }=\mathrm{2}\left(\mathrm{1}+\mu^{\mathrm{2}} \right)+\sqrt{\mathrm{3}}\left(\mathrm{1}+\:\mu^{\mathrm{2}} \right)\:\mathrm{sin}\:\mathrm{2}\theta+\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{cos}\:\mathrm{2}\theta \\ $$$$\frac{{dP}}{{d}\theta}=\mathrm{2}\sqrt{\mathrm{3}}\left(\mathrm{1}+\:\mu^{\mathrm{2}} \right)\:\mathrm{cos}\:\mathrm{2}\theta−\mathrm{2}\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\:\mathrm{sin}\:\mathrm{2}\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{2}\theta=\frac{\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\sqrt{\mathrm{3}}}{\mathrm{1}−\mu^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{2}\theta=\frac{\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} +\mu^{\mathrm{4}} }} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{2}\theta=\frac{\mathrm{1}−\mu^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} +\mu^{\mathrm{4}} }} \\ $$$$\frac{\mathrm{4}{b}^{\mathrm{2}} }{{s}_{{min}} ^{\mathrm{2}} }=\mathrm{2}\left(\mathrm{1}+\mu^{\mathrm{2}} \right)+\sqrt{\mathrm{3}}\left(\mathrm{1}+\:\mu^{\mathrm{2}} \right)\frac{\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} +\mu^{\mathrm{4}} }}+\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\frac{\mathrm{1}−\mu^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} +\mu^{\mathrm{4}} }} \\ $$$$\frac{\mathrm{2}{b}^{\mathrm{2}} }{{s}_{{min}} ^{\mathrm{2}} }=\mathrm{1}+\mu^{\mathrm{2}} +\sqrt{\mathrm{1}+\mu^{\mathrm{2}} +\mu^{\mathrm{4}} } \\ $$$$\Rightarrow{s}_{{min}} =\frac{\sqrt{\mathrm{2}}{b}}{\:\sqrt{\mathrm{1}+\mu^{\mathrm{2}} +\sqrt{\mathrm{1}+\mu^{\mathrm{2}} +\mu^{\mathrm{4}} }}} \\ $$$$ \\ $$$${example}:\:{a}=\mathrm{4},\:{b}=\mathrm{3},\:\mu=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow{s}_{{min}} =\frac{\sqrt{\mathrm{50}−\mathrm{2}\sqrt{\mathrm{481}}}}{\mathrm{3}}×{b}=\sqrt{\mathrm{50}−\mathrm{2}\sqrt{\mathrm{481}}}=\mathrm{2}.\mathrm{477} \\ $$
Commented by ajfour last updated on 11/Apr/20
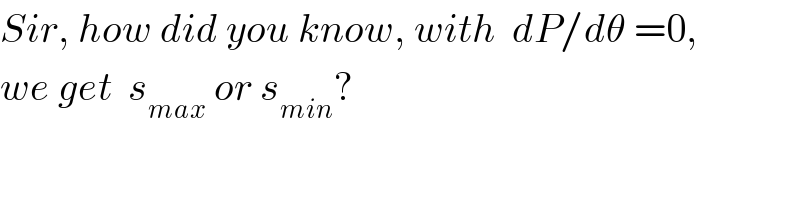
Sir, how did you know, with dP/dθ =0, we get s_(max) or s_(min) ?
$${Sir},\:{how}\:{did}\:{you}\:{know},\:{with}\:\:{dP}/{d}\theta\:=\mathrm{0}, \\ $$$${we}\:{get}\:\:{s}_{{max}} \:{or}\:{s}_{{min}} ? \\ $$
Commented by mr W last updated on 11/Apr/20
Commented by mr W last updated on 11/Apr/20
there are infinite equilateral triangles, (dP/dθ)=0 for max. P which leads to s_(min.)
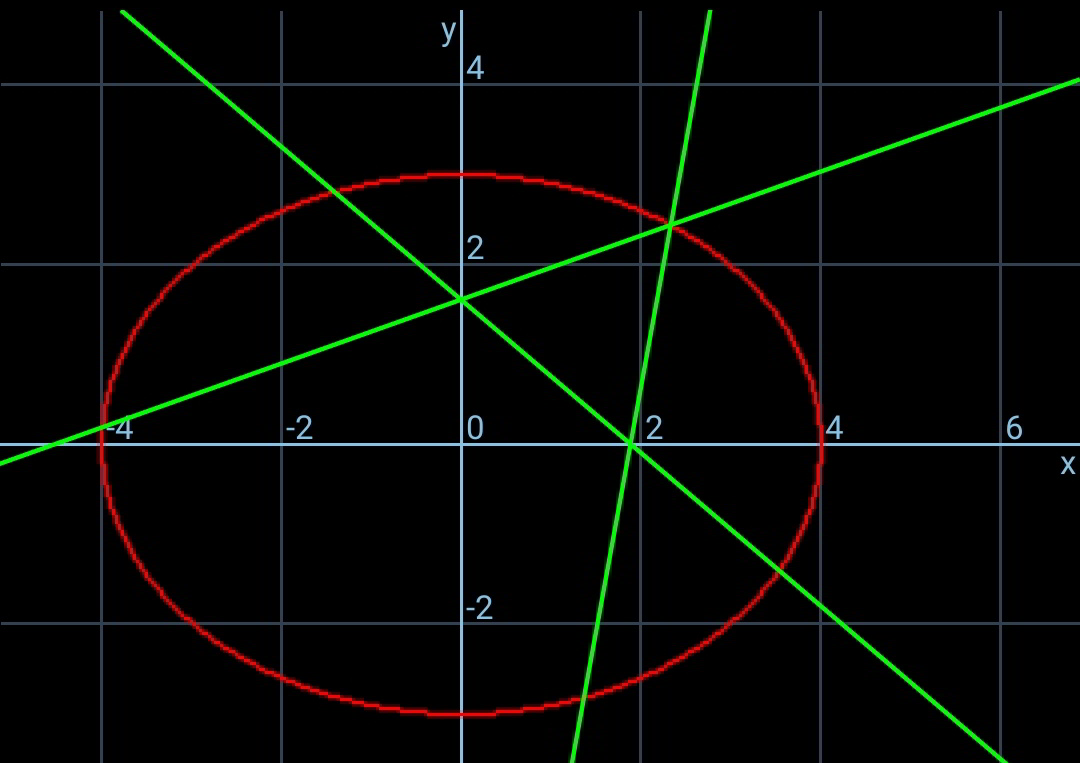
$${there}\:{are}\:{infinite}\:{equilateral}\:{triangles}, \\ $$$$\frac{{dP}}{{d}\theta}=\mathrm{0}\:{for}\:{max}.\:{P}\:{which}\:{leads}\:{to}\:{s}_{{min}.} \\ $$
Commented by ajfour last updated on 11/Apr/20
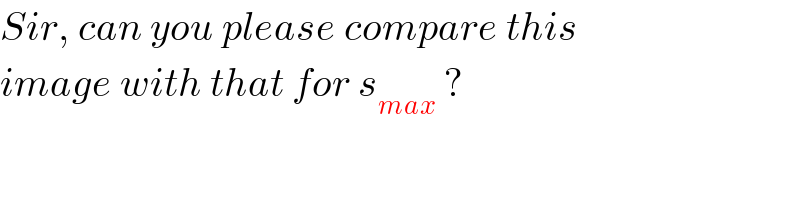
Sir, can you please compare this image with that for s_(max) ?
$${Sir},\:{can}\:{you}\:{please}\:{compare}\:{this} \\ $$$${image}\:{with}\:{that}\:{for}\:{s}_{{max}} \:? \\ $$
Commented by mr W last updated on 11/Apr/20
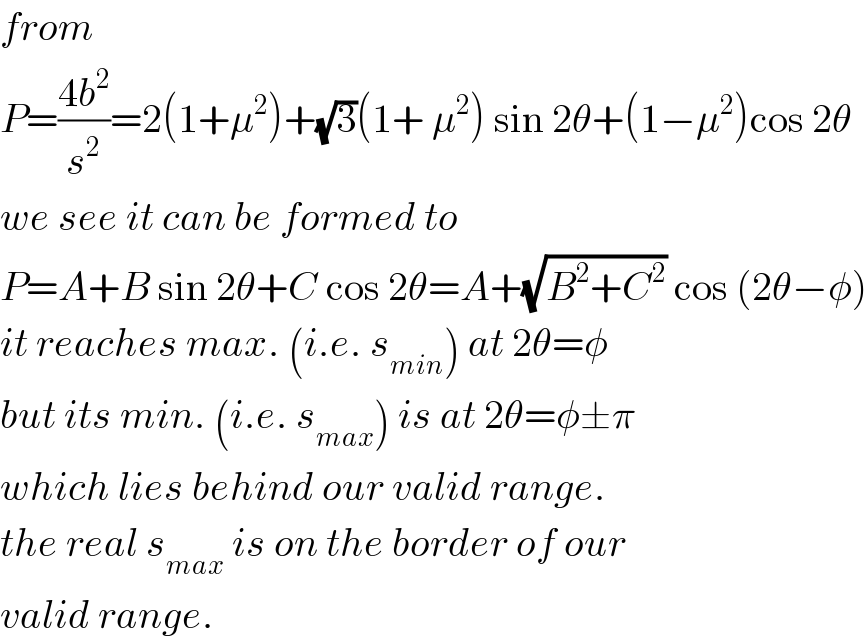
from P=((4b^2 )/s^2 )=2(1+μ^2 )+(√3)(1+ μ^2 ) sin 2θ+(1−μ^2 )cos 2θ we see it can be formed to P=A+B sin 2θ+C cos 2θ=A+(√(B^2 +C^2 )) cos (2θ−φ) it reaches max. (i.e. s_(min) ) at 2θ=φ but its min. (i.e. s_(max) ) is at 2θ=φ±π which lies behind our valid range. the real s_(max) is on the border of our valid range.
$${from} \\ $$$${P}=\frac{\mathrm{4}{b}^{\mathrm{2}} }{{s}^{\mathrm{2}} }=\mathrm{2}\left(\mathrm{1}+\mu^{\mathrm{2}} \right)+\sqrt{\mathrm{3}}\left(\mathrm{1}+\:\mu^{\mathrm{2}} \right)\:\mathrm{sin}\:\mathrm{2}\theta+\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{cos}\:\mathrm{2}\theta \\ $$$${we}\:{see}\:{it}\:{can}\:{be}\:{formed}\:{to} \\ $$$${P}={A}+{B}\:\mathrm{sin}\:\mathrm{2}\theta+{C}\:\mathrm{cos}\:\mathrm{2}\theta={A}+\sqrt{{B}^{\mathrm{2}} +{C}^{\mathrm{2}} }\:\mathrm{cos}\:\left(\mathrm{2}\theta−\phi\right) \\ $$$${it}\:{reaches}\:{max}.\:\left({i}.{e}.\:{s}_{{min}} \right)\:{at}\:\mathrm{2}\theta=\phi \\ $$$${but}\:{its}\:{min}.\:\left({i}.{e}.\:{s}_{{max}} \right)\:{is}\:{at}\:\mathrm{2}\theta=\phi\pm\pi \\ $$$${which}\:{lies}\:{behind}\:{our}\:{valid}\:{range}. \\ $$$${the}\:{real}\:{s}_{{max}} \:{is}\:{on}\:{the}\:{border}\:{of}\:{our} \\ $$$${valid}\:{range}. \\ $$
Commented by mr W last updated on 11/Apr/20
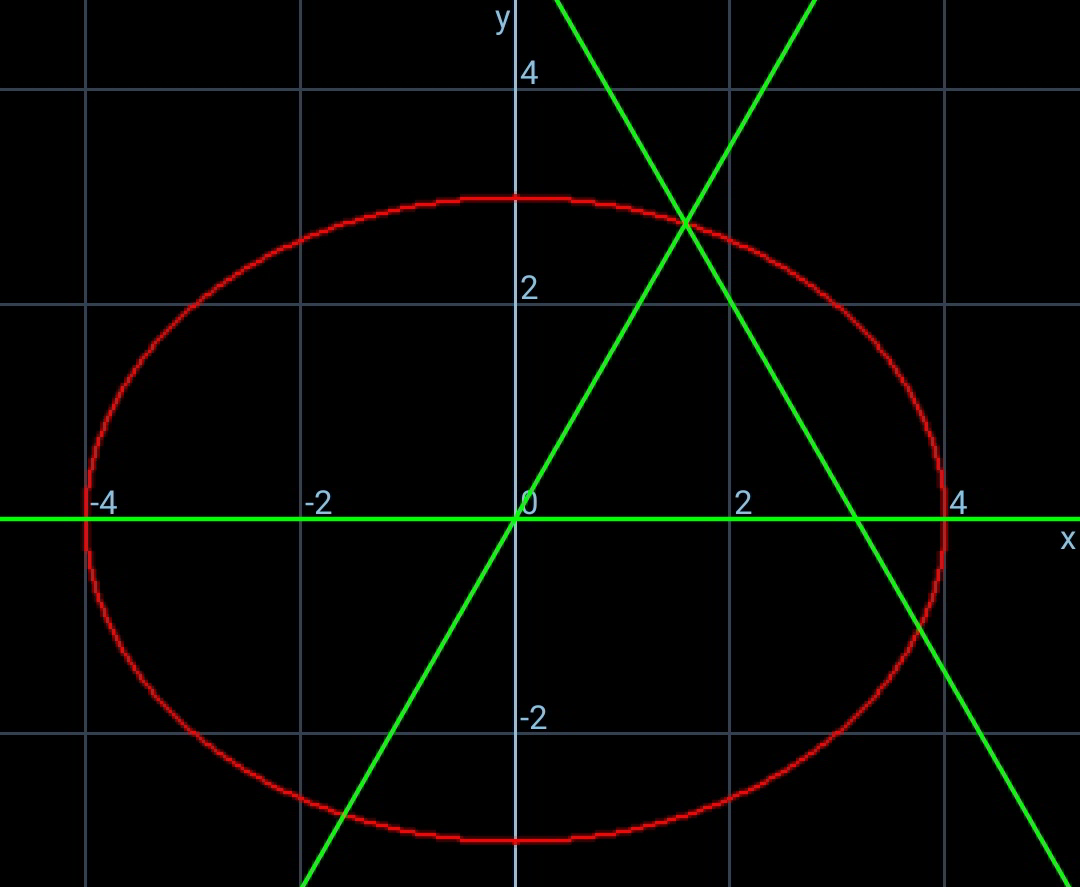
Commented by mr W last updated on 11/Apr/20
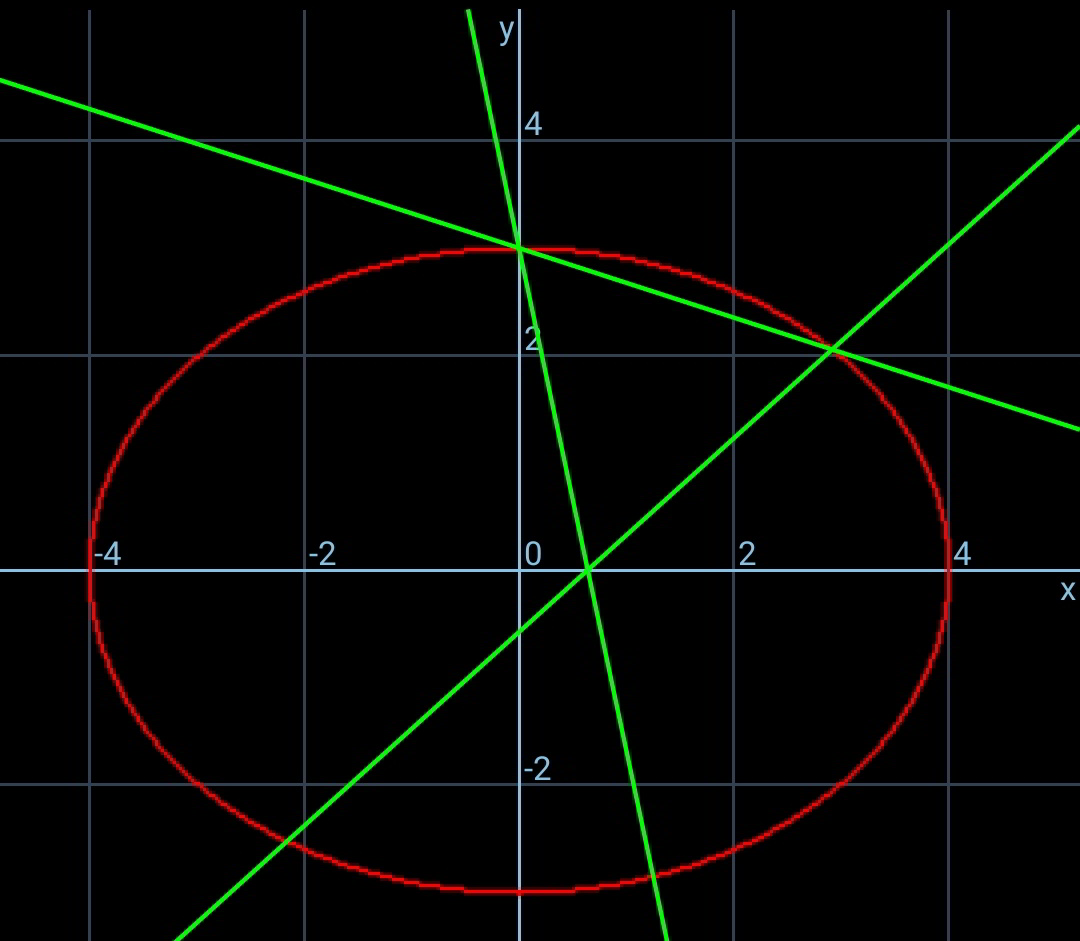
Commented by mr W last updated on 11/Apr/20
since point Q is restricted from (0,0) to (0,b) we can′t get the mathematical maximum s_(max) . the actual s_(max) is one of the two cases above: Q at (0,0) or Q at (0,b). but s_(min) is between both cases, corresponds to (dP/dθ)=0.
$${since}\:{point}\:{Q}\:{is}\:{restricted}\:{from}\:\left(\mathrm{0},\mathrm{0}\right) \\ $$$${to}\:\left(\mathrm{0},{b}\right)\:{we}\:{can}'{t}\:{get}\:{the}\:{mathematical} \\ $$$${maximum}\:{s}_{{max}} .\:{the}\:{actual}\:{s}_{{max}} \:{is} \\ $$$${one}\:{of}\:{the}\:{two}\:{cases}\:{above}:\:{Q}\:{at}\:\left(\mathrm{0},\mathrm{0}\right) \\ $$$${or}\:{Q}\:{at}\:\left(\mathrm{0},{b}\right). \\ $$$${but}\:{s}_{{min}} \:{is}\:{between}\:{both}\:{cases},\: \\ $$$${corresponds}\:{to}\:\frac{{dP}}{{d}\theta}=\mathrm{0}. \\ $$
Commented by ajfour last updated on 11/Apr/20
Thank you Sir! For a=4, b=3_(−) this means for θ=0 we have s_(max) & at some intermediate θ=α, as shown in main solution we have s_(min) , and θ_(max) = β (say) α< β <(π/2) . Complete Treatment Sir! thanks a lot again.
$${Thank}\:{you}\:{Sir}!\:\: \\ $$$$\underset{−} {{For}\:{a}=\mathrm{4},\:{b}=\mathrm{3}} \\ $$$${this}\:{means}\:{for}\:\theta=\mathrm{0}\:{we}\:{have} \\ $$$${s}_{{max}} \:\&\:{at}\:{some}\:{intermediate}\:\theta=\alpha, \\ $$$${as}\:{shown}\:{in}\:{main}\:{solution}\:{we} \\ $$$${have}\:{s}_{{min}} \:,\:{and}\:\theta_{{max}} \:=\:\beta\:\left({say}\right) \\ $$$$\alpha<\:\beta\:<\frac{\pi}{\mathrm{2}}\:. \\ $$$$\mathcal{C}{omplete}\:\mathcal{T}{reatment}\:{Sir}! \\ $$$${thanks}\:{a}\:{lot}\:{again}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *