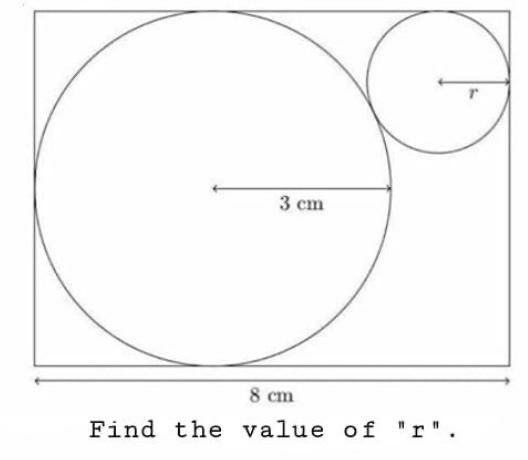
Question Number 88487 by I want to learn more last updated on 11/Apr/20
Commented by I want to learn more last updated on 11/Apr/20

$$\mathrm{Please}\:\mathrm{help}. \\ $$
Commented by jagoll last updated on 11/Apr/20
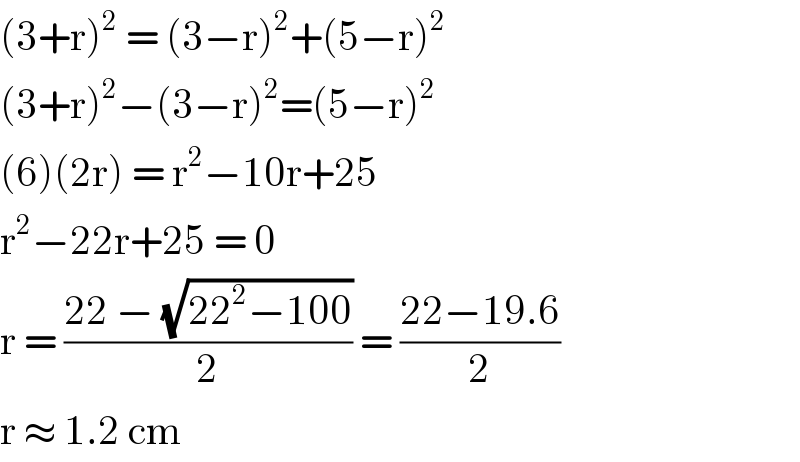
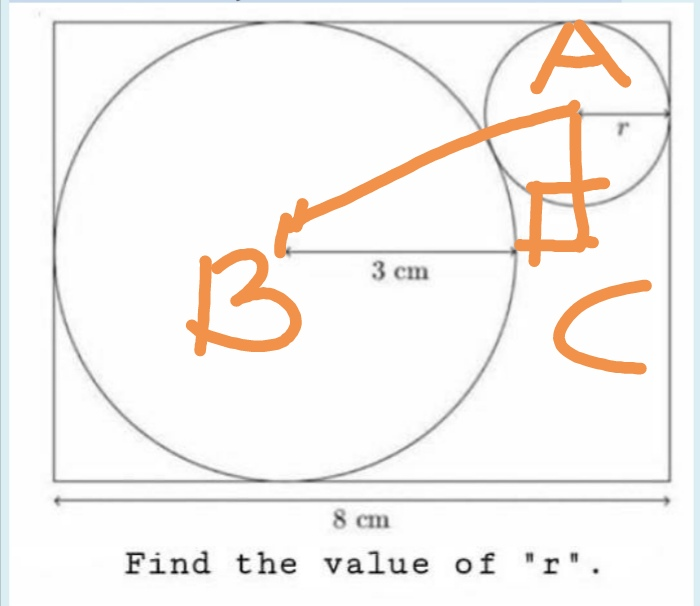
$$\left(\mathrm{3}+\mathrm{r}\right)^{\mathrm{2}} \:=\:\left(\mathrm{3}−\mathrm{r}\right)^{\mathrm{2}} +\left(\mathrm{5}−\mathrm{r}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{3}+\mathrm{r}\right)^{\mathrm{2}} −\left(\mathrm{3}−\mathrm{r}\right)^{\mathrm{2}} =\left(\mathrm{5}−\mathrm{r}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{6}\right)\left(\mathrm{2r}\right)\:=\:\mathrm{r}^{\mathrm{2}} −\mathrm{10r}+\mathrm{25} \\ $$$$\mathrm{r}^{\mathrm{2}} −\mathrm{22r}+\mathrm{25}\:=\:\mathrm{0} \\ $$$$\mathrm{r}\:=\:\frac{\mathrm{22}\:−\:\sqrt{\mathrm{22}^{\mathrm{2}} −\mathrm{100}}}{\mathrm{2}}\:=\:\frac{\mathrm{22}−\mathrm{19}.\mathrm{6}}{\mathrm{2}} \\ $$$$\mathrm{r}\:\approx\:\mathrm{1}.\mathrm{2}\:\mathrm{cm} \\ $$
Commented by $@ty@m123 last updated on 11/Apr/20

$${Nice}…. \\ $$
Commented by I want to learn more last updated on 11/Apr/20
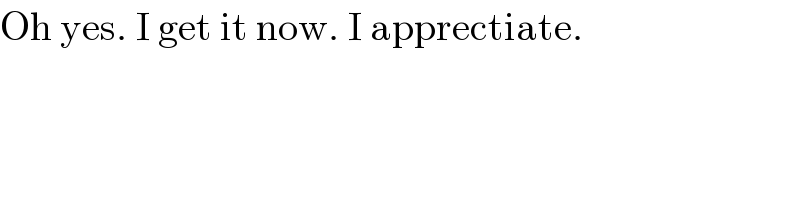
$$\mathrm{Oh}\:\mathrm{yes}.\:\mathrm{I}\:\mathrm{get}\:\mathrm{it}\:\mathrm{now}.\:\mathrm{I}\:\mathrm{apprectiate}. \\ $$
Commented by I want to learn more last updated on 11/Apr/20
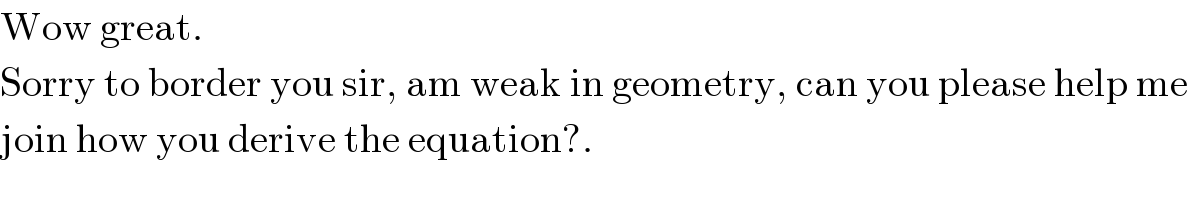
$$\mathrm{Wow}\:\mathrm{great}. \\ $$$$\mathrm{Sorry}\:\mathrm{to}\:\mathrm{border}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{am}\:\mathrm{weak}\:\mathrm{in}\:\mathrm{geometry},\:\mathrm{can}\:\mathrm{you}\:\mathrm{please}\:\mathrm{help}\:\mathrm{me} \\ $$$$\mathrm{join}\:\mathrm{how}\:\mathrm{you}\:\mathrm{derive}\:\mathrm{the}\:\mathrm{equation}?.\: \\ $$
Commented by $@ty@m123 last updated on 11/Apr/20
Commented by $@ty@m123 last updated on 11/Apr/20
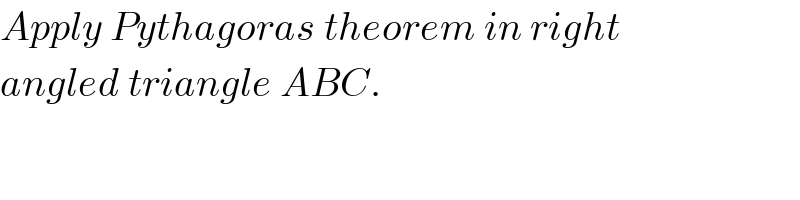
$${Apply}\:{Pythagoras}\:{theorem}\:{in}\:{right} \\ $$$${angled}\:{triangle}\:{ABC}. \\ $$
