Question Number 88656 by ajfour last updated on 12/Apr/20
Commented by ajfour last updated on 12/Apr/20
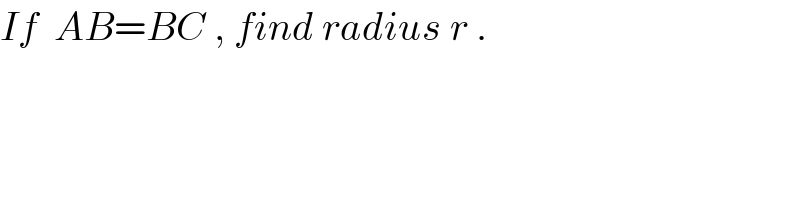
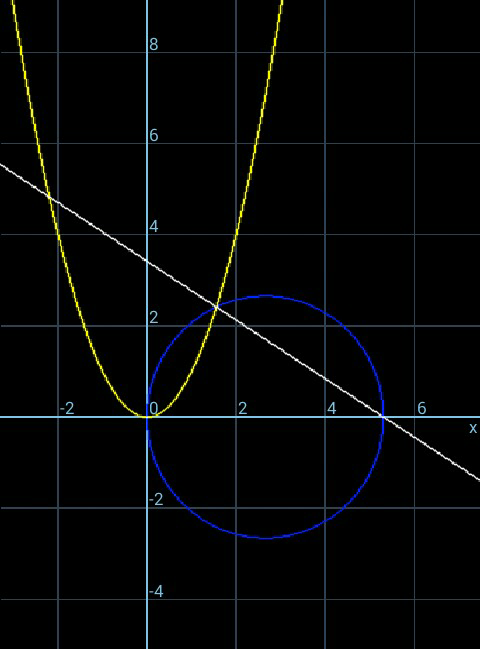
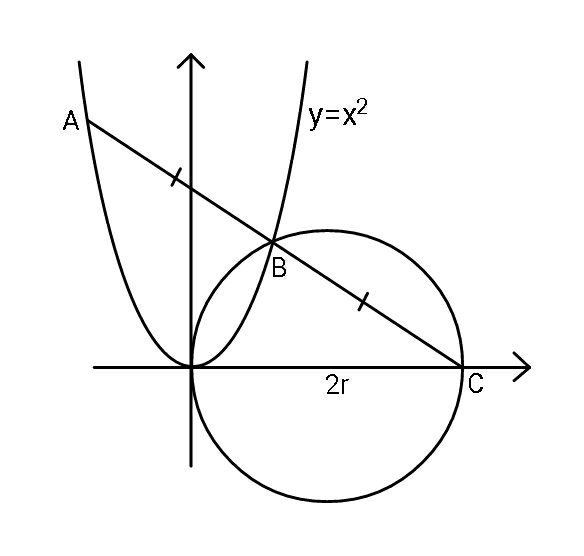
$${If}\:\:{AB}={BC}\:,\:{find}\:{radius}\:{r}\:. \\ $$
Answered by ajfour last updated on 12/Apr/20
![(x−r)^2 +y^2 =r^2 circle y=x^2 parabola (x−r)^2 +x^4 =r^2 ⇒ x^3 +x−2r=0 (besides x=0) say real root is x=a. ⇒ a^3 +a−2r=0 .....(i) eq. of line: y=−((a^2 (x−2r))/((2r−a))) 2r+x_A =2a y_A =x_A ^2 = 4(r−a)^2 y_B = (y_A /2)=2(r−a)^2 =a^2 ⇒ a^2 −4ar+2r^2 =0 ....(ii) & a^3 +a−2r=0 ....(i) (i)−[a×(ii)] gives a+4a^2 r−2r−2ar^2 =0 ⇒ a^2 −((r/2)−(1/(4r)))a−(1/2)=0 a=((r/4)−(1/(8r)))+(√(((r/4)−(1/(8r)))^2 +(1/2))) from (ii): (2r−a)^2 =2r^2 ⇒ {((7r)/4)+(1/(8r))−(√(((r/4)−(1/(8r)))^2 +(1/2))) }^2 = 2r^2 ⇒ r≈ 2.65246](https://www.tinkutara.com/question/Q88659.png)
$$\left({x}−{r}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \:\:\:{circle} \\ $$$${y}={x}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:{parabola} \\ $$$$\left({x}−{r}\right)^{\mathrm{2}} +{x}^{\mathrm{4}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{3}} +{x}−\mathrm{2}{r}=\mathrm{0}\:\:\:\left({besides}\:{x}=\mathrm{0}\right) \\ $$$${say}\:{real}\:{root}\:{is}\:{x}={a}. \\ $$$$\Rightarrow\:\:{a}^{\mathrm{3}} +{a}−\mathrm{2}{r}=\mathrm{0}\:\:\:\:…..\left({i}\right) \\ $$$${eq}.\:{of}\:{line}:\:\:\:{y}=−\frac{{a}^{\mathrm{2}} \left({x}−\mathrm{2}{r}\right)}{\left(\mathrm{2}{r}−{a}\right)} \\ $$$$\mathrm{2}{r}+{x}_{{A}} =\mathrm{2}{a} \\ $$$${y}_{{A}} ={x}_{{A}} ^{\mathrm{2}} \:=\:\mathrm{4}\left({r}−{a}\right)^{\mathrm{2}} \\ $$$${y}_{{B}} =\:\frac{{y}_{{A}} }{\mathrm{2}}=\mathrm{2}\left({r}−{a}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:{a}^{\mathrm{2}} −\mathrm{4}{ar}+\mathrm{2}{r}^{\mathrm{2}} =\mathrm{0}\:\:\:….\left({ii}\right) \\ $$$$\&\:\:\:\:{a}^{\mathrm{3}} +{a}−\mathrm{2}{r}=\mathrm{0}\:\:\:\:\:\:\:\:\:….\left({i}\right) \\ $$$$\left({i}\right)−\left[{a}×\left({ii}\right)\right]\:\:\:{gives} \\ $$$$\:\:{a}+\mathrm{4}{a}^{\mathrm{2}} {r}−\mathrm{2}{r}−\mathrm{2}{ar}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\:{a}^{\mathrm{2}} −\left(\frac{{r}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}{r}}\right){a}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$${a}=\left(\frac{{r}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{8}{r}}\right)+\sqrt{\left(\frac{{r}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{8}{r}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${from}\:\left({ii}\right):\:\:\:\:\left(\mathrm{2}{r}−{a}\right)^{\mathrm{2}} =\mathrm{2}{r}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\left\{\frac{\mathrm{7}{r}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}{r}}−\sqrt{\left(\frac{{r}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{8}{r}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}}\:\right\}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}{r}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{r}\approx\:\mathrm{2}.\mathrm{65246}\: \\ $$
Commented by ajfour last updated on 12/Apr/20