Question Number 88673 by ajfour last updated on 12/Apr/20
Commented by john santu last updated on 12/Apr/20

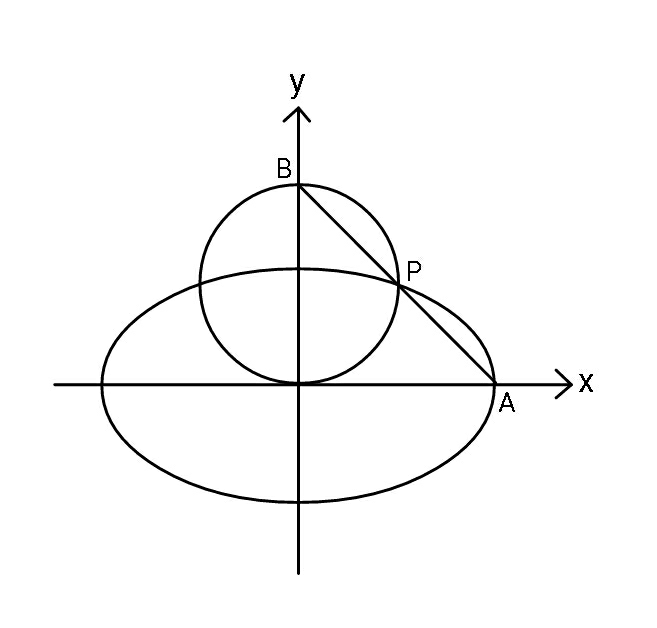
$${eqn}:\:{ellips}\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\:+\:\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$${eqn}:\:{circle}\:{x}^{\mathrm{2}} \:+\left({y}−{r}\right)^{\mathrm{2}} \:=\:{r}^{\mathrm{2}} \\ $$$${eqn}\:{line}\:{AB}\:\Rightarrow\:\mathrm{2}{rx}\:+\:{ay}\:=\:\mathrm{2}{ar} \\ $$
Commented by ajfour last updated on 12/Apr/20

$${Determine}\:{the}\:{radius}\:{of}\:{circle}, \\ $$$${in}\:{terms}\:{of}\:{ellipse}\:{parameters} \\ $$$${a}\:{and}\:{b}. \\ $$
Answered by mr W last updated on 12/Apr/20

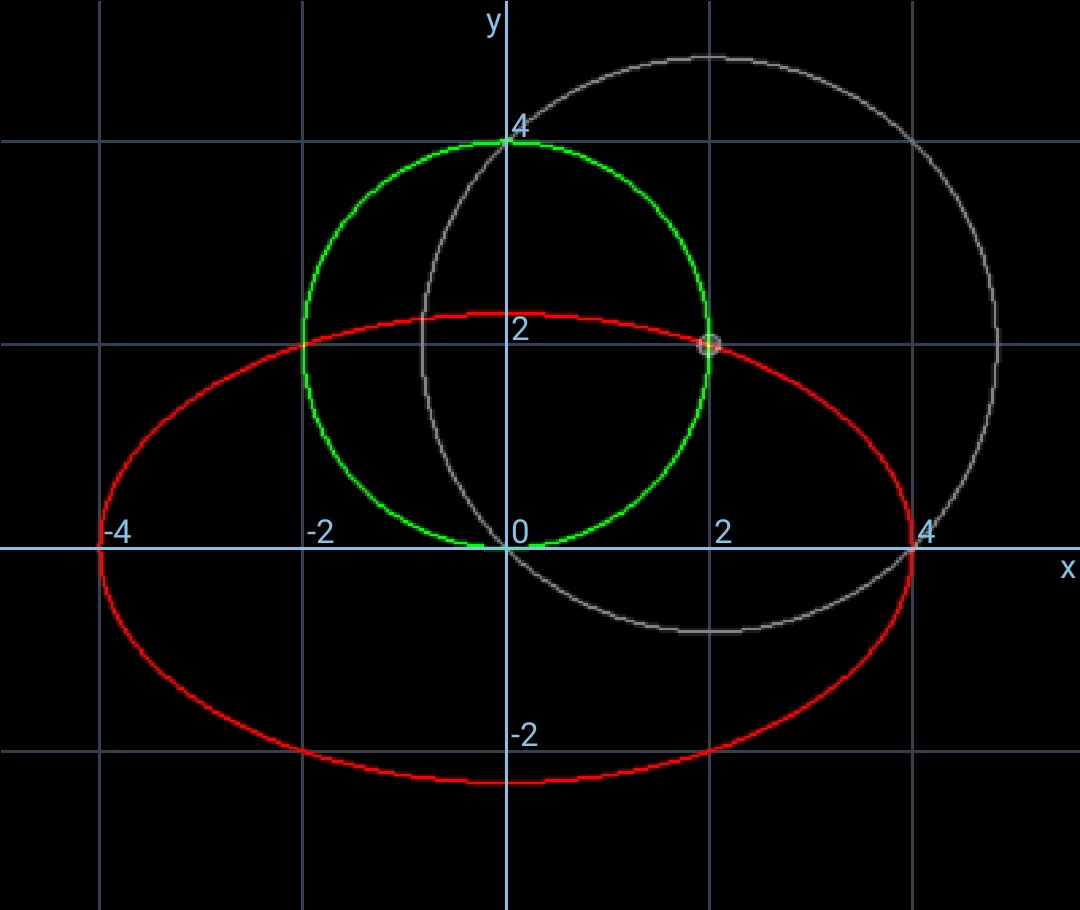
$${A}\left({a},\mathrm{0}\right) \\ $$$${B}\left(\mathrm{0},\mathrm{2}{r}\right) \\ $$$${P}\left(\frac{{a}}{\mathrm{2}},{r}\right) \\ $$$${r}=\frac{{a}}{\mathrm{2}} \\ $$$$\frac{\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow{r}=\frac{\sqrt{\mathrm{3}}{b}}{\mathrm{2}}=\frac{{a}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{{a}}{{b}}=\sqrt{\mathrm{3}} \\ $$$${i}.{e}.\:{possible}\:{only}\:{for}\:{ellipses}\:{with}\:\frac{{a}}{{b}}=\sqrt{\mathrm{3}} \\ $$$${the}\:{radius}\:{is}\:{r}=\frac{{a}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 12/Apr/20
Commented by ajfour last updated on 12/Apr/20

$${Sir},\:{how}\:{P}\:\equiv\left(\frac{{a}}{\mathrm{2}},\:{r}\right)\:\:? \\ $$
Commented by mr W last updated on 12/Apr/20

$${P}\:{is}\:{midpoint}\:{if}\:{AB}, \\ $$$${x}_{{P}} =\frac{{x}_{{A}} +{x}_{{B}} }{\mathrm{2}}=\frac{{a}+\mathrm{0}}{\mathrm{2}}=\frac{{a}}{\mathrm{2}} \\ $$$${y}_{{P}} =\frac{{y}_{{A}} +{y}_{{B}} }{\mathrm{2}}=\frac{\mathrm{0}+\mathrm{2}{r}}{\mathrm{2}}={r} \\ $$
Commented by ajfour last updated on 12/Apr/20

$${why}\:{P}\:{should}\:{be}\:{midpoint}\:{of}\:{AB}, \\ $$$${please}\:{explain}\:{it}\:{Sir},\:{i}\:{dont} \\ $$$${follow}\:\:\left({its}\:{not}\:{given}\:{in}\:{question}\right).. \\ $$
Commented by mr W last updated on 12/Apr/20

$${then}\:{it}'{s}\:{my}\:{misunderstanding}.\:{i} \\ $$$${thought}\:{we}\:{should}\:{find}\:{the}\:{case}\:{with} \\ $$$${AP}={PB}. \\ $$
Answered by mr W last updated on 12/Apr/20
![A(a,0) B(0,2r) say P(a cos θ, b sin θ) P must be on line AB: ((b sin θ)/(a cos θ−a))=((2r)/(−a)) ⇒b sin θ+2r cos θ=2r let μ=(b/a), λ=(r/a) ⇒(r/a)=λ=((μ sin θ)/(2(1−cos θ))) P must be on circle: (a cos θ)^2 +(b sin θ−r)^2 =r^2 (a^2 −b^2 ) sin^2 θ+2br sin θ−a^2 =0 (1−μ^2 )(1−cos^2 θ)+μ^2 (1+cos θ)−1=0 [(1−μ^2 )cos θ−μ^2 ]cos θ=0 ⇒cos θ=0 ⇒ not accepted ⇒cos θ=(μ^2 /(1−μ^2 )) ⇒sin θ=((√(1−2μ^2 ))/(1−μ^2 )) λ=(μ/(2(1−(μ^2 /(1−μ^2 )))))×((√(1−2μ^2 ))/(1−μ^2 )) ⇒λ=(μ/(2(√(1−2μ^2 )))) ⇒r=((ab)/(2(√(a^2 −2b^2 )))) with a>(√2)b](https://www.tinkutara.com/question/Q88694.png)
$${A}\left({a},\mathrm{0}\right) \\ $$$${B}\left(\mathrm{0},\mathrm{2}{r}\right) \\ $$$${say}\:{P}\left({a}\:\mathrm{cos}\:\theta,\:{b}\:\mathrm{sin}\:\theta\right) \\ $$$$ \\ $$$${P}\:{must}\:{be}\:{on}\:{line}\:{AB}: \\ $$$$\frac{{b}\:\mathrm{sin}\:\theta}{{a}\:\mathrm{cos}\:\theta−{a}}=\frac{\mathrm{2}{r}}{−{a}} \\ $$$$\Rightarrow{b}\:\mathrm{sin}\:\theta+\mathrm{2}{r}\:\mathrm{cos}\:\theta=\mathrm{2}{r} \\ $$$${let}\:\mu=\frac{{b}}{{a}},\:\lambda=\frac{{r}}{{a}} \\ $$$$\Rightarrow\frac{{r}}{{a}}=\lambda=\frac{\mu\:\mathrm{sin}\:\theta}{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)} \\ $$$$ \\ $$$${P}\:{must}\:{be}\:{on}\:{circle}: \\ $$$$\left({a}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\left({b}\:\mathrm{sin}\:\theta−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\:\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{2}{br}\:\mathrm{sin}\:\theta−{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)+\mu^{\mathrm{2}} \left(\mathrm{1}+\mathrm{cos}\:\theta\right)−\mathrm{1}=\mathrm{0} \\ $$$$\left[\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{cos}\:\theta−\mu^{\mathrm{2}} \right]\mathrm{cos}\:\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\mathrm{0}\:\Rightarrow\:{not}\:{accepted} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{\mu^{\mathrm{2}} }{\mathrm{1}−\mu^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{\sqrt{\mathrm{1}−\mathrm{2}\mu^{\mathrm{2}} }}{\mathrm{1}−\mu^{\mathrm{2}} } \\ $$$$\lambda=\frac{\mu}{\mathrm{2}\left(\mathrm{1}−\frac{\mu^{\mathrm{2}} }{\mathrm{1}−\mu^{\mathrm{2}} }\right)}×\frac{\sqrt{\mathrm{1}−\mathrm{2}\mu^{\mathrm{2}} }}{\mathrm{1}−\mu^{\mathrm{2}} } \\ $$$$\Rightarrow\lambda=\frac{\mu}{\mathrm{2}\sqrt{\mathrm{1}−\mathrm{2}\mu^{\mathrm{2}} }} \\ $$$$\Rightarrow{r}=\frac{{ab}}{\mathrm{2}\sqrt{{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }}\:\:{with}\:{a}>\sqrt{\mathrm{2}}{b} \\ $$
Commented by mr W last updated on 12/Apr/20

Commented by mr W last updated on 12/Apr/20

Commented by ajfour last updated on 12/Apr/20

$$\mathcal{N}{ice}\:{question},\:{very}\:{nicely} \\ $$$${solved},\:{sir}.\:\mathcal{M}{arvellous},\:{thank}\:{u}. \\ $$
Commented by mr W last updated on 12/Apr/20

$${r}=\frac{{b}}{\mathrm{2}}\:{is}\:{always}\:{a}\:{solution},\:{but}\:{i}\:{think} \\ $$$${we}\:{won}'{t}\:{accept}\:{this},\:{because}\:{B}\:{and}\:{P} \\ $$$${coincide}.\:{otherwise}\:{i}\:{think}\:{for}\: \\ $$$${given}\:{a}\:{and}\:{b},\:{there}\:{is}\:{only}\:{one}\:{value} \\ $$$${for}\:{r}. \\ $$
