Question Number 88967 by ajfour last updated on 14/Apr/20
Commented by ajfour last updated on 14/Apr/20

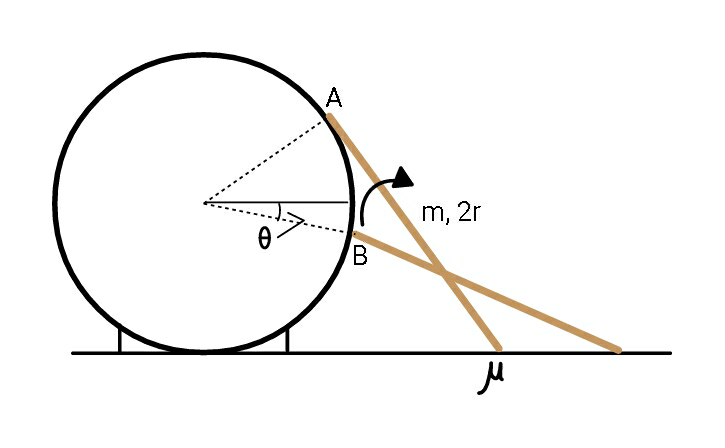
$${A}\:{stick}\:{of}\:{length}\:\mathrm{2}{r}\:{slides}\: \\ $$$${against}\:{a}\:{fixed}\:{smooth}\:{cylindrical} \\ $$$${surface}.\:{It}\:{is}\:{released}\:{with}\:{one} \\ $$$${at}\:{A}\:\left({in}\:{tangential}\:{manner}\right), \\ $$$${and}\:{loses}\:{contact}\:{thereafter}\:{at} \\ $$$${B}.\:{Find}\:\theta.\:{coefficint}\:{of}\:{friction} \\ $$$${between}\:{stick}\:{and}\:{ground}\:{is}\:\mu. \\ $$
Answered by mr W last updated on 14/Apr/20

Commented by mr W last updated on 14/Apr/20
![radius = r length l=2r sin β=((r(1+sin θ))/l)=((1+sin θ)/2) ⇒β=sin^(−1) (((1+sin θ)/2)) at t=0: β=(π/2)−θ_0 sin ((π/2)−θ_0 )=((1+sin θ_0 )/2) 2 cos θ_0 −sin θ_0 =1 ⇒θ_0 =cos^(−1) (1/( (√5)))−cos^(−1) (2/( (√5))) ≈36.87° ϕ=(π/2)−θ φ=tan^(−1) μ (dβ/dθ)=((cos θ)/(2 cos β))=((cos θ)/( (√((1−sin θ)(3+sin θ))))) ω=−(dβ/dt)=−(dβ/dθ)×(dθ/dt)=−((cos θ)/( (√((1−sin θ)(3+sin θ)))))×(dθ/dt) α=(dω/dt)=(dω/dθ)×(dθ/dt)=−((√((1−sin θ)(3+sin θ)))/(cos θ))×((ωdω)/dθ) EB=r cos θ+l cos β=r[cos θ+2(√(1−(((1+sin θ)/2))^2 ))] BC=r+r[cos θ+(√((1−sin θ)(3+sin θ)))]tan θ BC=r[1+sin θ+tan θ(√((1−sin θ)(3+sin θ)))] ((DB)/(sin ϕ))=((BC)/(sin (ϕ+φ))) DB=((r cos θ[1+sin θ+tan θ(√((1−sin θ)(3+sin θ)))])/(cos (θ−φ))) DB=((r[1+sin θ+tan θ(√((1−sin θ)(3+sin θ)))])/(cos φ+tan θ sin φ)) I=((m(2r)^2 )/(12))=((mr^2 )/3) Iα=mg(((l cos β)/2)−DB sin φ) −(r/3)×((√((1−sin θ)(3+sin θ)))/(cos θ))×((ωdω)/dθ)=g(((√((1+sin θ)(3+sin θ)))/2)−((1+sin θ+tan θ(√((1−sin θ)(3+sin θ))))/(cot φ+tan θ))) ((ωdω)/dθ)=−((3g)/r)(((√((1+sin θ)(3+sin θ)))/2)−((1+sin θ+tan θ(√((1−sin θ)(3+sin θ))))/(cot φ+tan θ)))((cos θ)/( (√((1−sin θ)(3+sin θ))))) ((ωdω)/dθ)=−((3g)/r)[((cos θ)/2)−((sin θ)/(cot φ+tan θ))−(((1+sin θ)cos θ)/((cot φ+tan θ)(√((1−sin θ)(3+sin θ)))))] (ω^2 /2)=−((3g)/r)∫_θ_0 ^θ [((cos θ)/2)−((sin θ)/(cot φ+tan θ))−(((1+sin θ)cos θ)/((cot φ+tan θ)(√((1−sin θ)(3+sin θ)))))]dθ ω^2 =−((6g)/r)∫_θ_0 ^θ [((cos θ)/2)−((sin θ)/(cot φ+tan θ))−(((1+sin θ)cos θ)/((cot φ+tan θ)(√((1−sin θ)(3+sin θ)))))]dθ ......](https://www.tinkutara.com/question/Q88989.png)
$${radius}\:=\:{r} \\ $$$${length}\:{l}=\mathrm{2}{r} \\ $$$$\mathrm{sin}\:\beta=\frac{{r}\left(\mathrm{1}+\mathrm{sin}\:\theta\right)}{{l}}=\frac{\mathrm{1}+\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$$\Rightarrow\beta=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}+\mathrm{sin}\:\theta}{\mathrm{2}}\right) \\ $$$${at}\:{t}=\mathrm{0}:\:\beta=\frac{\pi}{\mathrm{2}}−\theta_{\mathrm{0}} \\ $$$$\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\theta_{\mathrm{0}} \right)=\frac{\mathrm{1}+\mathrm{sin}\:\theta_{\mathrm{0}} }{\mathrm{2}} \\ $$$$\mathrm{2}\:\mathrm{cos}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta_{\mathrm{0}} =\mathrm{1} \\ $$$$\Rightarrow\theta_{\mathrm{0}} =\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}−\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\approx\mathrm{36}.\mathrm{87}° \\ $$$$\varphi=\frac{\pi}{\mathrm{2}}−\theta \\ $$$$\phi=\mathrm{tan}^{−\mathrm{1}} \mu \\ $$$$ \\ $$$$\:\frac{{d}\beta}{{d}\theta}=\frac{\mathrm{cos}\:\theta}{\mathrm{2}\:\mathrm{cos}\:\beta}=\frac{\mathrm{cos}\:\theta}{\:\sqrt{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\left(\mathrm{3}+\mathrm{sin}\:\theta\right)}} \\ $$$$\omega=−\frac{{d}\beta}{{dt}}=−\frac{{d}\beta}{{d}\theta}×\frac{{d}\theta}{{dt}}=−\frac{\mathrm{cos}\:\theta}{\:\sqrt{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\left(\mathrm{3}+\mathrm{sin}\:\theta\right)}}×\frac{{d}\theta}{{dt}} \\ $$$$\alpha=\frac{{d}\omega}{{dt}}=\frac{{d}\omega}{{d}\theta}×\frac{{d}\theta}{{dt}}=−\frac{\sqrt{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\left(\mathrm{3}+\mathrm{sin}\:\theta\right)}}{\mathrm{cos}\:\theta}×\frac{\omega{d}\omega}{{d}\theta} \\ $$$${EB}={r}\:\mathrm{cos}\:\theta+{l}\:\mathrm{cos}\:\beta={r}\left[\mathrm{cos}\:\theta+\mathrm{2}\sqrt{\mathrm{1}−\left(\frac{\mathrm{1}+\mathrm{sin}\:\theta}{\mathrm{2}}\right)^{\mathrm{2}} }\right] \\ $$$${BC}={r}+{r}\left[\mathrm{cos}\:\theta+\sqrt{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\left(\mathrm{3}+\mathrm{sin}\:\theta\right)}\right]\mathrm{tan}\:\theta \\ $$$${BC}={r}\left[\mathrm{1}+\mathrm{sin}\:\theta+\mathrm{tan}\:\theta\sqrt{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\left(\mathrm{3}+\mathrm{sin}\:\theta\right)}\right] \\ $$$$\frac{{DB}}{\mathrm{sin}\:\varphi}=\frac{{BC}}{\mathrm{sin}\:\left(\varphi+\phi\right)} \\ $$$${DB}=\frac{{r}\:\mathrm{cos}\:\theta\left[\mathrm{1}+\mathrm{sin}\:\theta+\mathrm{tan}\:\theta\sqrt{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\left(\mathrm{3}+\mathrm{sin}\:\theta\right)}\right]}{\mathrm{cos}\:\left(\theta−\phi\right)} \\ $$$${DB}=\frac{{r}\left[\mathrm{1}+\mathrm{sin}\:\theta+\mathrm{tan}\:\theta\sqrt{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\left(\mathrm{3}+\mathrm{sin}\:\theta\right)}\right]}{\mathrm{cos}\:\phi+\mathrm{tan}\:\theta\:\mathrm{sin}\:\phi} \\ $$$${I}=\frac{{m}\left(\mathrm{2}{r}\right)^{\mathrm{2}} }{\mathrm{12}}=\frac{{mr}^{\mathrm{2}} }{\mathrm{3}} \\ $$$${I}\alpha={mg}\left(\frac{{l}\:\mathrm{cos}\:\beta}{\mathrm{2}}−{DB}\:\mathrm{sin}\:\phi\right) \\ $$$$−\frac{{r}}{\mathrm{3}}×\frac{\sqrt{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\left(\mathrm{3}+\mathrm{sin}\:\theta\right)}}{\mathrm{cos}\:\theta}×\frac{\omega{d}\omega}{{d}\theta}={g}\left(\frac{\sqrt{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\left(\mathrm{3}+\mathrm{sin}\:\theta\right)}}{\mathrm{2}}−\frac{\mathrm{1}+\mathrm{sin}\:\theta+\mathrm{tan}\:\theta\sqrt{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\left(\mathrm{3}+\mathrm{sin}\:\theta\right)}}{\mathrm{cot}\:\phi+\mathrm{tan}\:\theta}\right) \\ $$$$\frac{\omega{d}\omega}{{d}\theta}=−\frac{\mathrm{3}{g}}{{r}}\left(\frac{\sqrt{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\left(\mathrm{3}+\mathrm{sin}\:\theta\right)}}{\mathrm{2}}−\frac{\mathrm{1}+\mathrm{sin}\:\theta+\mathrm{tan}\:\theta\sqrt{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\left(\mathrm{3}+\mathrm{sin}\:\theta\right)}}{\mathrm{cot}\:\phi+\mathrm{tan}\:\theta}\right)\frac{\mathrm{cos}\:\theta}{\:\sqrt{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\left(\mathrm{3}+\mathrm{sin}\:\theta\right)}} \\ $$$$\frac{\omega{d}\omega}{{d}\theta}=−\frac{\mathrm{3}{g}}{{r}}\left[\frac{\mathrm{cos}\:\theta}{\mathrm{2}}−\frac{\mathrm{sin}\:\theta}{\mathrm{cot}\:\phi+\mathrm{tan}\:\theta}−\frac{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\mathrm{cos}\:\theta}{\left(\mathrm{cot}\:\phi+\mathrm{tan}\:\theta\right)\sqrt{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\left(\mathrm{3}+\mathrm{sin}\:\theta\right)}}\right] \\ $$$$\frac{\omega^{\mathrm{2}} }{\mathrm{2}}=−\frac{\mathrm{3}{g}}{{r}}\int_{\theta_{\mathrm{0}} } ^{\theta} \left[\frac{\mathrm{cos}\:\theta}{\mathrm{2}}−\frac{\mathrm{sin}\:\theta}{\mathrm{cot}\:\phi+\mathrm{tan}\:\theta}−\frac{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\mathrm{cos}\:\theta}{\left(\mathrm{cot}\:\phi+\mathrm{tan}\:\theta\right)\sqrt{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\left(\mathrm{3}+\mathrm{sin}\:\theta\right)}}\right]{d}\theta \\ $$$$\omega^{\mathrm{2}} =−\frac{\mathrm{6}{g}}{{r}}\int_{\theta_{\mathrm{0}} } ^{\theta} \left[\frac{\mathrm{cos}\:\theta}{\mathrm{2}}−\frac{\mathrm{sin}\:\theta}{\mathrm{cot}\:\phi+\mathrm{tan}\:\theta}−\frac{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\mathrm{cos}\:\theta}{\left(\mathrm{cot}\:\phi+\mathrm{tan}\:\theta\right)\sqrt{\left(\mathrm{1}−\mathrm{sin}\:\theta\right)\left(\mathrm{3}+\mathrm{sin}\:\theta\right)}}\right]{d}\theta \\ $$$$…… \\ $$
Commented by ajfour last updated on 14/Apr/20
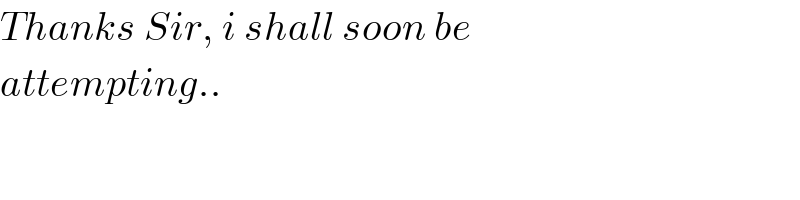
$${Thanks}\:{Sir},\:{i}\:{shall}\:{soon}\:{be} \\ $$$${attempting}.. \\ $$
