Question Number 88997 by jagoll last updated on 14/Apr/20
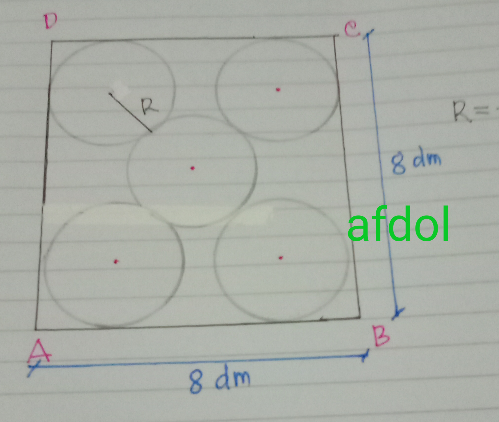
Commented by john santu last updated on 14/Apr/20
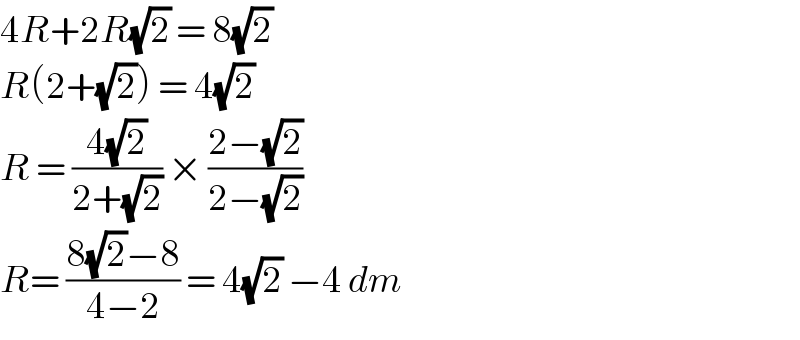
$$\mathrm{4}{R}+\mathrm{2}{R}\sqrt{\mathrm{2}}\:=\:\mathrm{8}\sqrt{\mathrm{2}} \\ $$$${R}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\:=\:\mathrm{4}\sqrt{\mathrm{2}} \\ $$$${R}\:=\:\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\:×\:\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}−\sqrt{\mathrm{2}}}\: \\ $$$${R}=\:\frac{\mathrm{8}\sqrt{\mathrm{2}}−\mathrm{8}}{\mathrm{4}−\mathrm{2}}\:=\:\mathrm{4}\sqrt{\mathrm{2}}\:−\mathrm{4}\:{dm} \\ $$
Commented by mr W last updated on 14/Apr/20

Commented by mr W last updated on 14/Apr/20
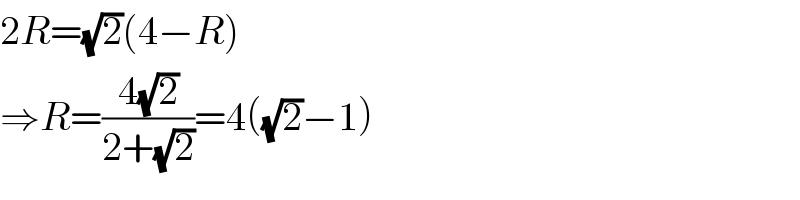
$$\mathrm{2}{R}=\sqrt{\mathrm{2}}\left(\mathrm{4}−{R}\right) \\ $$$$\Rightarrow{R}=\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}=\mathrm{4}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$
Commented by $@ty@m123 last updated on 14/Apr/20

$${Wonderful}!!! \\ $$
Commented by jagoll last updated on 15/Apr/20
$${waw}…….{very}\:{afdoll} \\ $$
