Question Number 89010 by ajfour last updated on 14/Apr/20

Commented by ajfour last updated on 14/Apr/20
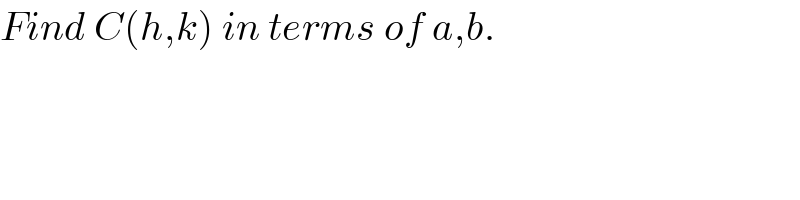
$${Find}\:{C}\left({h},{k}\right)\:{in}\:{terms}\:{of}\:{a},{b}. \\ $$
Commented by ajfour last updated on 14/Apr/20

$${yes}\:{sir},\:{I}\:{agree}. \\ $$
Commented by mr W last updated on 14/Apr/20

$${OD}\:{is}\:{not}\:{independent},\:{so}\:{it}\:{should} \\ $$$${not}\:{be}\:{given}. \\ $$
Commented by ajfour last updated on 15/Apr/20
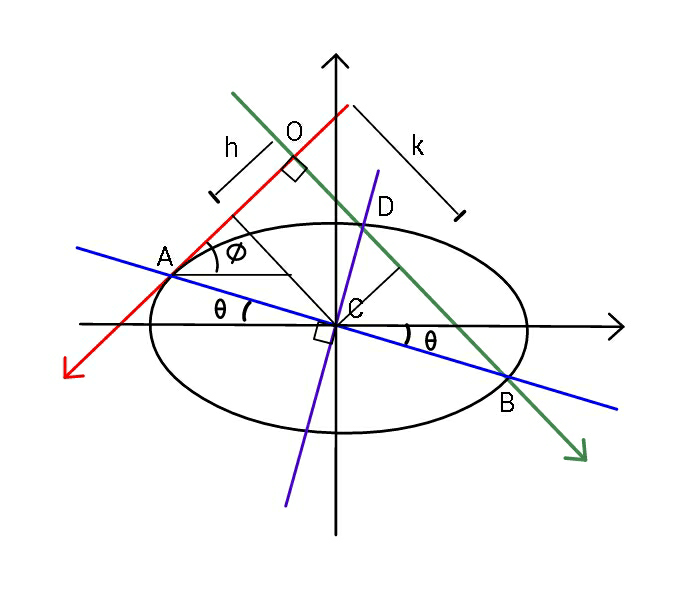
Answered by mr W last updated on 14/Apr/20
Commented by mr W last updated on 16/Apr/20
![let μ=(b/a) ((r^2 cos^2 θ)/a^2 )+((r^2 sin^2 θ)/b^2 )=1 r=((ab)/( (√(a^2 sin^2 θ+b^2 cos^2 θ)))) (x/a^2 )+(y/b^2 )×(dy/dx)=0 ⇒(dy/dx)=−((b^2 x)/(a^2 y))=−(b^2 /(a^2 tan θ)) CA=CB=((ab)/( (√(a^2 sin^2 θ+b^2 cos^2 θ)))) CD=((ab)/( (√(a^2 cos^2 θ+b^2 sin^2 θ)))) tan (ϕ−θ)=(dy/dx)=(b^2 /(a^2 tan θ))=(μ^2 /(tan θ)) ((tan ϕ−tan θ)/(1+tan ϕ tan θ))=(μ^2 /(tan θ)) ⇒tan ϕ=((μ^2 +tan^2 θ)/((1−μ^2 )tan θ)) tan ϕ=((CB)/(CD))=(√((a^2 cos^2 θ+b^2 sin^2 θ)/(a^2 sin^2 θ+b^2 cos^2 θ))) ⇒tan ϕ=(√((1+μ^2 tan^2 θ)/(μ^2 +tan^2 θ))) ((μ^2 +tan^2 θ)/((1−μ^2 )tan θ))=(√((1+μ^2 tan^2 θ)/(μ^2 +tan^2 θ))) ((μ^4 +2μ^2 tan^2 θ+tan^4 θ)/((1−μ^2 )^2 tan^2 θ))=((1+μ^2 tan^2 θ)/(μ^2 +tan^2 θ)) μ^6 +2μ^4 tan^2 θ+μ^2 tan^4 θ+μ^4 tan^2 θ+2μ^2 tan^4 θ+tan^6 θ=(1−μ^2 )^2 tan^2 θ+μ^2 (1−μ^2 )^2 tan^4 θ tan^6 θ+μ^2 (2+2μ^2 −μ^4 )tan^4 θ−(1−2μ^2 −2μ^4 )tan^2 θ+μ^6 =0 (tan^2 θ+1)[tan^4 θ−(1+μ^2 )(1−3μ^2 +μ^4 )tan^2 θ+μ^6 ]=0 ⇒tan^2 θ=(((1+μ^2 )(1−3μ^2 +μ^4 )+(√((1+μ^2 )^2 (1−3μ^2 +μ^4 )^2 −4μ^6 )))/2) ⇒tan θ=(√((1−2μ^2 −2μ^4 +μ^6 +(1−μ^2 )(√(1−2μ^2 −5μ^4 −2μ^6 +μ^8 )))/2))=δ Δ=1−2μ^2 −5μ^4 −2μ^6 +μ^8 ≥0 ⇒μ≤(√((1+2(√2)−(√(5+4(√2))))/2))≈0.531 tan ϕ=((μ^2 +tan^2 θ)/((1−μ^2 )tan θ))=((μ^2 +δ^2 )/((1−μ^2 )δ)) ⇒sin ϕ=((μ^2 +δ^2 )/( (√((1+δ^2 )(μ^4 +δ^2 ))))) x_C =h=CD sin ϕ=((ab sin ϕ)/( (√(a^2 cos^2 θ+b^2 sin^2 θ)))) (h/a)=((μ sin ϕ)/( (√(μ^2 +(1−μ^2 )cos^2 θ)))) ⇒(h/a)=((μ(μ^2 +δ^2 ))/( (√((1+μ^2 δ^2 )(μ^4 +δ^2 ))))) y_C =k=CA sin ϕ=((ab sin ϕ)/( (√(a^2 sin^2 θ+b^2 cos^2 θ)))) (k/a)=((μ sin ϕ)/( (√(1−(1−μ^2 )cos^2 θ)))) ⇒(k/a)=μ(√((μ^2 +δ^2 )/(μ^4 +δ^2 )))](https://www.tinkutara.com/question/Q89027.png)
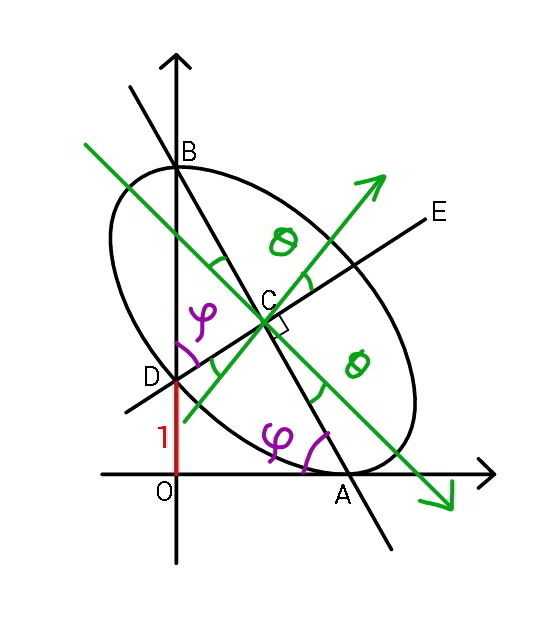
$${let}\:\mu=\frac{{b}}{{a}} \\ $$$$\frac{{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}{{a}^{\mathrm{2}} }+\frac{{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${r}=\frac{{ab}}{\:\sqrt{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}} \\ $$$$\frac{{x}}{{a}^{\mathrm{2}} }+\frac{{y}}{{b}^{\mathrm{2}} }×\frac{{dy}}{{dx}}=\mathrm{0}\:\Rightarrow\frac{{dy}}{{dx}}=−\frac{{b}^{\mathrm{2}} {x}}{{a}^{\mathrm{2}} {y}}=−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} \:\mathrm{tan}\:\theta} \\ $$$$ \\ $$$${CA}={CB}=\frac{{ab}}{\:\sqrt{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}} \\ $$$${CD}=\frac{{ab}}{\:\sqrt{{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$$\mathrm{tan}\:\left(\varphi−\theta\right)=\frac{{dy}}{{dx}}=\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} \:\mathrm{tan}\:\theta}=\frac{\mu^{\mathrm{2}} }{\mathrm{tan}\:\theta} \\ $$$$\frac{\mathrm{tan}\:\varphi−\mathrm{tan}\:\theta}{\mathrm{1}+\mathrm{tan}\:\varphi\:\mathrm{tan}\:\theta}=\frac{\mu^{\mathrm{2}} }{\mathrm{tan}\:\theta} \\ $$$$\Rightarrow\mathrm{tan}\:\varphi=\frac{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}{\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{tan}\:\theta} \\ $$$$ \\ $$$$\mathrm{tan}\:\varphi=\frac{{CB}}{{CD}}=\sqrt{\frac{{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}} \\ $$$$\Rightarrow\mathrm{tan}\:\varphi=\sqrt{\frac{\mathrm{1}+\mu^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta}{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}} \\ $$$$ \\ $$$$\frac{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}{\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{tan}\:\theta}=\sqrt{\frac{\mathrm{1}+\mu^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta}{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}} \\ $$$$\frac{\mu^{\mathrm{4}} +\mathrm{2}\mu^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta+\mathrm{tan}^{\mathrm{4}} \:\theta}{\left(\mathrm{1}−\mu^{\mathrm{2}} \right)^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta}=\frac{\mathrm{1}+\mu^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta}{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta} \\ $$$$\mu^{\mathrm{6}} +\mathrm{2}\mu^{\mathrm{4}} \mathrm{tan}^{\mathrm{2}} \:\theta+\mu^{\mathrm{2}} \mathrm{tan}^{\mathrm{4}} \:\theta+\mu^{\mathrm{4}} \mathrm{tan}^{\mathrm{2}} \:\theta+\mathrm{2}\mu^{\mathrm{2}} \mathrm{tan}^{\mathrm{4}} \:\theta+\mathrm{tan}^{\mathrm{6}} \:\theta=\left(\mathrm{1}−\mu^{\mathrm{2}} \right)^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta+\mu^{\mathrm{2}} \left(\mathrm{1}−\mu^{\mathrm{2}} \right)^{\mathrm{2}} \mathrm{tan}^{\mathrm{4}} \:\theta \\ $$$$\mathrm{tan}^{\mathrm{6}} \:\theta+\mu^{\mathrm{2}} \left(\mathrm{2}+\mathrm{2}\mu^{\mathrm{2}} −\mu^{\mathrm{4}} \right)\mathrm{tan}^{\mathrm{4}} \:\theta−\left(\mathrm{1}−\mathrm{2}\mu^{\mathrm{2}} −\mathrm{2}\mu^{\mathrm{4}} \right)\mathrm{tan}^{\mathrm{2}} \:\theta+\mu^{\mathrm{6}} =\mathrm{0} \\ $$$$\left(\mathrm{tan}^{\mathrm{2}} \:\theta+\mathrm{1}\right)\left[\mathrm{tan}^{\mathrm{4}} \:\theta−\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{3}\mu^{\mathrm{2}} +\mu^{\mathrm{4}} \right)\mathrm{tan}^{\mathrm{2}} \:\theta+\mu^{\mathrm{6}} \right]=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}^{\mathrm{2}} \:\theta=\frac{\left(\mathrm{1}+\mu^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{3}\mu^{\mathrm{2}} +\mu^{\mathrm{4}} \right)+\sqrt{\left(\mathrm{1}+\mu^{\mathrm{2}} \right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{3}\mu^{\mathrm{2}} +\mu^{\mathrm{4}} \right)^{\mathrm{2}} −\mathrm{4}\mu^{\mathrm{6}} }}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\sqrt{\frac{\mathrm{1}−\mathrm{2}\mu^{\mathrm{2}} −\mathrm{2}\mu^{\mathrm{4}} +\mu^{\mathrm{6}} +\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\sqrt{\mathrm{1}−\mathrm{2}\mu^{\mathrm{2}} −\mathrm{5}\mu^{\mathrm{4}} −\mathrm{2}\mu^{\mathrm{6}} +\mu^{\mathrm{8}} }}{\mathrm{2}}}=\delta \\ $$$$\Delta=\mathrm{1}−\mathrm{2}\mu^{\mathrm{2}} −\mathrm{5}\mu^{\mathrm{4}} −\mathrm{2}\mu^{\mathrm{6}} +\mu^{\mathrm{8}} \geqslant\mathrm{0} \\ $$$$\Rightarrow\mu\leqslant\sqrt{\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}−\sqrt{\mathrm{5}+\mathrm{4}\sqrt{\mathrm{2}}}}{\mathrm{2}}}\approx\mathrm{0}.\mathrm{531} \\ $$$$ \\ $$$$\mathrm{tan}\:\varphi=\frac{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}{\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{tan}\:\theta}=\frac{\mu^{\mathrm{2}} +\delta^{\mathrm{2}} }{\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\delta} \\ $$$$\Rightarrow\mathrm{sin}\:\varphi=\frac{\mu^{\mathrm{2}} +\delta^{\mathrm{2}} }{\:\sqrt{\left(\mathrm{1}+\delta^{\mathrm{2}} \right)\left(\mu^{\mathrm{4}} +\delta^{\mathrm{2}} \right)}} \\ $$$$ \\ $$$${x}_{{C}} ={h}={CD}\:\mathrm{sin}\:\varphi=\frac{{ab}\:\mathrm{sin}\:\varphi}{\:\sqrt{{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$$\frac{{h}}{{a}}=\frac{\mu\:\mathrm{sin}\:\varphi}{\:\sqrt{\mu^{\mathrm{2}} +\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta}} \\ $$$$\Rightarrow\frac{{h}}{{a}}=\frac{\mu\left(\mu^{\mathrm{2}} +\delta^{\mathrm{2}} \right)}{\:\sqrt{\left(\mathrm{1}+\mu^{\mathrm{2}} \delta^{\mathrm{2}} \right)\left(\mu^{\mathrm{4}} +\delta^{\mathrm{2}} \right)}} \\ $$$$ \\ $$$${y}_{{C}} ={k}={CA}\:\mathrm{sin}\:\varphi=\frac{{ab}\:\mathrm{sin}\:\varphi}{\:\sqrt{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}} \\ $$$$\frac{{k}}{{a}}=\frac{\mu\:\mathrm{sin}\:\varphi}{\:\sqrt{\mathrm{1}−\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta}} \\ $$$$\Rightarrow\frac{{k}}{{a}}=\mu\sqrt{\frac{\mu^{\mathrm{2}} +\delta^{\mathrm{2}} }{\mu^{\mathrm{4}} +\delta^{\mathrm{2}} }} \\ $$
Commented by mr W last updated on 15/Apr/20
Commented by ajfour last updated on 15/Apr/20

$$\:{Thank}\:{you},\:{Sir}. \\ $$
Commented by mr W last updated on 15/Apr/20
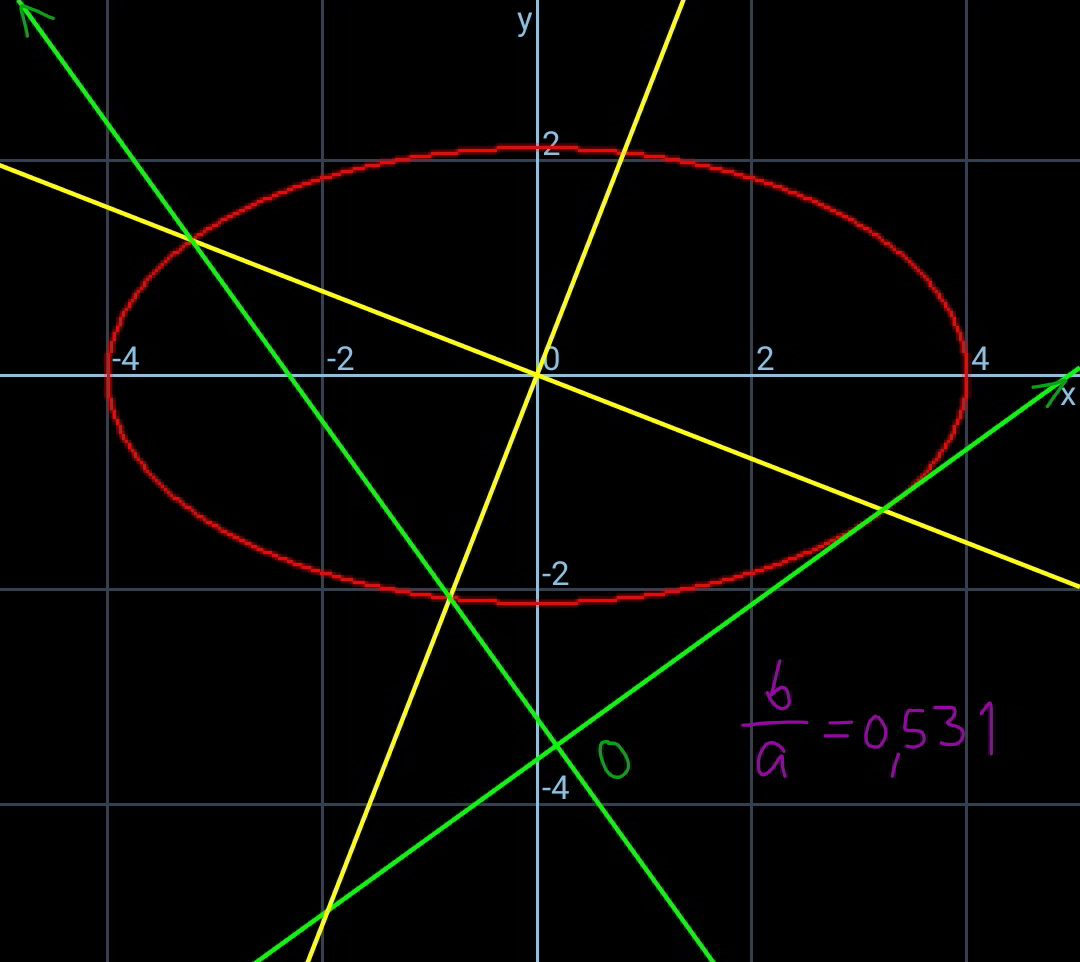
Commented by mr W last updated on 15/Apr/20
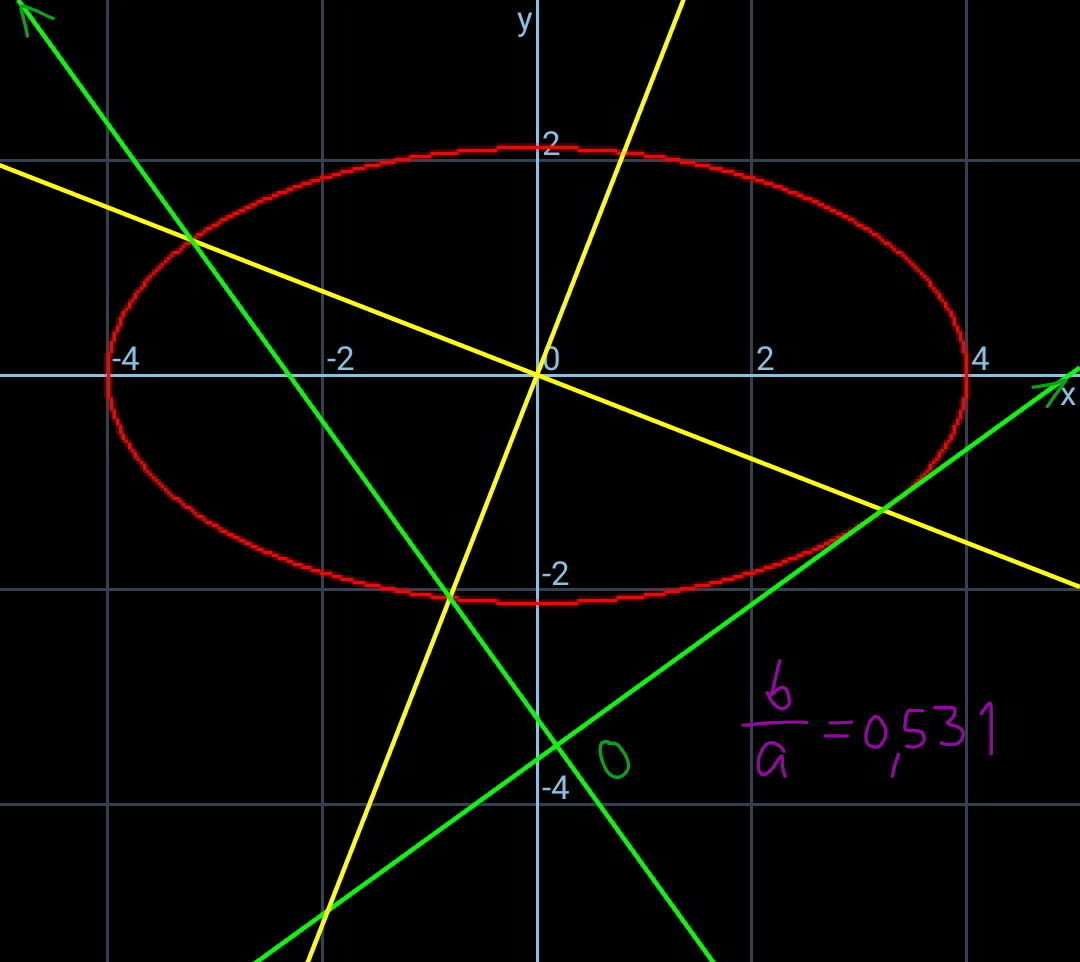
Commented by ajfour last updated on 16/Apr/20
$${Looks},\:{and}\:{indeed},\:{it}\:{is} \\ $$$$\mathcal{BEAUTY}\:\:\mathcal{S}{ir}! \\ $$
Answered by ajfour last updated on 15/Apr/20
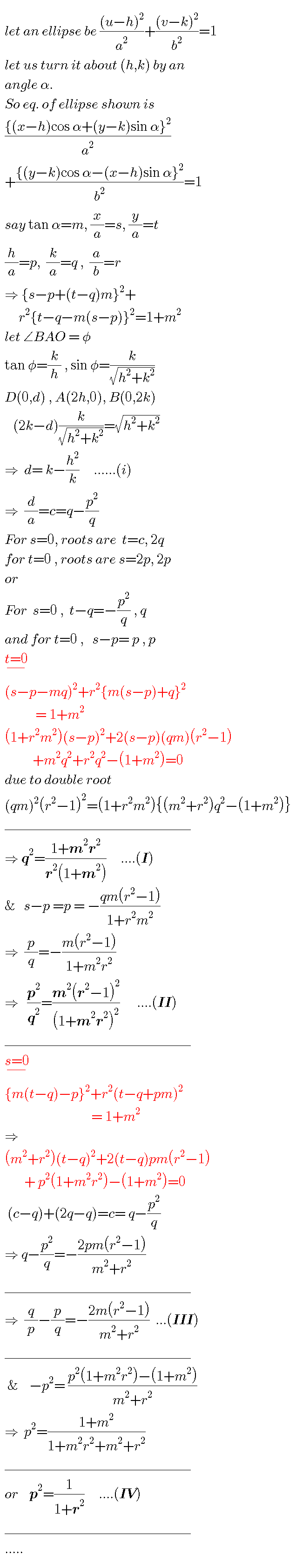
Commented by ajfour last updated on 15/Apr/20

$${sir},\:{something}\:{isn}'{t}\:{just}\:{clear} \\ $$$${to}\:{me}\:{in}\:{this}\:{method}… \\ $$$${I}\:{get}\:\mathrm{4}\:{eqs}.\:\:\:{while}\:{unknowns} \\ $$$${are}\:\:{p},\:{q},\:{m}\:{only}.\:{Please}\: \\ $$$${resolve}\:{my}\:{doubt}\:{Sir}. \\ $$
Commented by mr W last updated on 15/Apr/20

$${i}\:{went}\:{through}\:{your}\:{process}\:{and}\: \\ $$$${could}\:{understand}\:{all}\:{steps}.\:{i}\:{didn}'{t} \\ $$$${see}\:{where}\:{there}\:{is}\:{the}\:{logic}\:{fault}.\:{i}'{ll} \\ $$$${keep}\:{thinking}\:{about}\:{it}. \\ $$
