Question Number 89033 by M±th+et£s last updated on 14/Apr/20

Answered by ajfour last updated on 15/Apr/20
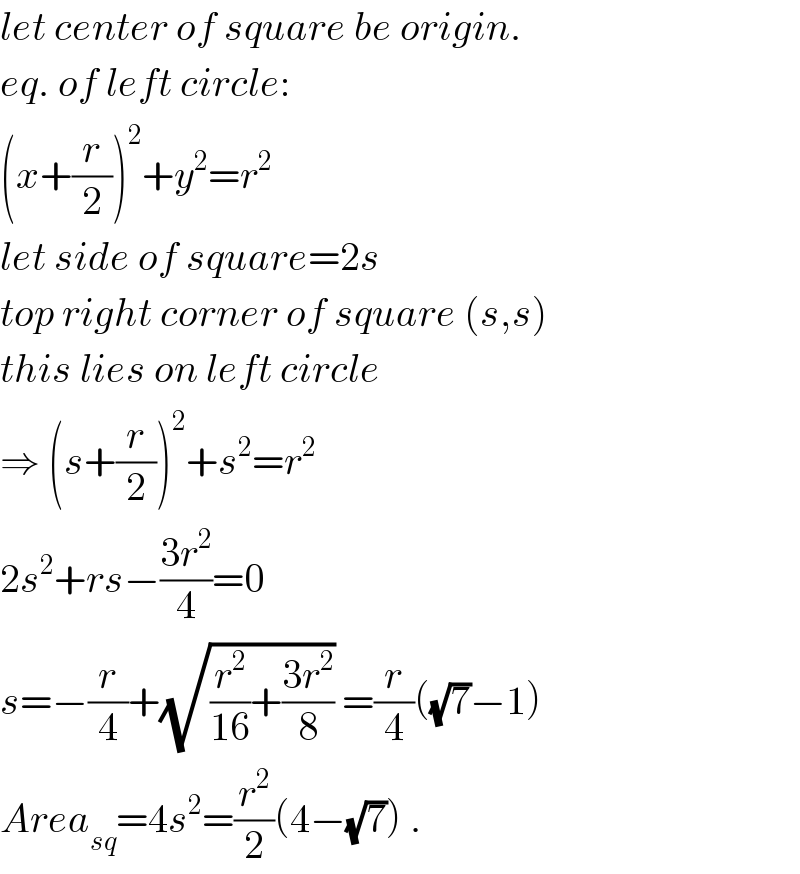
$${let}\:{center}\:{of}\:{square}\:{be}\:{origin}. \\ $$$${eq}.\:{of}\:{left}\:{circle}: \\ $$$$\left({x}+\frac{{r}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${let}\:{side}\:{of}\:{square}=\mathrm{2}{s} \\ $$$${top}\:{right}\:{corner}\:{of}\:{square}\:\left({s},{s}\right) \\ $$$${this}\:{lies}\:{on}\:{left}\:{circle} \\ $$$$\Rightarrow\:\left({s}+\frac{{r}}{\mathrm{2}}\right)^{\mathrm{2}} +{s}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\mathrm{2}{s}^{\mathrm{2}} +{rs}−\frac{\mathrm{3}{r}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0} \\ $$$${s}=−\frac{{r}}{\mathrm{4}}+\sqrt{\frac{{r}^{\mathrm{2}} }{\mathrm{16}}+\frac{\mathrm{3}{r}^{\mathrm{2}} }{\mathrm{8}}}\:=\frac{{r}}{\mathrm{4}}\left(\sqrt{\mathrm{7}}−\mathrm{1}\right) \\ $$$${Area}_{{sq}} =\mathrm{4}{s}^{\mathrm{2}} =\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{4}−\sqrt{\mathrm{7}}\right)\:. \\ $$
Commented by M±th+et£s last updated on 14/Apr/20
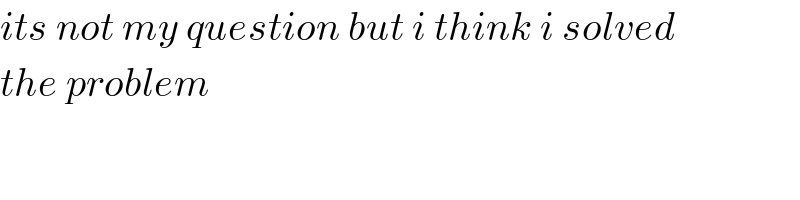
$${its}\:{not}\:{my}\:{question}\:{but}\:{i}\:{think}\:{i}\:{solved} \\ $$$${the}\:{problem}\: \\ $$
Commented by M±th+et£s last updated on 14/Apr/20
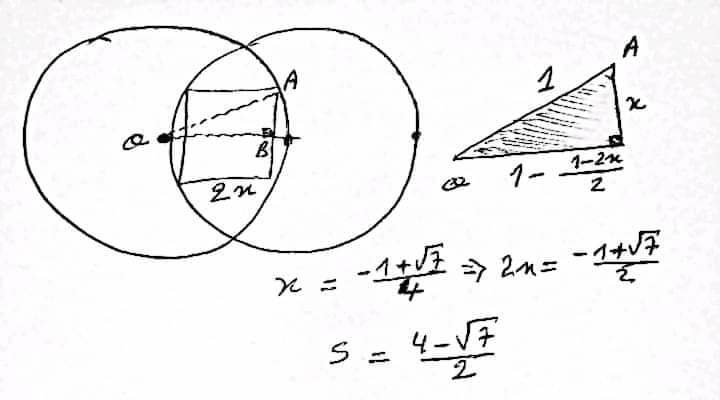
Commented by ajfour last updated on 15/Apr/20
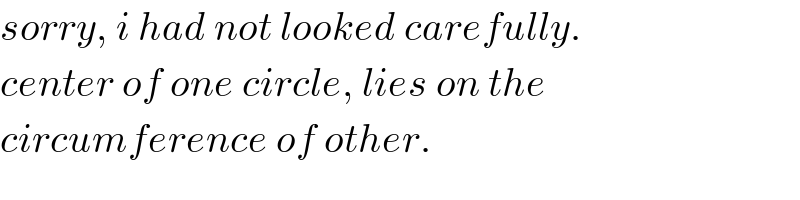
$${sorry},\:{i}\:{had}\:{not}\:{looked}\:{carefully}. \\ $$$${center}\:{of}\:{one}\:{circle},\:{lies}\:{on}\:{the} \\ $$$${circumference}\:{of}\:{other}. \\ $$
Commented by M±th+et£s last updated on 15/Apr/20
$${its}\:{ok}\:{and}\:{thank}\:{you}\:{for}\:{your}\:{try}\: \\ $$
