Menu Close

Question-89124

Tinku Tara 0 Comments
Pin




Question Number 89124 by pete last updated on 15/Apr/20
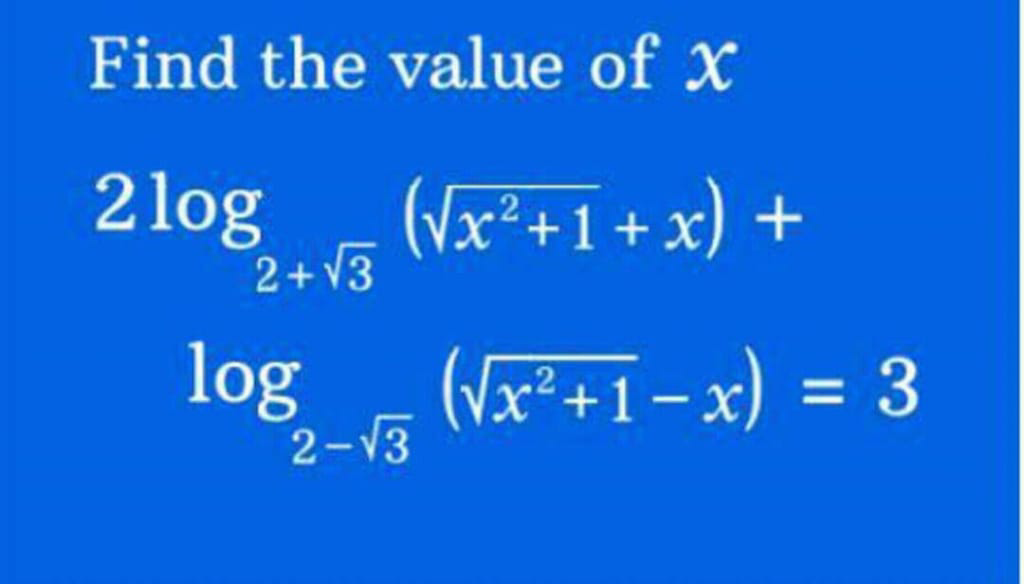
Commented by pete last updated on 15/Apr/20
I need help on this question please
$$\mathrm{I}\:\mathrm{need}\:\mathrm{help}\:\mathrm{on}\:\mathrm{this}\:\mathrm{question}\:\mathrm{please} \\ $$
Commented by john santu last updated on 15/Apr/20
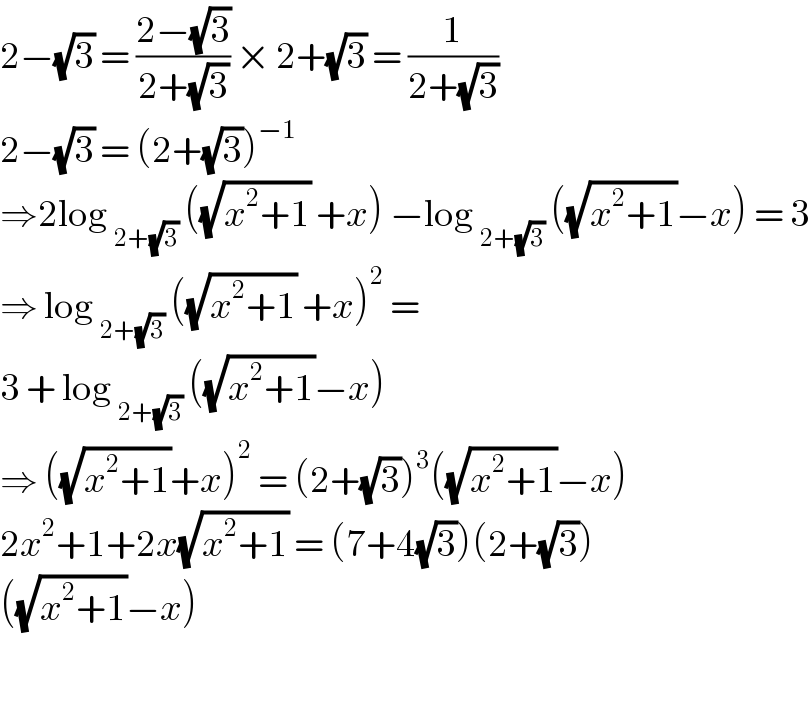
2−(√3) = ((2−(√3))/(2+(√3))) × 2+(√3) = (1/(2+(√3))) 2−(√3) = (2+(√3))^(−1) ⇒2log _(2+(√3)) ((√(x^2 +1)) +x) −log _(2+(√3)) ((√(x^2 +1))−x) = 3 ⇒ log _(2+(√3)) ((√(x^2 +1)) +x)^2 = 3 + log _(2+(√3)) ((√(x^2 +1))−x) ⇒ ((√(x^2 +1))+x)^2 = (2+(√3))^3 ((√(x^2 +1))−x) 2x^2 +1+2x(√(x^2 +1)) = (7+4(√3))(2+(√3)) ((√(x^2 +1))−x)
$$\mathrm{2}−\sqrt{\mathrm{3}}\:=\:\frac{\mathrm{2}−\sqrt{\mathrm{3}}}{\mathrm{2}+\sqrt{\mathrm{3}}}\:×\:\mathrm{2}+\sqrt{\mathrm{3}}\:=\:\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{3}}}\: \\ $$$$\mathrm{2}−\sqrt{\mathrm{3}}\:=\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{−\mathrm{1}} \\ $$$$\Rightarrow\mathrm{2log}\:_{\mathrm{2}+\sqrt{\mathrm{3}}} \:\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:+{x}\right)\:−\mathrm{log}\:_{\mathrm{2}+\sqrt{\mathrm{3}}} \:\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−{x}\right)\:=\:\mathrm{3} \\ $$$$\Rightarrow\:\mathrm{log}\:_{\mathrm{2}+\sqrt{\mathrm{3}}} \:\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:+{x}\right)^{\mathrm{2}} \:=\: \\ $$$$\mathrm{3}\:+\:\mathrm{log}\:_{\mathrm{2}+\sqrt{\mathrm{3}}} \:\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−{x}\right) \\ $$$$\Rightarrow\:\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}+{x}\right)^{\mathrm{2}} \:=\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{3}} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−{x}\right) \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:=\:\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right)\left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$$$\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−{x}\right)\: \\ $$$$ \\ $$
Commented by john santu last updated on 15/Apr/20
my way it standard
$${my}\:{way}\:{it}\:{standard}\: \\ $$
Commented by MJS last updated on 15/Apr/20
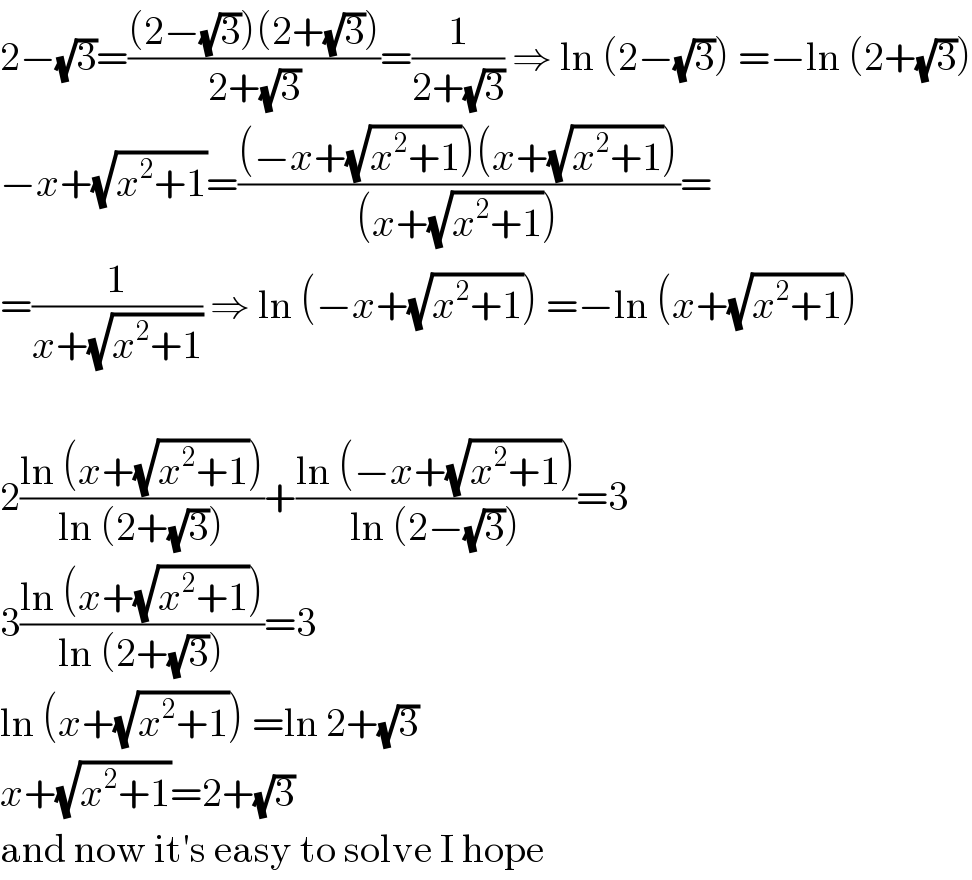
2−(√3)=(((2−(√3))(2+(√3)))/(2+(√3)))=(1/(2+(√3))) ⇒ ln (2−(√3)) =−ln (2+(√3)) −x+(√(x^2 +1))=(((−x+(√(x^2 +1)))(x+(√(x^2 +1))))/((x+(√(x^2 +1)))))= =(1/(x+(√(x^2 +1)))) ⇒ ln (−x+(√(x^2 +1))) =−ln (x+(√(x^2 +1))) 2((ln (x+(√(x^2 +1))))/(ln (2+(√3))))+((ln (−x+(√(x^2 +1))))/(ln (2−(√3))))=3 3((ln (x+(√(x^2 +1))))/(ln (2+(√3))))=3 ln (x+(√(x^2 +1))) =ln 2+(√3) x+(√(x^2 +1))=2+(√3) and now it′s easy to solve I hope
$$\mathrm{2}−\sqrt{\mathrm{3}}=\frac{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)}{\mathrm{2}+\sqrt{\mathrm{3}}}=\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{3}}}\:\Rightarrow\:\mathrm{ln}\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\:=−\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$$$−{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\left(−{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)}{\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)}= \\ $$$$=\frac{\mathrm{1}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\:\Rightarrow\:\mathrm{ln}\:\left(−{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)\:=−\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$$ \\ $$$$\mathrm{2}\frac{\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)}{\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)}+\frac{\mathrm{ln}\:\left(−{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)}{\mathrm{ln}\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)}=\mathrm{3} \\ $$$$\mathrm{3}\frac{\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)}{\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)}=\mathrm{3} \\ $$$$\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)\:=\mathrm{ln}\:\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$${x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$\mathrm{and}\:\mathrm{now}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{I}\:\mathrm{hope} \\ $$
Commented by pete last updated on 16/Apr/20
thanks very much sir
$${thanks}\:{very}\:{much}\:{sir} \\ $$
Answered by MJS last updated on 15/Apr/20
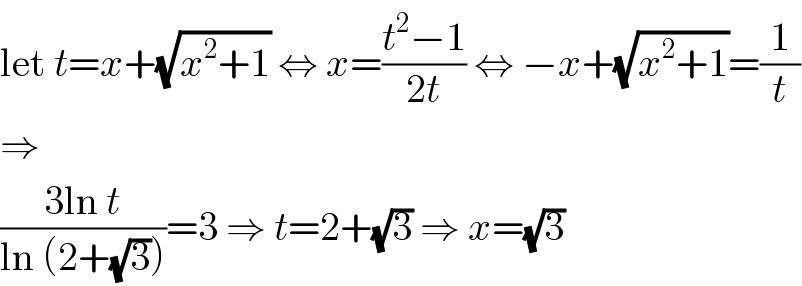
let t=x+(√(x^2 +1)) ⇔ x=((t^2 −1)/(2t)) ⇔ −x+(√(x^2 +1))=(1/t) ⇒ ((3ln t)/(ln (2+(√3))))=3 ⇒ t=2+(√3) ⇒ x=(√3)
$$\mathrm{let}\:{t}={x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\Leftrightarrow\:{x}=\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{t}}\:\Leftrightarrow\:−{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{{t}} \\ $$$$\Rightarrow \\ $$$$\frac{\mathrm{3ln}\:{t}}{\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)}=\mathrm{3}\:\Rightarrow\:{t}=\mathrm{2}+\sqrt{\mathrm{3}}\:\Rightarrow\:{x}=\sqrt{\mathrm{3}} \\ $$
Commented by john santu last updated on 15/Apr/20
only x = (√3) the solution ?
$${only}\:{x}\:=\:\sqrt{\mathrm{3}}\:{the}\:{solution}\:? \\ $$
Commented by MJS last updated on 15/Apr/20
I think so
$$\mathrm{I}\:\mathrm{think}\:\mathrm{so} \\ $$
Commented by john santu last updated on 15/Apr/20
super creative sir
$${super}\:{creative}\:{sir} \\ $$
Commented by pete last updated on 15/Apr/20
i appreciate your time sir, but please kindly elaborate more on in for me to be able to explain it to my students.
$$\mathrm{i}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir},\:\mathrm{but}\:\mathrm{please}\: \\ $$$$\mathrm{kindly}\:\mathrm{elaborate}\:\mathrm{more}\:\mathrm{on}\:\mathrm{in}\:\mathrm{for}\:\mathrm{me}\:\mathrm{to} \\ $$$$\mathrm{be}\:\mathrm{able}\:\mathrm{to}\:\mathrm{explain}\:\mathrm{it}\:\mathrm{to}\:\mathrm{my}\:\mathrm{students}. \\ $$
Answered by Don08q last updated on 22/Jul/20
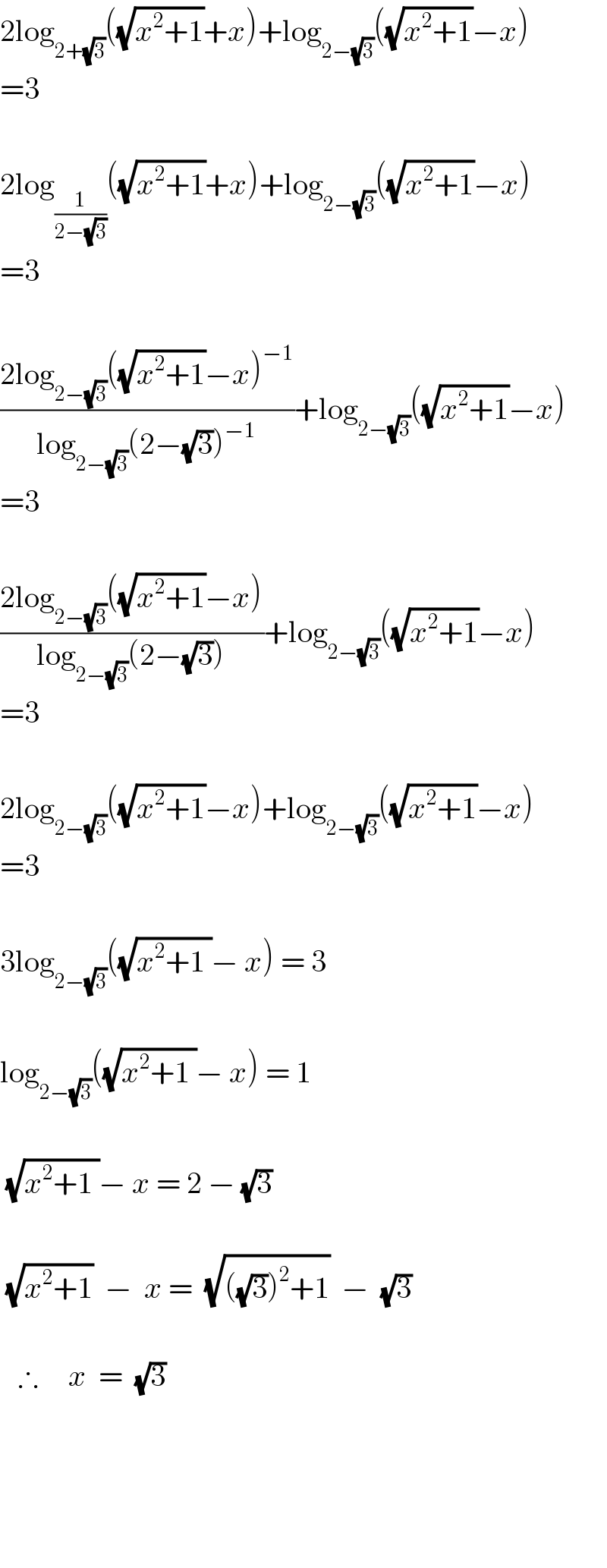
2log_(2+(√3)) ((√(x^2 +1))+x)+log_(2−(√3)) ((√(x^2 +1))−x) =3 2log_(1/(2−(√3))) ((√(x^2 +1))+x)+log_(2−(√3)) ((√(x^2 +1))−x) =3 ((2log_(2−(√3)) ((√(x^2 +1))−x)^(−1) )/(log_(2−(√3)) (2−(√3))^(−1) ))+log_(2−(√3)) ((√(x^2 +1))−x) =3 ((2log_(2−(√3)) ((√(x^2 +1))−x))/(log_(2−(√3)) (2−(√3))))+log_(2−(√3)) ((√(x^2 +1))−x) =3 2log_(2−(√3)) ((√(x^2 +1))−x)+log_(2−(√3)) ((√(x^2 +1))−x) =3 3log_(2−(√3)) ((√(x^2 +1 ))− x) = 3 log_(2−(√3)) ((√(x^2 +1 ))− x) = 1 (√(x^2 +1 ))− x = 2 − (√3) (√(x^2 +1)) − x = (√(((√3))^2 +1)) − (√3) ∴ x = (√3)
$$\mathrm{2log}_{\mathrm{2}+\sqrt{\mathrm{3}}} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}+{x}\right)+\mathrm{log}_{\mathrm{2}−\sqrt{\mathrm{3}}} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−{x}\right)\: \\ $$$$=\mathrm{3} \\ $$$$ \\ $$$$\mathrm{2log}_{\frac{\mathrm{1}}{\mathrm{2}−\sqrt{\mathrm{3}}}} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}+{x}\right)+\mathrm{log}_{\mathrm{2}−\sqrt{\mathrm{3}}} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−{x}\right) \\ $$$$=\mathrm{3} \\ $$$$ \\ $$$$\frac{\mathrm{2log}_{\mathrm{2}−\sqrt{\mathrm{3}}} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−{x}\right)^{−\mathrm{1}} }{\mathrm{log}_{\mathrm{2}−\sqrt{\mathrm{3}}} \left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{−\mathrm{1}} }+\mathrm{log}_{\mathrm{2}−\sqrt{\mathrm{3}}} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−{x}\right) \\ $$$$=\mathrm{3} \\ $$$$ \\ $$$$\frac{\mathrm{2log}_{\mathrm{2}−\sqrt{\mathrm{3}}} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−{x}\right)}{\mathrm{log}_{\mathrm{2}−\sqrt{\mathrm{3}}} \left(\mathrm{2}−\sqrt{\mathrm{3}}\right)}+\mathrm{log}_{\mathrm{2}−\sqrt{\mathrm{3}}} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−{x}\right) \\ $$$$=\mathrm{3} \\ $$$$ \\ $$$$\mathrm{2log}_{\mathrm{2}−\sqrt{\mathrm{3}}} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−{x}\right)+\mathrm{log}_{\mathrm{2}−\sqrt{\mathrm{3}}} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−{x}\right) \\ $$$$=\mathrm{3} \\ $$$$ \\ $$$$\mathrm{3log}_{\mathrm{2}−\sqrt{\mathrm{3}}} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}\:}−\:{x}\right)\:=\:\mathrm{3} \\ $$$$ \\ $$$$\mathrm{log}_{\mathrm{2}−\sqrt{\mathrm{3}}} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}\:}−\:{x}\right)\:=\:\mathrm{1} \\ $$$$ \\ $$$$\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}\:}−\:{x}\:=\:\mathrm{2}\:−\:\sqrt{\mathrm{3}} \\ $$$$ \\ $$$$\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\:−\:\:{x}\:=\:\:\sqrt{\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{1}}\:\:−\:\:\sqrt{\mathrm{3}} \\ $$$$ \\ $$$$\:\:\:\therefore\:\:\:\:\:{x}\:\:=\:\:\sqrt{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *