Question-89187

Question Number 89187 by TawaTawa1 last updated on 16/Apr/20

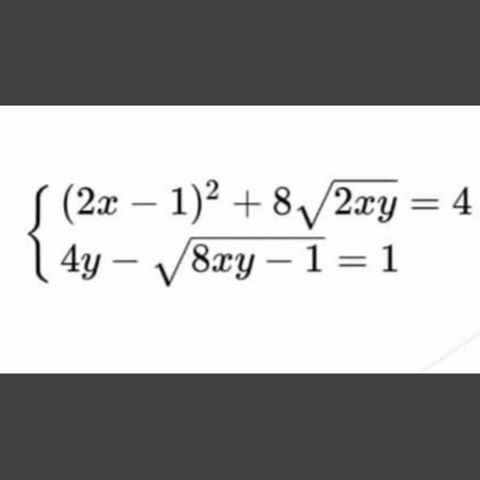
Commented by jagoll last updated on 16/Apr/20

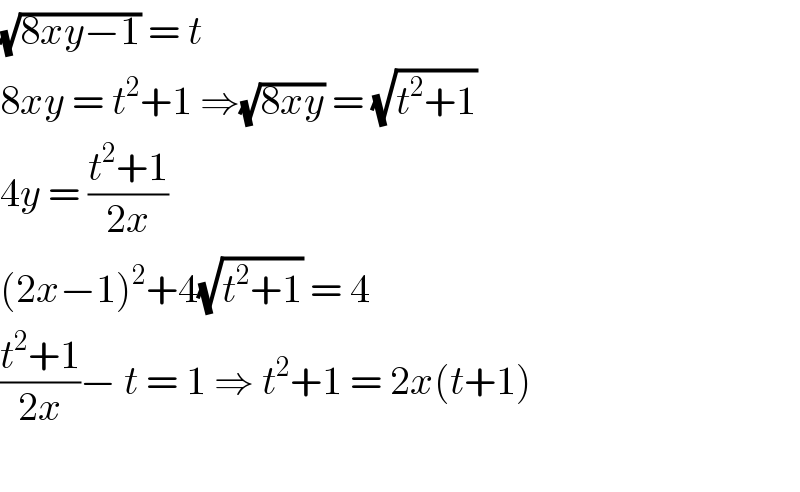
(√(8xy−1)) = t 8xy = t^2 +1 ⇒(√(8xy)) = (√(t^2 +1)) 4y = ((t^2 +1)/(2x)) (2x−1)^2 +4(√(t^2 +1)) = 4 ((t^2 +1)/(2x))− t = 1 ⇒ t^2 +1 = 2x(t+1)

$$\sqrt{\mathrm{8}{xy}−\mathrm{1}}\:=\:{t}\: \\ $$$$\mathrm{8}{xy}\:=\:{t}^{\mathrm{2}} +\mathrm{1}\:\Rightarrow\sqrt{\mathrm{8}{xy}}\:=\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{4}{y}\:=\:\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{x}}\: \\ $$$$\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\:=\:\mathrm{4} \\ $$$$\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{x}}−\:{t}\:=\:\mathrm{1}\:\Rightarrow\:{t}^{\mathrm{2}} +\mathrm{1}\:=\:\mathrm{2}{x}\left({t}+\mathrm{1}\right) \\ $$$$ \\ $$

Commented by jagoll last updated on 16/Apr/20

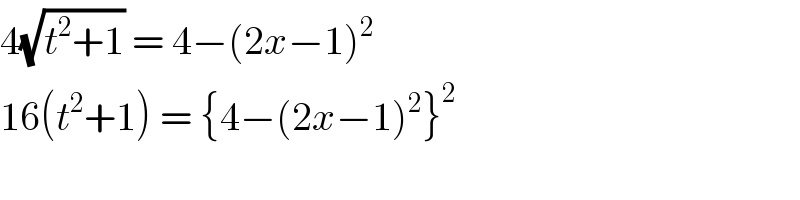
4(√(t^2 +1)) = 4−(2x−1)^2 16(t^2 +1) = {4−(2x−1)^2 }^2

$$\mathrm{4}\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\:=\:\mathrm{4}−\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{16}\left({t}^{\mathrm{2}} +\mathrm{1}\right)\:=\:\left\{\mathrm{4}−\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} \right\}^{\mathrm{2}} \\ $$

Facebook Tweet Pin

Question-89187

Leave a Reply Cancel reply