Question Number 89192 by ajfour last updated on 16/Apr/20

Commented by Prithwish Sen 1 last updated on 16/Apr/20

$$\mathrm{Is}\:\mathrm{E}\:\mathrm{the}\:\mathrm{focus}\:? \\ $$
Commented by ajfour last updated on 16/Apr/20
$${No},\:{nothing}\:{special}. \\ $$
Answered by mr W last updated on 16/Apr/20
![let μ=(b/a) say C(a cos θ, b sin θ) say CA=DE=s s^2 =(1−cos θ)^2 a^2 +sin^2 θ b^2 ((a cos θ)/(b(1+sin θ)))=(b/a) ⇒((cos θ)/(1+sin θ))=μ^2 let t=tan (θ/2) (((1−t^2 )/(1+t^2 ))/(1+((2t)/(1+t^2 ))))=μ^2 ⇒((1−t)/(1+t))=μ^2 ⇒t=((1−μ^2 )/(1+μ^2 )) DE=(b/(b(1+sin θ)))×DC s^2 =(1/((1+sin θ)^2 ))×DC^2 =((b^2 (1+sin θ)^2 +a^2 cos^2 θ)/((1+sin θ)^2 )) s^2 =b^2 +((a^2 cos^2 θ)/((1+sin θ)^2 ))=b^2 +(((1−sin θ)/(1+sin θ)))a^2 b^2 +(((1−sin θ)/(1+sin θ)))a^2 =(1−cos θ)^2 a^2 +sin^2 θ b^2 ⇒((1−sin θ)/(1+sin θ))+2 cos θ−(1−μ^2 )cos^2 θ=1 ((1−((2t)/(1+t^2 )))/(1+((2t)/(1+t^2 ))))+2×((1−t^2 )/(1+t^2 ))−(1−μ^2 )(((1−t^2 )/(1+t^2 )))^2 =1 (((1−t)/(1+t)))^2 +(((1−t^2 )/(1+t^2 )))[2−(1−μ^2 )(((1−t^2 )/(1+t^2 )))]=1 μ^4 +(((1−(((1−μ^2 )/(1+μ^2 )))^2 )/(1+(((1−μ^2 )/(1+μ^2 )))^2 )))[2−(1−μ^2 )(((1−(((1−μ^2 )/(1+μ^2 )))^2 )/(1+(((1−μ^2 )/(1+μ^2 )))^2 )))]=1 μ^4 +(((2μ^2 )/(1+μ^4 )))[2−(1−μ^2 )(((2μ^2 )/(1+μ^4 )))]=1 μ^4 +((4μ^2 (1−μ^2 +2μ^4 ))/((1+μ^4 )^2 ))=1 4μ^2 (1−μ^2 +2μ^4 )=(1−μ^4 )(1+μ^4 )^2 μ^(12) +μ^8 +8μ^6 −5μ^4 +4μ^2 −1=0 ⇒μ≈0.554632](https://www.tinkutara.com/question/Q89225.png)
$${let}\:\mu=\frac{{b}}{{a}} \\ $$$${say}\:{C}\left({a}\:\mathrm{cos}\:\theta,\:{b}\:\mathrm{sin}\:\theta\right) \\ $$$${say}\:{CA}={DE}={s} \\ $$$${s}^{\mathrm{2}} =\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} {a}^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \:\theta\:{b}^{\mathrm{2}} \\ $$$$\frac{{a}\:\mathrm{cos}\:\theta}{{b}\left(\mathrm{1}+\mathrm{sin}\:\theta\right)}=\frac{{b}}{{a}} \\ $$$$\Rightarrow\frac{\mathrm{cos}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta}=\mu^{\mathrm{2}} \\ $$$${let}\:{t}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}} \\ $$$$\frac{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}=\mu^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}=\mu^{\mathrm{2}} \\ $$$$\Rightarrow{t}=\frac{\mathrm{1}−\mu^{\mathrm{2}} }{\mathrm{1}+\mu^{\mathrm{2}} } \\ $$$${DE}=\frac{{b}}{{b}\left(\mathrm{1}+\mathrm{sin}\:\theta\right)}×{DC} \\ $$$${s}^{\mathrm{2}} =\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)^{\mathrm{2}} }×{DC}^{\mathrm{2}} =\frac{{b}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{sin}\:\theta\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)^{\mathrm{2}} } \\ $$$${s}^{\mathrm{2}} ={b}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)^{\mathrm{2}} }={b}^{\mathrm{2}} +\left(\frac{\mathrm{1}−\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta}\right){a}^{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} +\left(\frac{\mathrm{1}−\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta}\right){a}^{\mathrm{2}} =\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} {a}^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \:\theta\:{b}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}−\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta}+\mathrm{2}\:\mathrm{cos}\:\theta−\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\theta=\mathrm{1} \\ $$$$\frac{\mathrm{1}−\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}+\mathrm{2}×\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }−\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\left(\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)\left[\mathrm{2}−\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)\right]=\mathrm{1} \\ $$$$\mu^{\mathrm{4}} +\left(\frac{\mathrm{1}−\left(\frac{\mathrm{1}−\mu^{\mathrm{2}} }{\mathrm{1}+\mu^{\mathrm{2}} }\right)^{\mathrm{2}} }{\mathrm{1}+\left(\frac{\mathrm{1}−\mu^{\mathrm{2}} }{\mathrm{1}+\mu^{\mathrm{2}} }\right)^{\mathrm{2}} }\right)\left[\mathrm{2}−\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\left(\frac{\mathrm{1}−\left(\frac{\mathrm{1}−\mu^{\mathrm{2}} }{\mathrm{1}+\mu^{\mathrm{2}} }\right)^{\mathrm{2}} }{\mathrm{1}+\left(\frac{\mathrm{1}−\mu^{\mathrm{2}} }{\mathrm{1}+\mu^{\mathrm{2}} }\right)^{\mathrm{2}} }\right)\right]=\mathrm{1} \\ $$$$\mu^{\mathrm{4}} +\left(\frac{\mathrm{2}\mu^{\mathrm{2}} }{\mathrm{1}+\mu^{\mathrm{4}} }\right)\left[\mathrm{2}−\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\left(\frac{\mathrm{2}\mu^{\mathrm{2}} }{\mathrm{1}+\mu^{\mathrm{4}} }\right)\right]=\mathrm{1} \\ $$$$\mu^{\mathrm{4}} +\frac{\mathrm{4}\mu^{\mathrm{2}} \left(\mathrm{1}−\mu^{\mathrm{2}} +\mathrm{2}\mu^{\mathrm{4}} \right)}{\left(\mathrm{1}+\mu^{\mathrm{4}} \right)^{\mathrm{2}} }=\mathrm{1} \\ $$$$\mathrm{4}\mu^{\mathrm{2}} \left(\mathrm{1}−\mu^{\mathrm{2}} +\mathrm{2}\mu^{\mathrm{4}} \right)=\left(\mathrm{1}−\mu^{\mathrm{4}} \right)\left(\mathrm{1}+\mu^{\mathrm{4}} \right)^{\mathrm{2}} \\ $$$$\mu^{\mathrm{12}} +\mu^{\mathrm{8}} +\mathrm{8}\mu^{\mathrm{6}} −\mathrm{5}\mu^{\mathrm{4}} +\mathrm{4}\mu^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mu\approx\mathrm{0}.\mathrm{554632} \\ $$
Commented by ajfour last updated on 16/Apr/20

$${Thank}\:{you}\:{Sir}. \\ $$$$\mathcal{N}{ice}\:\mathcal{A}{nswer}\::\:\mu\:\approxeq\:\mathrm{0}.\mathrm{555}\: \\ $$
Commented by mr W last updated on 16/Apr/20
$${you}'{re}\:{right},\:{thanks}! \\ $$
Answered by ajfour last updated on 16/Apr/20
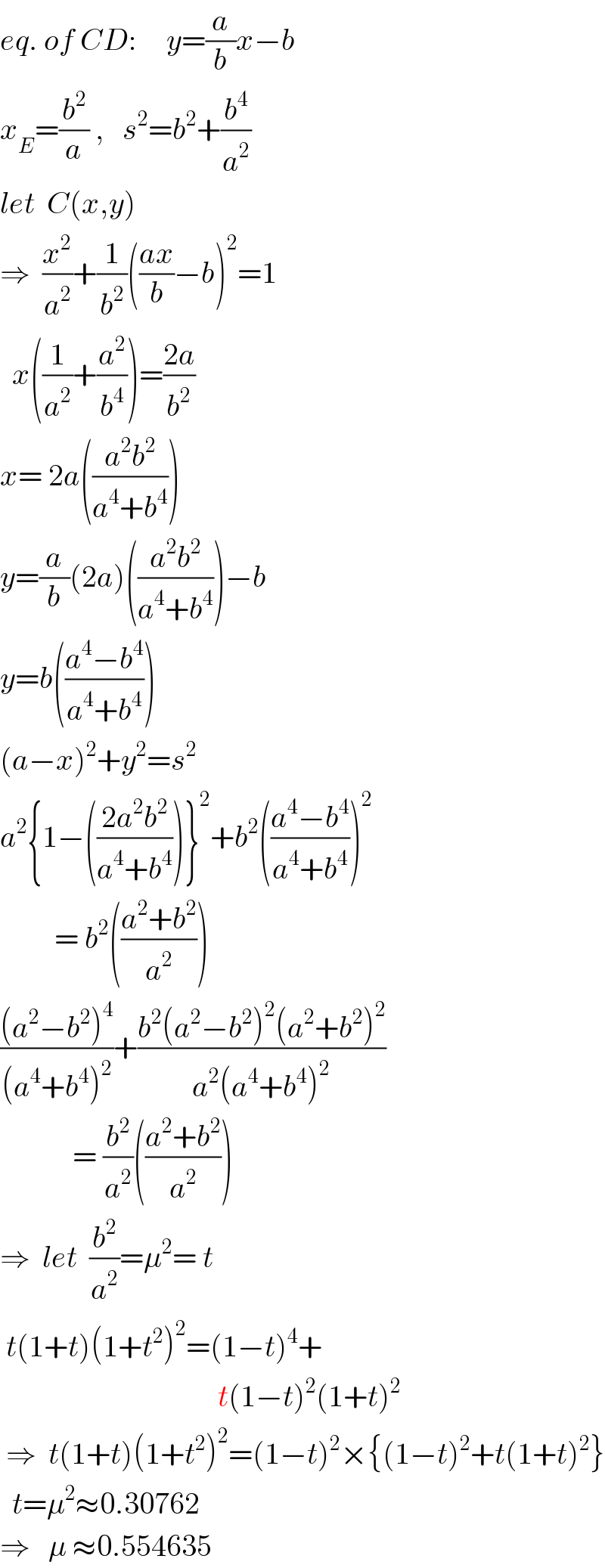
$${eq}.\:{of}\:{CD}:\:\:\:\:\:{y}=\frac{{a}}{{b}}{x}−{b} \\ $$$${x}_{{E}} =\frac{{b}^{\mathrm{2}} }{{a}}\:,\:\:\:{s}^{\mathrm{2}} ={b}^{\mathrm{2}} +\frac{{b}^{\mathrm{4}} }{{a}^{\mathrm{2}} } \\ $$$${let}\:\:{C}\left({x},{y}\right) \\ $$$$\Rightarrow\:\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\left(\frac{{ax}}{{b}}−{b}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\:\:{x}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{4}} }\right)=\frac{\mathrm{2}{a}}{{b}^{\mathrm{2}} } \\ $$$${x}=\:\mathrm{2}{a}\left(\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} }\right)\:\: \\ $$$${y}=\frac{{a}}{{b}}\left(\mathrm{2}{a}\right)\left(\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} }\right)−{b} \\ $$$${y}={b}\left(\frac{{a}^{\mathrm{4}} −{b}^{\mathrm{4}} }{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} }\right) \\ $$$$\left({a}−{x}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} \left\{\mathrm{1}−\left(\frac{\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} }\right)\right\}^{\mathrm{2}} +{b}^{\mathrm{2}} \left(\frac{{a}^{\mathrm{4}} −{b}^{\mathrm{4}} }{{a}^{\mathrm{4}} +{b}^{\mathrm{4}} }\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:=\:{b}^{\mathrm{2}} \left(\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right) \\ $$$$\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{4}} }{\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} \right)^{\mathrm{2}} }+\frac{{b}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} }{{a}^{\mathrm{2}} \left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} \right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\left(\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\:\:{let}\:\:\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }=\mu^{\mathrm{2}} =\:{t} \\ $$$$\:{t}\left(\mathrm{1}+{t}\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} =\left(\mathrm{1}−{t}\right)^{\mathrm{4}} + \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{t}\left(\mathrm{1}−{t}\right)^{\mathrm{2}} \left(\mathrm{1}+{t}\right)^{\mathrm{2}} \\ $$$$\:\Rightarrow\:\:{t}\left(\mathrm{1}+{t}\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} =\left(\mathrm{1}−{t}\right)^{\mathrm{2}} ×\left\{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} +{t}\left(\mathrm{1}+{t}\right)^{\mathrm{2}} \right\} \\ $$$$\:\:{t}=\mu^{\mathrm{2}} \approx\mathrm{0}.\mathrm{30762} \\ $$$$\Rightarrow\:\:\:\mu\:\approx\mathrm{0}.\mathrm{554635} \\ $$
Commented by ajfour last updated on 16/Apr/20

