Menu Close

Question-89194

Tinku Tara 0 Comments
Pin




Question Number 89194 by ajfour last updated on 16/Apr/20
Commented by ajfour last updated on 16/Apr/20
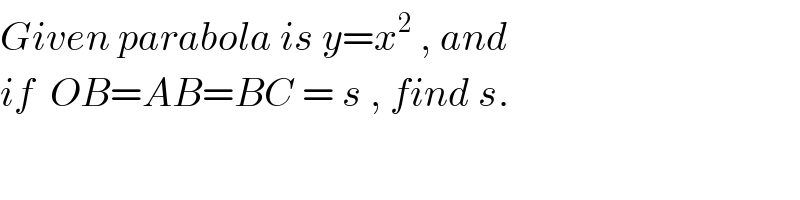
Given parabola is y=x^2 , and if OB=AB=BC = s , find s.
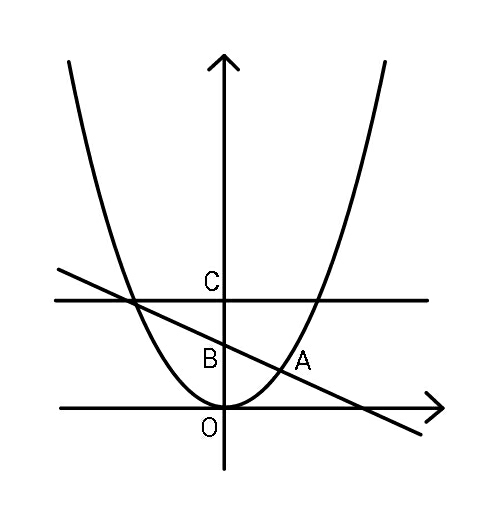
$${Given}\:{parabola}\:{is}\:{y}={x}^{\mathrm{2}} \:,\:{and} \\ $$$${if}\:\:{OB}={AB}={BC}\:=\:{s}\:,\:{find}\:{s}. \\ $$
Commented by john santu last updated on 16/Apr/20
let A(a,a^2 ) , B(0,s) ,C(0,2s) (√(a^2 +(a^2 −s)^2 )) = s a^2 + a^4 −2a^2 s + s^2 = s^2 s = ((a^2 +1)/2). (i) i think the question not complete
$${let}\:{A}\left({a},{a}^{\mathrm{2}} \right)\:,\:{B}\left(\mathrm{0},{s}\right)\:,{C}\left(\mathrm{0},\mathrm{2}{s}\right) \\ $$$$\sqrt{{a}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{s}\right)^{\mathrm{2}} }\:=\:{s}\: \\ $$$${a}^{\mathrm{2}} \:+\:{a}^{\mathrm{4}} −\mathrm{2}{a}^{\mathrm{2}} {s}\:+\:{s}^{\mathrm{2}} \:=\:{s}^{\mathrm{2}} \\ $$$${s}\:=\:\frac{{a}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}}.\:\left({i}\right) \\ $$$${i}\:{think}\:{the}\:{question}\:{not}\:{complete} \\ $$
Answered by mr W last updated on 16/Apr/20
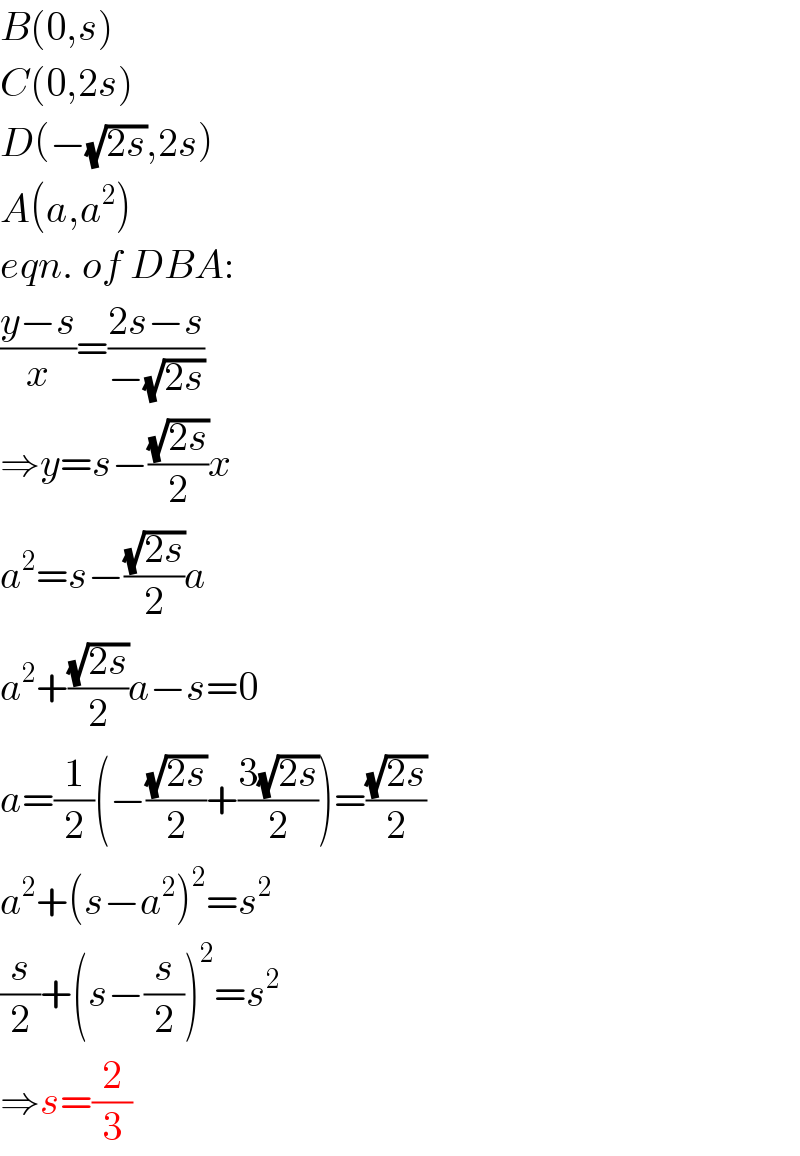
B(0,s) C(0,2s) D(−(√(2s)),2s) A(a,a^2 ) eqn. of DBA: ((y−s)/x)=((2s−s)/(−(√(2s)))) ⇒y=s−((√(2s))/2)x a^2 =s−((√(2s))/2)a a^2 +((√(2s))/2)a−s=0 a=(1/2)(−((√(2s))/2)+((3(√(2s)))/2))=((√(2s))/2) a^2 +(s−a^2 )^2 =s^2 (s/2)+(s−(s/2))^2 =s^2 ⇒s=(2/3)
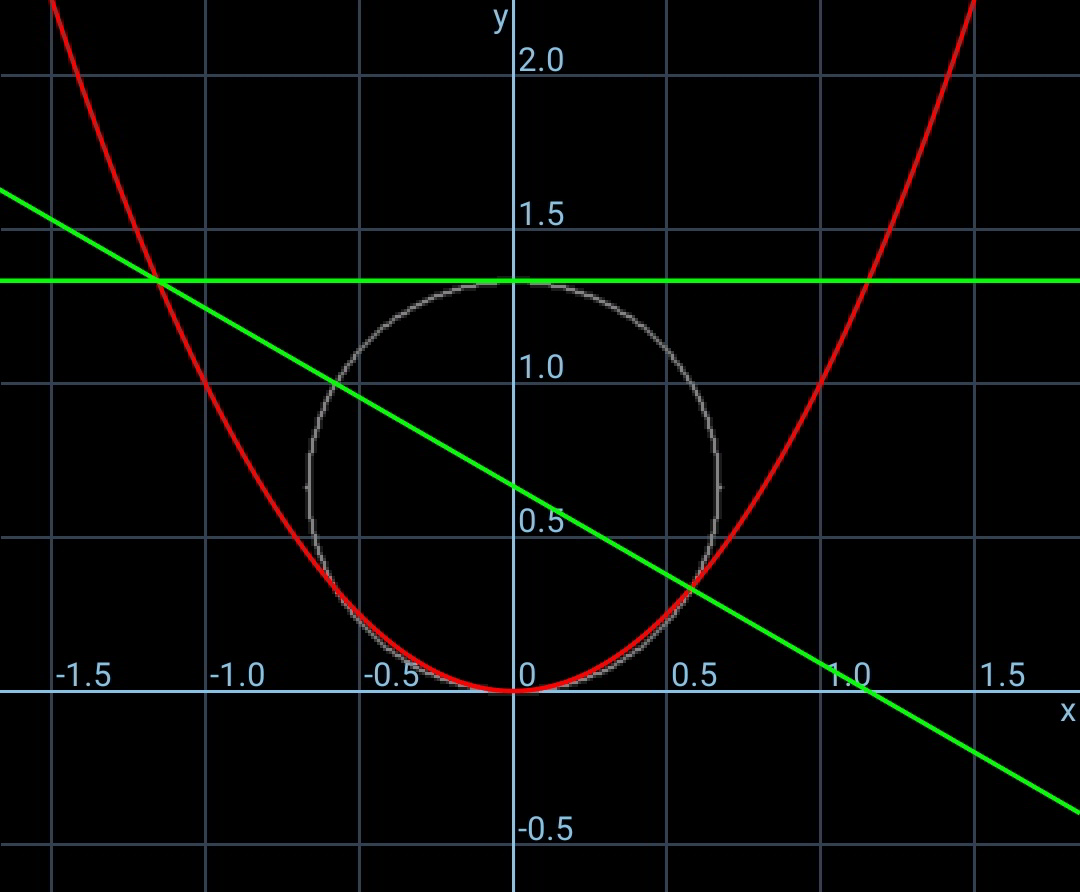
$${B}\left(\mathrm{0},{s}\right) \\ $$$${C}\left(\mathrm{0},\mathrm{2}{s}\right) \\ $$$${D}\left(−\sqrt{\mathrm{2}{s}},\mathrm{2}{s}\right) \\ $$$${A}\left({a},{a}^{\mathrm{2}} \right) \\ $$$${eqn}.\:{of}\:{DBA}: \\ $$$$\frac{{y}−{s}}{{x}}=\frac{\mathrm{2}{s}−{s}}{−\sqrt{\mathrm{2}{s}}} \\ $$$$\Rightarrow{y}={s}−\frac{\sqrt{\mathrm{2}{s}}}{\mathrm{2}}{x} \\ $$$${a}^{\mathrm{2}} ={s}−\frac{\sqrt{\mathrm{2}{s}}}{\mathrm{2}}{a} \\ $$$${a}^{\mathrm{2}} +\frac{\sqrt{\mathrm{2}{s}}}{\mathrm{2}}{a}−{s}=\mathrm{0} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\sqrt{\mathrm{2}{s}}}{\mathrm{2}}+\frac{\mathrm{3}\sqrt{\mathrm{2}{s}}}{\mathrm{2}}\right)=\frac{\sqrt{\mathrm{2}{s}}}{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +\left({s}−{a}^{\mathrm{2}} \right)^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$$\frac{{s}}{\mathrm{2}}+\left({s}−\frac{{s}}{\mathrm{2}}\right)^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$$\Rightarrow{s}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by mr W last updated on 16/Apr/20
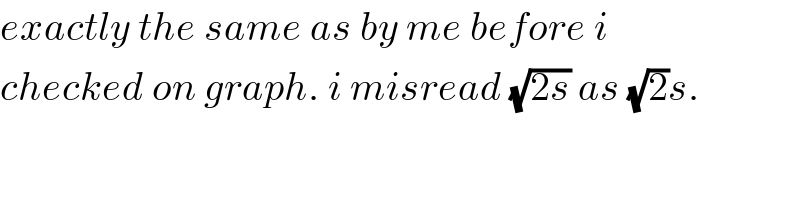
exactly the same as by me before i checked on graph. i misread (√(2s)) as (√2)s.
$${exactly}\:{the}\:{same}\:{as}\:{by}\:{me}\:{before}\:{i} \\ $$$${checked}\:{on}\:{graph}.\:{i}\:{misread}\:\sqrt{\mathrm{2}{s}}\:{as}\:\sqrt{\mathrm{2}}{s}. \\ $$
Commented by ajfour last updated on 16/Apr/20
Correct sir, Perfect!
$${Correct}\:{sir},\:{Perfect}! \\ $$
Commented by mr W last updated on 16/Apr/20
Commented by ajfour last updated on 16/Apr/20
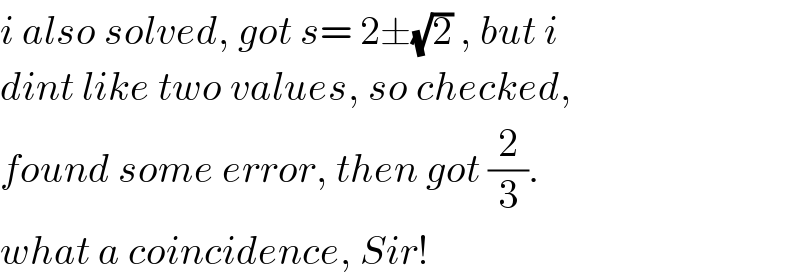
i also solved, got s= 2±(√2) , but i dint like two values, so checked, found some error, then got (2/3). what a coincidence, Sir!
$${i}\:{also}\:{solved},\:{got}\:{s}=\:\mathrm{2}\pm\sqrt{\mathrm{2}}\:,\:{but}\:{i} \\ $$$${dint}\:{like}\:{two}\:{values},\:{so}\:{checked}, \\ $$$${found}\:{some}\:{error},\:{then}\:{got}\:\frac{\mathrm{2}}{\mathrm{3}}. \\ $$$${what}\:{a}\:{coincidence},\:{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *