Question Number 89244 by 174 last updated on 16/Apr/20
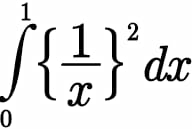
Commented by mathmax by abdo last updated on 16/Apr/20
![A =∫_0 ^1 {(1/x)}^2 dx cha7gement (1/x)=t give A =−∫_1 ^(+∞) {t}^2 (−(dt/t^2 )) =∫_1 ^(+∞) (((t−[t])^2 )/t^2 )dt = ∫_1 ^(+∞) ((t^2 −2t[t]+[t]^2 )/t^2 )dt =∫_1 ^(+∞) (1−2(([t])/t) +(([t]^2 )/t^2 ))dt =Σ_(n=1) ^∞ ∫_n ^(n+1) (1−2(n/t) +(n^2 /t^2 ))dt but ∫_n ^(n+1) (1−2(n/t)+(n^2 /t^2 ))dt =[t−2nln(t)−(n^2 /t)]_n ^(n+1) =1 −2nln(((n+1)/n))−n^2 ((1/(n+1))−(1/n)) =1−2nln(1+(1/n))+(n^2 /(n(n+1))) =1−2nln(1+(1/n))+(n/(n+1)) ln(1+(1/n))∼−2n((1/n)−(1/(2n^2 )))=−2+(1/n^2 ) ⇒ 1−2nln(1+(1/n))+(n/(n+1)) ∼(1/n^2 ) and Σ (1/n^2 ) is convergent....](https://www.tinkutara.com/question/Q89277.png)
$${A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\frac{\mathrm{1}}{{x}}\right\}^{\mathrm{2}} \:{dx}\:\:{cha}\mathrm{7}{gement}\:\frac{\mathrm{1}}{{x}}={t}\:{give}\: \\ $$$${A}\:=−\int_{\mathrm{1}} ^{+\infty} \left\{{t}\right\}^{\mathrm{2}} \left(−\frac{{dt}}{{t}^{\mathrm{2}} }\right)\:=\int_{\mathrm{1}} ^{+\infty} \frac{\left({t}−\left[{t}\right]\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} }{dt} \\ $$$$=\:\int_{\mathrm{1}} ^{+\infty} \:\frac{{t}^{\mathrm{2}} −\mathrm{2}{t}\left[{t}\right]+\left[{t}\right]^{\mathrm{2}} }{{t}^{\mathrm{2}} }{dt}\:=\int_{\mathrm{1}} ^{+\infty} \left(\mathrm{1}−\mathrm{2}\frac{\left[{t}\right]}{{t}}\:+\frac{\left[{t}\right]^{\mathrm{2}} }{{t}^{\mathrm{2}} }\right){dt} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\int_{{n}} ^{{n}+\mathrm{1}} \left(\mathrm{1}−\mathrm{2}\frac{{n}}{{t}}\:+\frac{{n}^{\mathrm{2}} }{{t}^{\mathrm{2}} }\right){dt} \\ $$$${but}\:\int_{{n}} ^{{n}+\mathrm{1}} \left(\mathrm{1}−\mathrm{2}\frac{{n}}{{t}}+\frac{{n}^{\mathrm{2}} }{{t}^{\mathrm{2}} }\right){dt}\:=\left[{t}−\mathrm{2}{nln}\left({t}\right)−\frac{{n}^{\mathrm{2}} }{{t}}\right]_{{n}} ^{{n}+\mathrm{1}} \\ $$$$=\mathrm{1}\:−\mathrm{2}{nln}\left(\frac{{n}+\mathrm{1}}{{n}}\right)−{n}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}}\right) \\ $$$$=\mathrm{1}−\mathrm{2}{nln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)+\frac{{n}^{\mathrm{2}} }{{n}\left({n}+\mathrm{1}\right)}\:=\mathrm{1}−\mathrm{2}{nln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)+\frac{{n}}{{n}+\mathrm{1}} \\ $$$${ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)\sim−\mathrm{2}{n}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }\right)=−\mathrm{2}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{1}−\mathrm{2}{nln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)+\frac{{n}}{{n}+\mathrm{1}}\:\sim\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\:{and}\:\Sigma\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:{is}\:{convergent}…. \\ $$$$ \\ $$
