Question Number 89275 by ajfour last updated on 16/Apr/20
Commented by ajfour last updated on 16/Apr/20

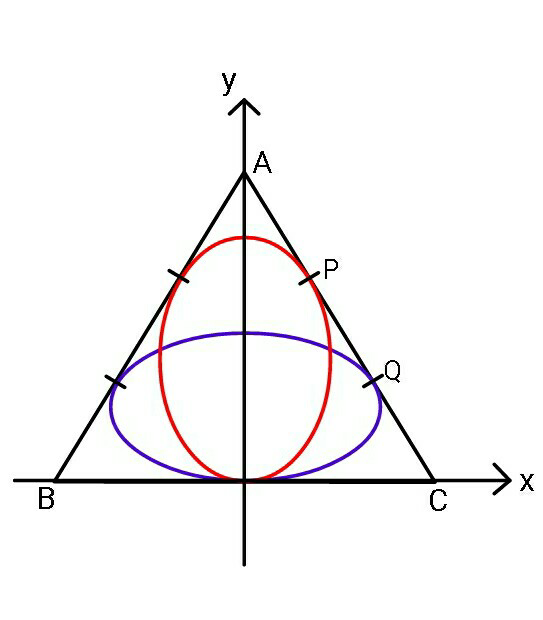
$${If}\:{outer}\:{equilateral}\:{triangle} \\ $$$$\:\:\:\:{has}\:{side}\:{s}=\mathrm{12}\:{units},\:{and}\: \\ $$$$\:\:{AP}\:={PQ}={CQ}\:\:{then}\:{find} \\ $$$${equations}\:{of}\:{both}\:{the}\:{ellipses}. \\ $$
Answered by mr W last updated on 16/Apr/20
![say equation of ellipse is (x^2 /a^2 )+(((y−b)^2 )/b^2 )=1 equation of AC is x+(y/( (√3)))=(s/2) let ((AP)/(AC))=λ P(((λs)/2),(((1−λ)(√3)s)/2)) ((((s/2)−(y/( (√3))))^2 )/a^2 )+(((y−b)^2 )/b^2 )−1=0 (1/a^2 )((s^2 /4)−((sy)/( (√3)))+(y^2 /3))+(1/b^2 )(y^2 −2by+b^2 )−1=0 ((1/(3a^2 ))+(1/b^2 ))y^2 −((s/( (√3)a^2 ))+(2/b))y+(s^2 /(4a^2 ))=0 Δ=((s/( (√3)a^2 ))+(2/b))^2 −4((1/(3a^2 ))+(1/b^2 ))×(s^2 /(4a^2 ))=0 ((s/( (√3)a^2 ))+(2/b))^2 −((1/(3a^2 ))+(1/b^2 ))×(s^2 /a^2 )=0 let μ=(b/a), (s/a)=ξ ⇒((ξ/( (√3)))+(2/μ))^2 =((1/3)+(1/μ^2 ))ξ^2 (((((λs)/2))^2 )/a^2 )+((((((1−λ)(√3)s)/2)−b)^2 )/b^2 )=1 (((λs)^2 )/a^2 )+(([(1−λ)(√3)s−2b]^2 )/b^2 )=4 λ^2 ξ^2 +[(1−λ)(√3)(ξ/μ)−2]^2 =4 λ^2 μ^2 ξ^2 +[(1−λ)(√3)ξ−2μ]^2 =4μ^2 [λ^2 μ^2 +3(1−λ)^2 ]ξ=4(√3)(1−λ)μ ⇒ξ=((4(√3)(1−λ)μ)/(λ^2 μ^2 +3(1−λ)^2 )) ⇒[((4(1−λ)μ)/(λ^2 μ^2 +3(1−λ)^2 ))+(2/μ)]^2 =((1/3)+(1/μ^2 ))[((4(√3)(1−λ)μ)/(λ^2 μ^2 +3(1−λ)^2 ))]^2 [(2−2λ+λ^2 )μ^2 +3(1−λ)^2 ]^2 =4(1−λ)^2 (3+μ^2 )μ^2 ⇒λ^2 (2−λ)^2 μ^4 −6λ(1−λ)^2 (2−λ)μ^2 +9(1−λ)^4 =0 ⇒[λ(2−λ)μ^2 −3(1−λ)^2 ]^2 =0 μ^2 =((3(1−λ)^2 )/(λ(2−λ))) ⇒μ=(b/a)=(1−λ)(√(3/(λ(2−λ)))) ⇒ξ=(s/a)=((4(√3)(1−λ)μ)/(λ^2 μ^2 +3(1−λ)^2 )) for a circle μ=1: (1−λ)(√(3/(λ(2−λ))))=1 4λ^2 −8λ+3=0 ⇒λ=(1/2)](https://www.tinkutara.com/question/Q89287.png)
$${say}\:{equation}\:{of}\:{ellipse}\:{is} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}−{b}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${equation}\:{of}\:{AC}\:{is} \\ $$$${x}+\frac{{y}}{\:\sqrt{\mathrm{3}}}=\frac{{s}}{\mathrm{2}} \\ $$$$ \\ $$$${let}\:\frac{{AP}}{{AC}}=\lambda \\ $$$${P}\left(\frac{\lambda{s}}{\mathrm{2}},\frac{\left(\mathrm{1}−\lambda\right)\sqrt{\mathrm{3}}{s}}{\mathrm{2}}\right) \\ $$$$ \\ $$$$\frac{\left(\frac{{s}}{\mathrm{2}}−\frac{{y}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}−{b}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\mathrm{1}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\left(\frac{{s}^{\mathrm{2}} }{\mathrm{4}}−\frac{{sy}}{\:\sqrt{\mathrm{3}}}+\frac{{y}^{\mathrm{2}} }{\mathrm{3}}\right)+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\left({y}^{\mathrm{2}} −\mathrm{2}{by}+{b}^{\mathrm{2}} \right)−\mathrm{1}=\mathrm{0} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{3}{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right){y}^{\mathrm{2}} −\left(\frac{{s}}{\:\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }+\frac{\mathrm{2}}{{b}}\right){y}+\frac{{s}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Delta=\left(\frac{{s}}{\:\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }+\frac{\mathrm{2}}{{b}}\right)^{\mathrm{2}} −\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{3}{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right)×\frac{{s}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\left(\frac{{s}}{\:\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }+\frac{\mathrm{2}}{{b}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{3}{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right)×\frac{{s}^{\mathrm{2}} }{{a}^{\mathrm{2}} }=\mathrm{0} \\ $$$${let}\:\mu=\frac{{b}}{{a}},\:\frac{{s}}{{a}}=\xi \\ $$$$\Rightarrow\left(\frac{\xi}{\:\sqrt{\mathrm{3}}}+\frac{\mathrm{2}}{\mu}\right)^{\mathrm{2}} =\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mu^{\mathrm{2}} }\right)\xi^{\mathrm{2}} \\ $$$$ \\ $$$$\frac{\left(\frac{\lambda{s}}{\mathrm{2}}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left(\frac{\left(\mathrm{1}−\lambda\right)\sqrt{\mathrm{3}}{s}}{\mathrm{2}}−{b}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{\left(\lambda{s}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left[\left(\mathrm{1}−\lambda\right)\sqrt{\mathrm{3}}{s}−\mathrm{2}{b}\right]^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{4} \\ $$$$\lambda^{\mathrm{2}} \xi^{\mathrm{2}} +\left[\left(\mathrm{1}−\lambda\right)\sqrt{\mathrm{3}}\frac{\xi}{\mu}−\mathrm{2}\right]^{\mathrm{2}} =\mathrm{4} \\ $$$$\lambda^{\mathrm{2}} \mu^{\mathrm{2}} \xi^{\mathrm{2}} +\left[\left(\mathrm{1}−\lambda\right)\sqrt{\mathrm{3}}\xi−\mathrm{2}\mu\right]^{\mathrm{2}} =\mathrm{4}\mu^{\mathrm{2}} \\ $$$$\left[\lambda^{\mathrm{2}} \mu^{\mathrm{2}} +\mathrm{3}\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} \right]\xi=\mathrm{4}\sqrt{\mathrm{3}}\left(\mathrm{1}−\lambda\right)\mu \\ $$$$\Rightarrow\xi=\frac{\mathrm{4}\sqrt{\mathrm{3}}\left(\mathrm{1}−\lambda\right)\mu}{\lambda^{\mathrm{2}} \mu^{\mathrm{2}} +\mathrm{3}\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$\Rightarrow\left[\frac{\mathrm{4}\left(\mathrm{1}−\lambda\right)\mu}{\lambda^{\mathrm{2}} \mu^{\mathrm{2}} +\mathrm{3}\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} }+\frac{\mathrm{2}}{\mu}\right]^{\mathrm{2}} =\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mu^{\mathrm{2}} }\right)\left[\frac{\mathrm{4}\sqrt{\mathrm{3}}\left(\mathrm{1}−\lambda\right)\mu}{\lambda^{\mathrm{2}} \mu^{\mathrm{2}} +\mathrm{3}\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} }\right]^{\mathrm{2}} \\ $$$$\left[\left(\mathrm{2}−\mathrm{2}\lambda+\lambda^{\mathrm{2}} \right)\mu^{\mathrm{2}} +\mathrm{3}\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} \right]^{\mathrm{2}} =\mathrm{4}\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} \left(\mathrm{3}+\mu^{\mathrm{2}} \right)\mu^{\mathrm{2}} \\ $$$$\Rightarrow\lambda^{\mathrm{2}} \left(\mathrm{2}−\lambda\right)^{\mathrm{2}} \mu^{\mathrm{4}} −\mathrm{6}\lambda\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} \left(\mathrm{2}−\lambda\right)\mu^{\mathrm{2}} +\mathrm{9}\left(\mathrm{1}−\lambda\right)^{\mathrm{4}} =\mathrm{0} \\ $$$$\Rightarrow\left[\lambda\left(\mathrm{2}−\lambda\right)\mu^{\mathrm{2}} −\mathrm{3}\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} \right]^{\mathrm{2}} =\mathrm{0} \\ $$$$\mu^{\mathrm{2}} =\frac{\mathrm{3}\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} }{\lambda\left(\mathrm{2}−\lambda\right)} \\ $$$$\Rightarrow\mu=\frac{{b}}{{a}}=\left(\mathrm{1}−\lambda\right)\sqrt{\frac{\mathrm{3}}{\lambda\left(\mathrm{2}−\lambda\right)}} \\ $$$$\Rightarrow\xi=\frac{{s}}{{a}}=\frac{\mathrm{4}\sqrt{\mathrm{3}}\left(\mathrm{1}−\lambda\right)\mu}{\lambda^{\mathrm{2}} \mu^{\mathrm{2}} +\mathrm{3}\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} } \\ $$$$ \\ $$$${for}\:{a}\:{circle}\:\mu=\mathrm{1}: \\ $$$$\left(\mathrm{1}−\lambda\right)\sqrt{\frac{\mathrm{3}}{\lambda\left(\mathrm{2}−\lambda\right)}}=\mathrm{1} \\ $$$$\mathrm{4}\lambda^{\mathrm{2}} −\mathrm{8}\lambda+\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by ajfour last updated on 17/Apr/20
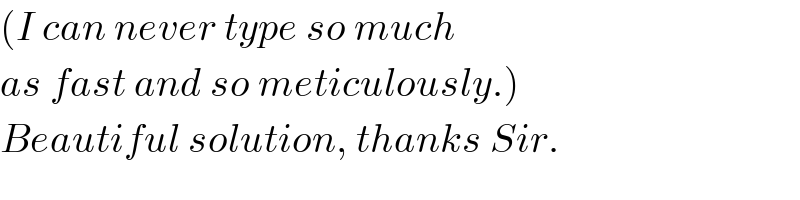
$$\left({I}\:{can}\:{never}\:{type}\:{so}\:{much}\right. \\ $$$$\left.{as}\:{fast}\:{and}\:{so}\:{meticulously}.\right) \\ $$$${Beautiful}\:{solution},\:{thanks}\:{Sir}. \\ $$
Commented by mr W last updated on 16/Apr/20

Commented by mr W last updated on 16/Apr/20

Commented by mr W last updated on 16/Apr/20

Commented by ajfour last updated on 17/Apr/20
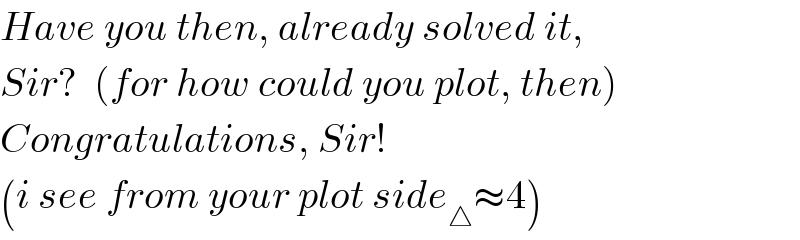
$${Have}\:{you}\:{then},\:{already}\:{solved}\:{it}, \\ $$$${Sir}?\:\:\left({for}\:{how}\:{could}\:{you}\:{plot},\:{then}\right) \\ $$$${Congratulations},\:{Sir}! \\ $$$$\left({i}\:{see}\:{from}\:{your}\:{plot}\:{side}_{\bigtriangleup} \approx\mathrm{4}\right) \\ $$
