Menu Close

Question-89281

Tinku Tara 0 Comments
Pin




Question Number 89281 by ajfour last updated on 16/Apr/20
Commented by ajfour last updated on 17/Apr/20
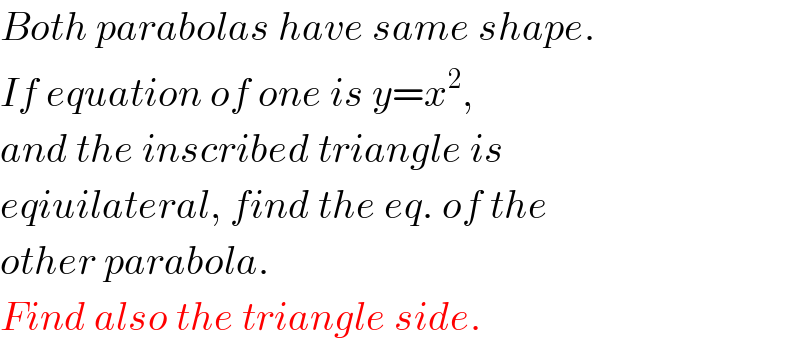
Both parabolas have same shape. If equation of one is y=x^2 , and the inscribed triangle is eqiuilateral, find the eq. of the other parabola. Find also the triangle side.
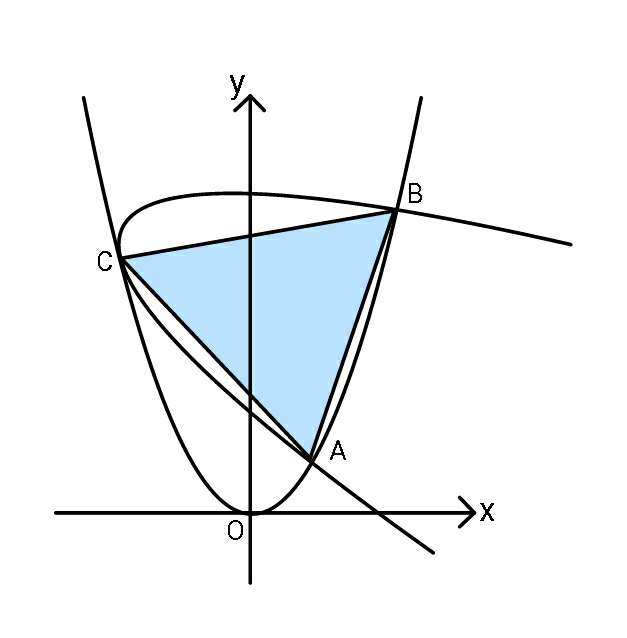
$${Both}\:{parabolas}\:{have}\:{same}\:{shape}. \\ $$$${If}\:{equation}\:{of}\:{one}\:{is}\:{y}={x}^{\mathrm{2}} , \\ $$$${and}\:{the}\:{inscribed}\:{triangle}\:{is} \\ $$$${eqiuilateral},\:{find}\:{the}\:{eq}.\:{of}\:{the} \\ $$$${other}\:{parabola}. \\ $$$${Find}\:{also}\:{the}\:{triangle}\:{side}. \\ $$
Commented by ajfour last updated on 17/Apr/20
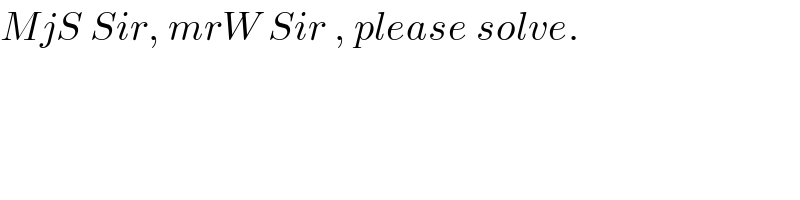
MjS Sir, mrW Sir , please solve.
$${MjS}\:{Sir},\:{mrW}\:{Sir}\:,\:{please}\:{solve}. \\ $$
Answered by mr W last updated on 17/Apr/20
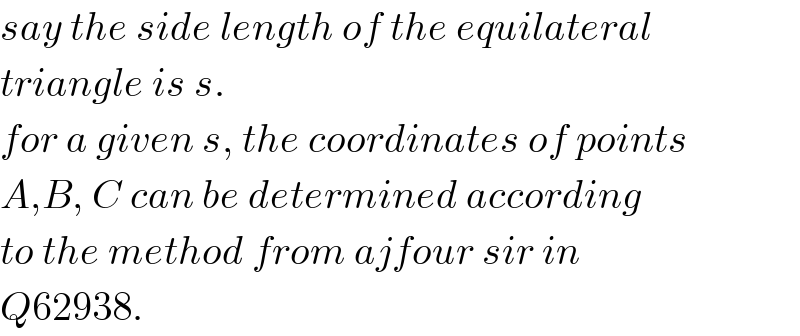
say the side length of the equilateral triangle is s. for a given s, the coordinates of points A,B, C can be determined according to the method from ajfour sir in Q62938.
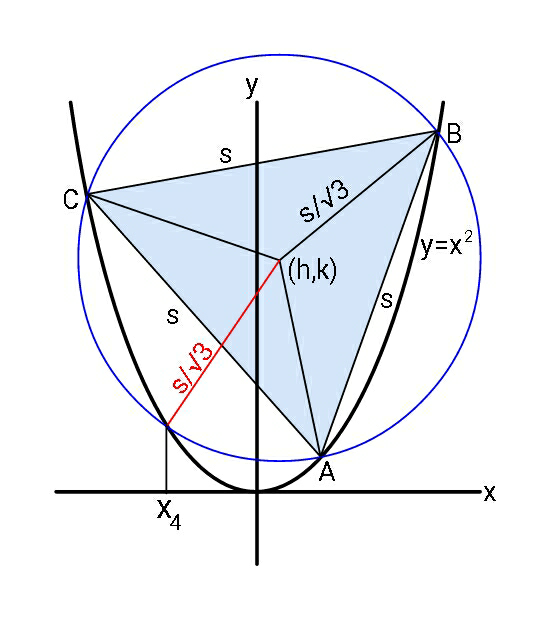
$${say}\:{the}\:{side}\:{length}\:{of}\:{the}\:{equilateral} \\ $$$${triangle}\:{is}\:{s}. \\ $$$${for}\:{a}\:{given}\:{s},\:{the}\:{coordinates}\:{of}\:{points} \\ $$$${A},{B},\:{C}\:{can}\:{be}\:{determined}\:{according} \\ $$$${to}\:{the}\:{method}\:{from}\:{ajfour}\:{sir}\:{in} \\ $$$${Q}\mathrm{62938}. \\ $$
Commented by mr W last updated on 24/Apr/20
coordinates of the centroid G(h,k): h=(√((s^2 /(48))−(1/4))) k=((3s^2 )/(16))−(1/4) (s^2 /(48))−(1/4)≥0 ⇒s≥2(√3) the x−coordinates of points A,B,C can be calculated as roots of following equation: x^3 +ax^2 +bx+c=0 with a=−3h b=(3/2)(3h^2 −k) c=(1/(3h))(h^2 +k^2 −(s^2 /3)) the equation can be reformed to: z^3 +3pz+2q=0 with x=z+h p=((h^2 −k)/2) q=((h(5h^2 −3k))/4)+((3h^2 +3k^2 −s^2 )/(18h)) the roots are x_i =2(√(−p)) sin ((1/3)sin^(−1) (q/( (√(−p^3 ))))+((2iπ)/3))+h (i=0,1,2 for point A,B,C respectively) x_A =x_0 =2(√(−p)) sin ((1/3)sin^(−1) (q/( (√(−p^3 )))))+h x_C =x_2 =2(√(−p)) sin ((1/3)sin^(−1) (q/( (√(−p^3 ))))+((4π)/3))+h
$${coordinates}\:{of}\:{the}\:{centroid}\:{G}\left({h},{k}\right): \\ $$$${h}=\sqrt{\frac{{s}^{\mathrm{2}} }{\mathrm{48}}−\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$${k}=\frac{\mathrm{3}{s}^{\mathrm{2}} }{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\frac{{s}^{\mathrm{2}} }{\mathrm{48}}−\frac{\mathrm{1}}{\mathrm{4}}\geqslant\mathrm{0}\:\Rightarrow\boldsymbol{{s}}\geqslant\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$ \\ $$$${the}\:{x}−{coordinates}\:{of}\:{points}\:{A},{B},{C} \\ $$$${can}\:{be}\:{calculated}\:{as}\:{roots}\:{of}\:{following} \\ $$$${equation}: \\ $$$${x}^{\mathrm{3}} +{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$${with} \\ $$$${a}=−\mathrm{3}{h} \\ $$$${b}=\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{3}{h}^{\mathrm{2}} −{k}\right) \\ $$$${c}=\frac{\mathrm{1}}{\mathrm{3}{h}}\left({h}^{\mathrm{2}} +{k}^{\mathrm{2}} −\frac{{s}^{\mathrm{2}} }{\mathrm{3}}\right) \\ $$$$ \\ $$$${the}\:{equation}\:{can}\:{be}\:{reformed}\:{to}: \\ $$$${z}^{\mathrm{3}} +\mathrm{3}{pz}+\mathrm{2}{q}=\mathrm{0} \\ $$$${with} \\ $$$${x}={z}+{h} \\ $$$${p}=\frac{{h}^{\mathrm{2}} −{k}}{\mathrm{2}} \\ $$$${q}=\frac{{h}\left(\mathrm{5}{h}^{\mathrm{2}} −\mathrm{3}{k}\right)}{\mathrm{4}}+\frac{\mathrm{3}{h}^{\mathrm{2}} +\mathrm{3}{k}^{\mathrm{2}} −{s}^{\mathrm{2}} }{\mathrm{18}{h}} \\ $$$$ \\ $$$${the}\:{roots}\:{are} \\ $$$${x}_{{i}} =\mathrm{2}\sqrt{−{p}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{{q}}{\:\sqrt{−{p}^{\mathrm{3}} }}+\frac{\mathrm{2}{i}\pi}{\mathrm{3}}\right)+{h} \\ $$$$\left({i}=\mathrm{0},\mathrm{1},\mathrm{2}\:{for}\:{point}\:{A},{B},{C}\:{respectively}\right) \\ $$$$ \\ $$$${x}_{{A}} ={x}_{\mathrm{0}} =\mathrm{2}\sqrt{−{p}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{{q}}{\:\sqrt{−{p}^{\mathrm{3}} }}\right)+{h} \\ $$$${x}_{{C}} ={x}_{\mathrm{2}} =\mathrm{2}\sqrt{−{p}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{{q}}{\:\sqrt{−{p}^{\mathrm{3}} }}+\frac{\mathrm{4}\pi}{\mathrm{3}}\right)+{h} \\ $$
Commented by ajfour last updated on 18/Apr/20
Sir, Q.89415 please , can you confirm just the answer..
$${Sir},\:{Q}.\mathrm{89415}\:{please}\:,\:{can}\:{you} \\ $$$${confirm}\:{just}\:{the}\:{answer}.. \\ $$
Commented by mr W last updated on 17/Apr/20
Commented by mr W last updated on 18/Apr/20
this solution was only possible due to your earlier wonderful work. therefore big thanks to you for the question and for the contribution to the solution!
$${this}\:{solution}\:{was}\:{only}\:{possible}\:{due}\:{to} \\ $$$${your}\:{earlier}\:{wonderful}\:{work}.\:{therefore} \\ $$$${big}\:{thanks}\:{to}\:{you}\:{for}\:{the}\:{question}\:{and} \\ $$$${for}\:{the}\:{contribution}\:{to}\:{the}\:{solution}! \\ $$
Commented by mr W last updated on 17/Apr/20
Commented by mr W last updated on 18/Apr/20
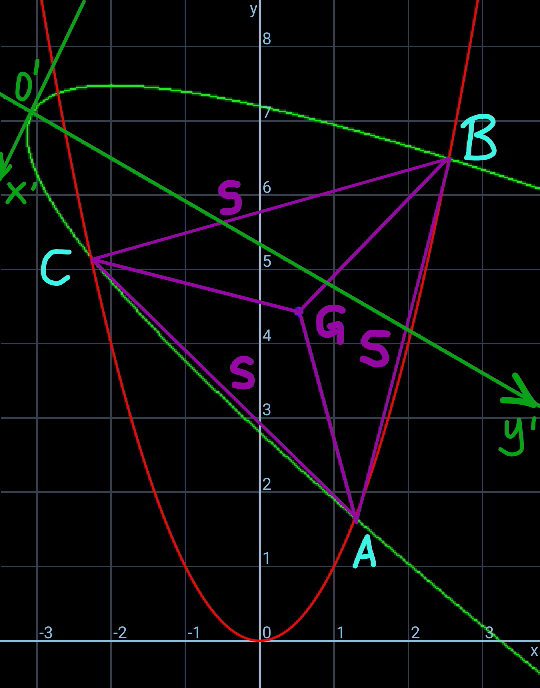
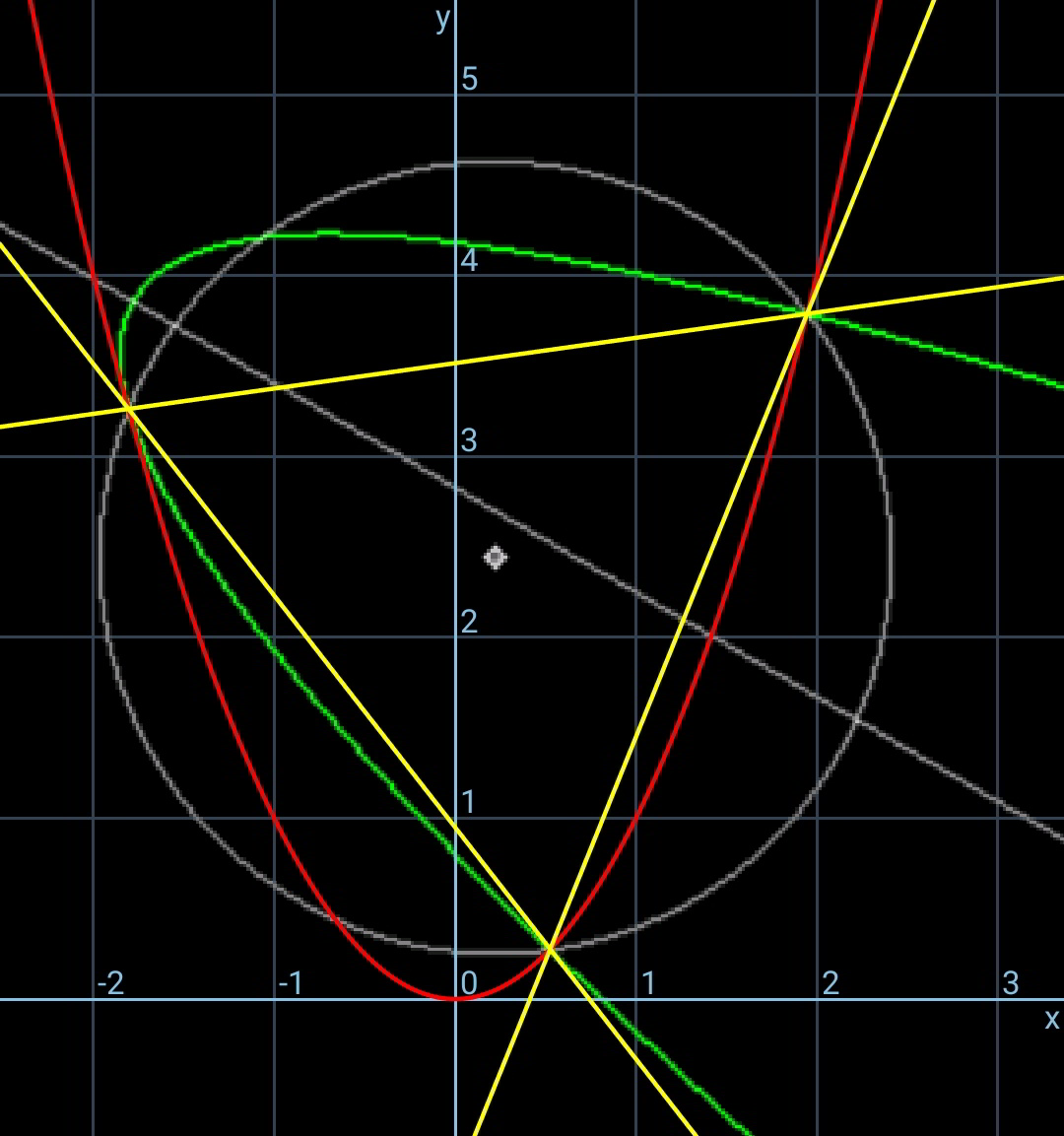
since both parabolas have the same shape and the triangle is equilateral, the correlation between the second parabola and the triangle is the same as the correlation between the first parabola and the triangle. the second parabola is just the first parabola after a rotation of 120° about the centroid G of the triangle. and the point A is rotated to the position of point C, point B to the position of point A, point C to the position of point B. from Q55613 we know: when a curve y=f(x) is rotated about the point (h,k) by an angle θ (clockwise +), it becomes the curce v=f(u) with u=(x−h) cos θ−(y−k) sin θ+h v=(x−h) sin θ+(y−k) cos θ+k in current case: θ=120° from y=x^2 we get then ((√3)/2)(x−h)−(1/2)(y−k)+k = [−(1/2)(x−h)−((√3)/2)(y−k)+h]^2 or 2(√3)(x−h)−2y+3k=[x−2h+(√3)(y−k)]^2 this is the equation of the second parabola with h=(√((s^2 /(48))−(1/4))) k=((3s^2 )/(16))−(1/4) but there is an other condition: both parabolas should touch each other at point C.
$${since}\:{both}\:{parabolas}\:{have}\:{the}\:{same} \\ $$$${shape}\:{and}\:{the}\:{triangle}\:{is}\:{equilateral}, \\ $$$${the}\:{correlation}\:{between}\:{the}\:{second} \\ $$$${parabola}\:{and}\:{the}\:{triangle}\:{is}\:{the}\:{same} \\ $$$${as}\:{the}\:{correlation}\:{between}\:{the}\:{first} \\ $$$${parabola}\:{and}\:{the}\:{triangle}.\:{the}\:{second} \\ $$$${parabola}\:{is}\:{just}\:{the}\:{first}\:{parabola} \\ $$$${after}\:{a}\:{rotation}\:{of}\:\mathrm{120}°\:{about}\:{the} \\ $$$${centroid}\:{G}\:{of}\:{the}\:{triangle}.\:{and}\:{the} \\ $$$${point}\:{A}\:{is}\:{rotated}\:{to}\:{the}\:{position} \\ $$$${of}\:{point}\:{C},\:{point}\:{B}\:{to}\:{the}\:{position}\:{of} \\ $$$${point}\:{A},\:{point}\:{C}\:{to}\:{the}\:{position}\:{of} \\ $$$${point}\:{B}. \\ $$$$ \\ $$$${from}\:{Q}\mathrm{55613}\:{we}\:{know}:\:{when}\:{a}\:{curve} \\ $$$${y}={f}\left({x}\right)\:{is}\:{rotated}\:{about}\:{the}\:{point}\:\left({h},{k}\right) \\ $$$${by}\:{an}\:{angle}\:\theta\:\left({clockwise}\:+\right),\:{it}\:{becomes} \\ $$$${the}\:{curce}\:{v}={f}\left({u}\right)\:{with} \\ $$$${u}=\left({x}−{h}\right)\:\mathrm{cos}\:\theta−\left({y}−{k}\right)\:\mathrm{sin}\:\theta+{h} \\ $$$${v}=\left({x}−{h}\right)\:\mathrm{sin}\:\theta+\left({y}−{k}\right)\:\mathrm{cos}\:\theta+{k} \\ $$$$ \\ $$$${in}\:{current}\:{case}: \\ $$$$\theta=\mathrm{120}° \\ $$$${from}\:{y}={x}^{\mathrm{2}} \:{we}\:{get}\:{then} \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left({x}−{h}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left({y}−{k}\right)+{k}\:= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[−\frac{\mathrm{1}}{\mathrm{2}}\left({x}−{h}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left({y}−{k}\right)+{h}\right]^{\mathrm{2}} \\ $$$${or} \\ $$$$\mathrm{2}\sqrt{\mathrm{3}}\left({x}−{h}\right)−\mathrm{2}{y}+\mathrm{3}{k}=\left[{x}−\mathrm{2}{h}+\sqrt{\mathrm{3}}\left({y}−{k}\right)\right]^{\mathrm{2}} \\ $$$$ \\ $$$${this}\:{is}\:{the}\:{equation}\:{of}\:{the}\:{second} \\ $$$${parabola}\:{with} \\ $$$${h}=\sqrt{\frac{{s}^{\mathrm{2}} }{\mathrm{48}}−\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$${k}=\frac{\mathrm{3}{s}^{\mathrm{2}} }{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$$${but}\:{there}\:{is}\:{an}\:{other}\:{condition}: \\ $$$${both}\:{parabolas}\:{should}\:{touch}\:{each}\:{other} \\ $$$${at}\:{point}\:{C}. \\ $$
Commented by mr W last updated on 17/Apr/20
Commented by ajfour last updated on 18/Apr/20
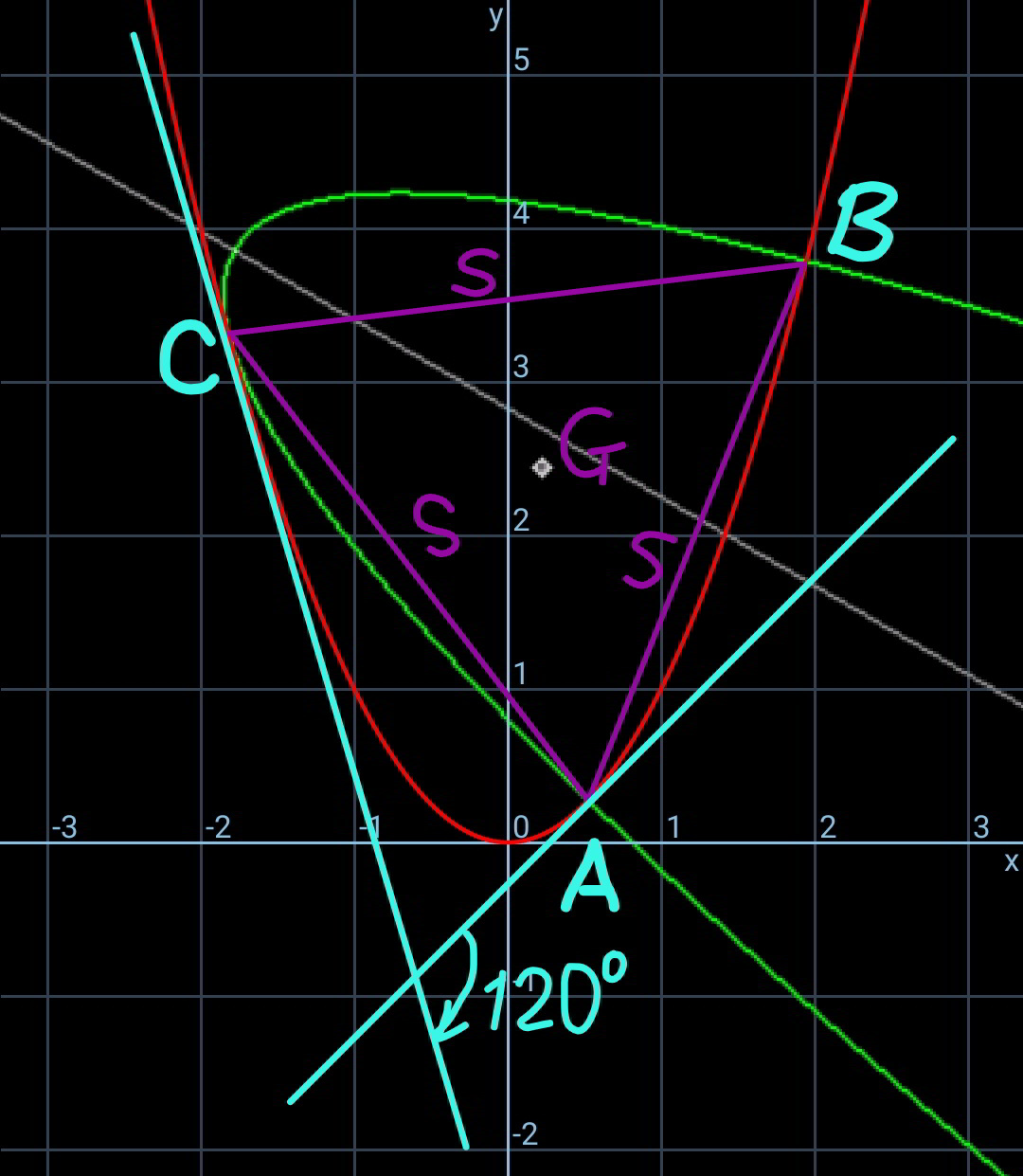
hence side of triangle, remains to be obtained.. side of triangle under the tangency condition, must be unique.
Commented by mr W last updated on 24/Apr/20
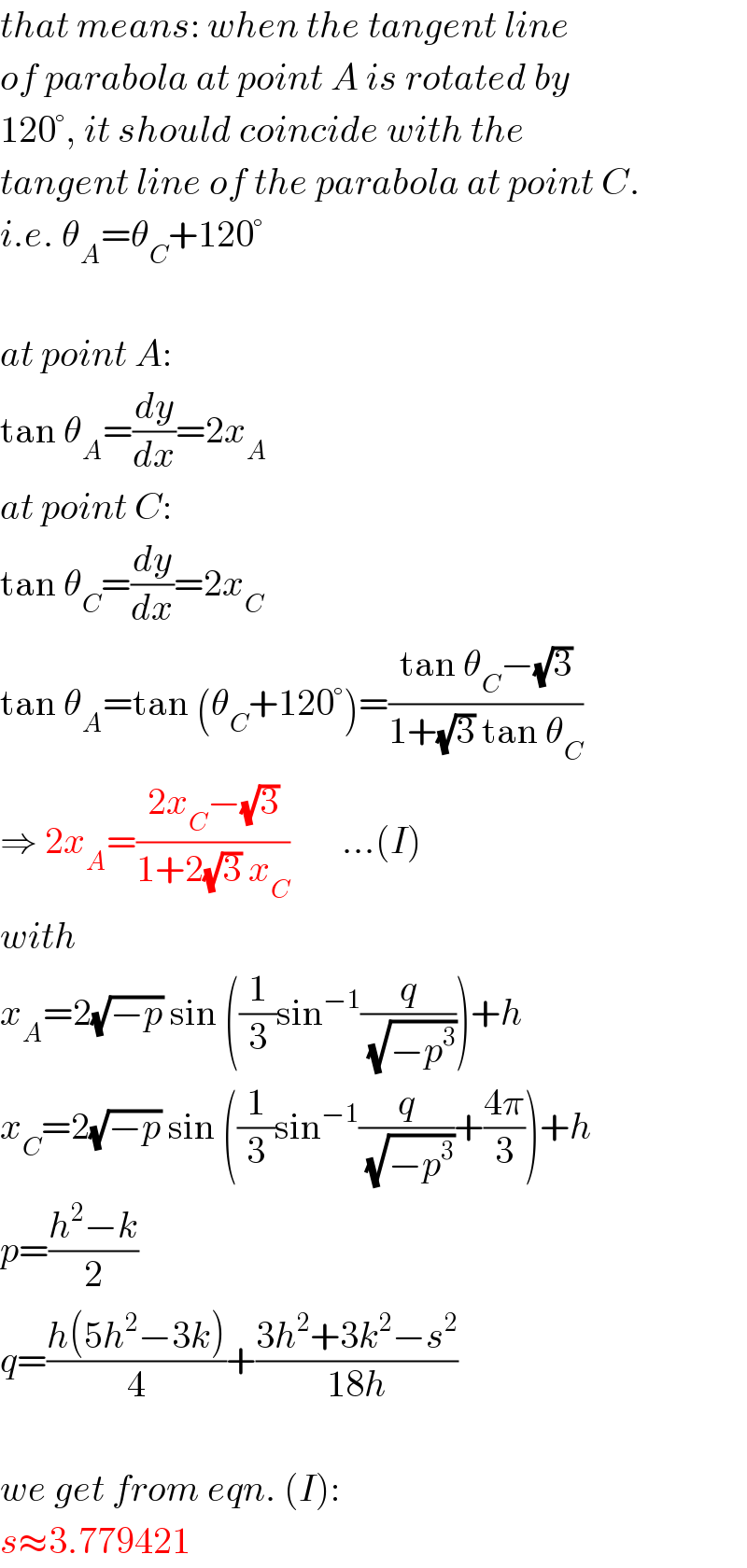
that means: when the tangent line of parabola at point A is rotated by 120°, it should coincide with the tangent line of the parabola at point C. i.e. θ_A =θ_C +120° at point A: tan θ_A =(dy/dx)=2x_A at point C: tan θ_C =(dy/dx)=2x_C tan θ_A =tan (θ_C +120°)=((tan θ_C −(√3))/(1+(√3) tan θ_C )) ⇒ 2x_A =((2x_C −(√3))/(1+2(√3) x_C )) ...(I) with x_A =2(√(−p)) sin ((1/3)sin^(−1) (q/( (√(−p^3 )))))+h x_C =2(√(−p)) sin ((1/3)sin^(−1) (q/( (√(−p^3 ))))+((4π)/3))+h p=((h^2 −k)/2) q=((h(5h^2 −3k))/4)+((3h^2 +3k^2 −s^2 )/(18h)) we get from eqn. (I): s≈3.779421
$${that}\:{means}:\:{when}\:{the}\:{tangent}\:{line} \\ $$$${of}\:{parabola}\:{at}\:{point}\:{A}\:{is}\:{rotated}\:{by} \\ $$$$\mathrm{120}°,\:{it}\:{should}\:{coincide}\:{with}\:{the} \\ $$$${tangent}\:{line}\:{of}\:{the}\:{parabola}\:{at}\:{point}\:{C}. \\ $$$${i}.{e}.\:\theta_{{A}} =\theta_{{C}} +\mathrm{120}° \\ $$$$ \\ $$$${at}\:{point}\:{A}: \\ $$$$\mathrm{tan}\:\theta_{{A}} =\frac{{dy}}{{dx}}=\mathrm{2}{x}_{{A}} \\ $$$${at}\:{point}\:{C}: \\ $$$$\mathrm{tan}\:\theta_{{C}} =\frac{{dy}}{{dx}}=\mathrm{2}{x}_{{C}} \\ $$$$\mathrm{tan}\:\theta_{{A}} =\mathrm{tan}\:\left(\theta_{{C}} +\mathrm{120}°\right)=\frac{\mathrm{tan}\:\theta_{{C}} −\sqrt{\mathrm{3}}}{\mathrm{1}+\sqrt{\mathrm{3}}\:\mathrm{tan}\:\theta_{{C}} } \\ $$$$\Rightarrow\:\mathrm{2}{x}_{{A}} =\frac{\mathrm{2}{x}_{{C}} −\sqrt{\mathrm{3}}}{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}\:{x}_{{C}} }\:\:\:\:\:\:\:…\left({I}\right) \\ $$$${with} \\ $$$${x}_{{A}} =\mathrm{2}\sqrt{−{p}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{{q}}{\:\sqrt{−{p}^{\mathrm{3}} }}\right)+{h} \\ $$$${x}_{{C}} =\mathrm{2}\sqrt{−{p}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{{q}}{\:\sqrt{−{p}^{\mathrm{3}} }}+\frac{\mathrm{4}\pi}{\mathrm{3}}\right)+{h} \\ $$$${p}=\frac{{h}^{\mathrm{2}} −{k}}{\mathrm{2}} \\ $$$${q}=\frac{{h}\left(\mathrm{5}{h}^{\mathrm{2}} −\mathrm{3}{k}\right)}{\mathrm{4}}+\frac{\mathrm{3}{h}^{\mathrm{2}} +\mathrm{3}{k}^{\mathrm{2}} −{s}^{\mathrm{2}} }{\mathrm{18}{h}} \\ $$$$ \\ $$$${we}\:{get}\:{from}\:{eqn}.\:\left({I}\right): \\ $$$${s}\approx\mathrm{3}.\mathrm{779421} \\ $$
Commented by mr W last updated on 18/Apr/20
Commented by ajfour last updated on 18/Apr/20
But afterall its you who solved it really, i was very puzzled, so thank you enormously Sir.
$${But}\:{afterall}\:{its}\:{you}\:{who}\:{solved} \\ $$$${it}\:{really},\:{i}\:{was}\:{very}\:{puzzled},\:{so} \\ $$$${thank}\:{you}\:{enormously}\:{Sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *