Question Number 89290 by I want to learn more last updated on 16/Apr/20

Commented by jagoll last updated on 16/Apr/20
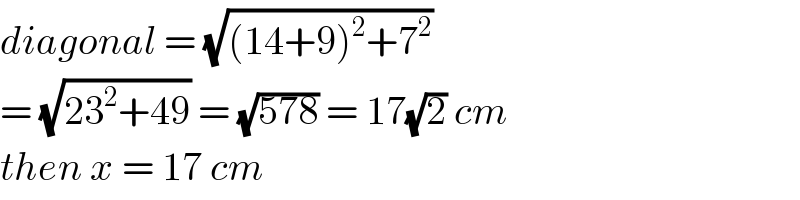
$${diagonal}\:=\:\sqrt{\left(\mathrm{14}+\mathrm{9}\right)^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} } \\ $$$$=\:\sqrt{\mathrm{23}^{\mathrm{2}} +\mathrm{49}}\:=\:\sqrt{\mathrm{578}}\:=\:\mathrm{17}\sqrt{\mathrm{2}}\:{cm} \\ $$$${then}\:{x}\:=\:\mathrm{17}\:{cm} \\ $$
Commented by I want to learn more last updated on 16/Apr/20
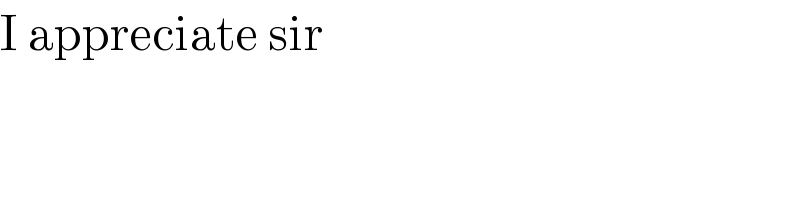
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$
Answered by TANMAY PANACEA. last updated on 16/Apr/20
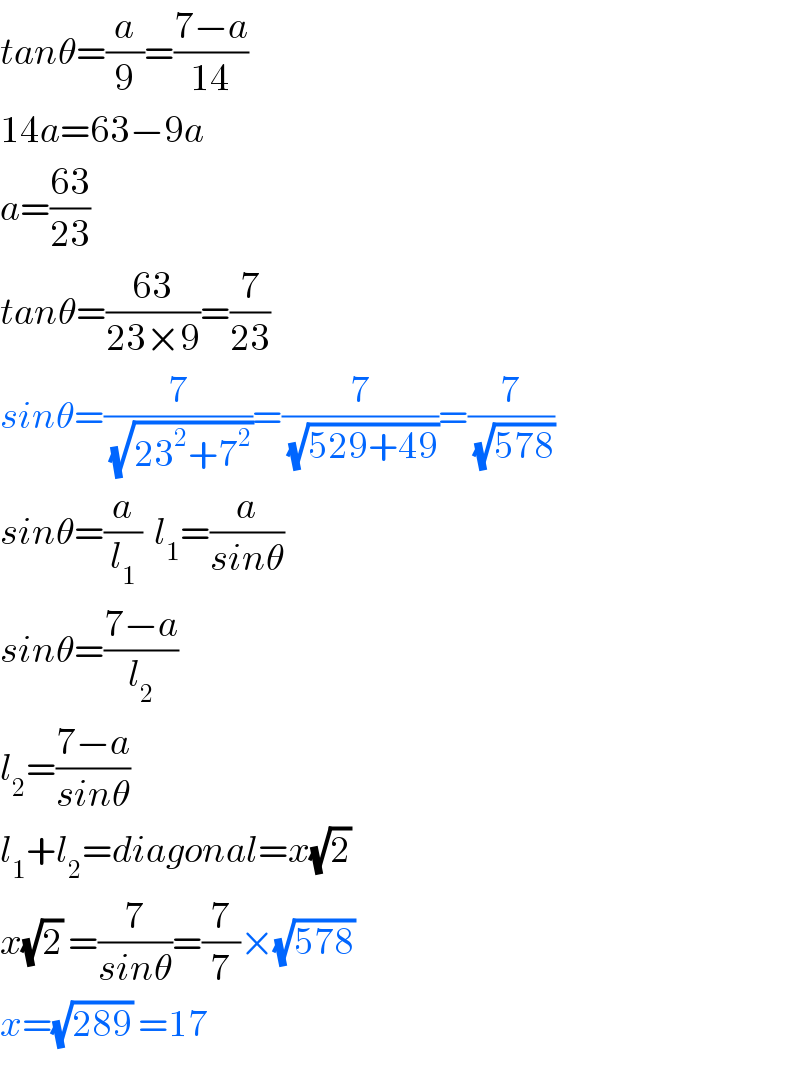
$${tan}\theta=\frac{{a}}{\mathrm{9}}=\frac{\mathrm{7}−{a}}{\mathrm{14}} \\ $$$$\mathrm{14}{a}=\mathrm{63}−\mathrm{9}{a} \\ $$$${a}=\frac{\mathrm{63}}{\mathrm{23}} \\ $$$${tan}\theta=\frac{\mathrm{63}}{\mathrm{23}×\mathrm{9}}=\frac{\mathrm{7}}{\mathrm{23}} \\ $$$${sin}\theta=\frac{\mathrm{7}}{\:\sqrt{\mathrm{23}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} }}=\frac{\mathrm{7}}{\:\sqrt{\mathrm{529}+\mathrm{49}}}=\frac{\mathrm{7}}{\:\sqrt{\mathrm{578}}} \\ $$$${sin}\theta=\frac{{a}}{{l}_{\mathrm{1}} }\:\:{l}_{\mathrm{1}} =\frac{{a}}{{sin}\theta} \\ $$$${sin}\theta=\frac{\mathrm{7}−{a}}{{l}_{\mathrm{2}} } \\ $$$${l}_{\mathrm{2}} =\frac{\mathrm{7}−{a}}{{sin}\theta} \\ $$$${l}_{\mathrm{1}} +{l}_{\mathrm{2}} ={diagonal}={x}\sqrt{\mathrm{2}}\: \\ $$$${x}\sqrt{\mathrm{2}}\:=\frac{\mathrm{7}}{{sin}\theta}=\frac{\mathrm{7}}{\mathrm{7}}×\sqrt{\mathrm{578}}\: \\ $$$${x}=\sqrt{\mathrm{289}}\:=\mathrm{17} \\ $$
Commented by I want to learn more last updated on 16/Apr/20
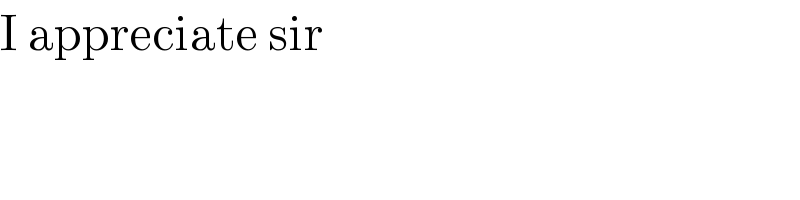
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$
