Menu Close

Question-89324

Tinku Tara 0 Comments
Pin




Question Number 89324 by 174 last updated on 16/Apr/20
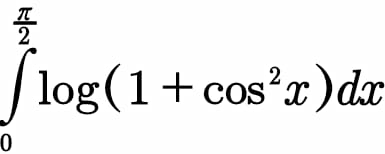
Commented by mathmax by abdo last updated on 16/Apr/20
let f(a)=∫_0 ^(π/2) ln(a+cos^2 x)dx with a>0 f^′ (a) =∫_0 ^(π/2) (dx/(a +cos^2 x))dx =∫_0 ^(π/2) (dx/(a+(1/(1+tan^2 x)))) =∫_0 ^(π/2) ((1+tan^2 x)/(a +atan^2 x +1))dx =_(tanx =t) ∫_0 ^∞ ((1+t^2 )/(at^2 +a+1)) (dt/(1+t^2 )) =∫_0 ^∞ (dt/(at^2 +a+1)) =(1/a)∫_0 ^∞ (dt/(t^2 +((a+1)/a))) =_(t =(√((a+1)/a))u) (1/a)∫_0 ^∞ (1/(((a+1)/a)(1+u^2 )))×(√((a+1)/a))du =(1/( (√a)(√(a+1))))×(π/2) =(π/(2(√a)(√(a+1)))) ⇒f(a) =(π/2)∫ (da/( (√a)(√(a+1)))) we have ∫ (da/( (√a)(√(a+1)))) =_((√a)=z) ∫ ((2zdz)/(z(√(z^2 +1)))) =2 ∫ (dz/( (√(z^2 +1)))) =2ln(z+(√(1+z^2 ))) +c =2ln((√a)+(√(1+a))) +c ⇒f(a) =πln((√a)+(√(a+1))) +C lim_(a→0^+ ) f(a) =C =2∫_0 ^(π/2) ln(cosx)dx =2(−(π/2)ln(2)) =−πln2 ⇒f(a) =πln((√a)+(√(a+1)))−πln(2) ∫_0 ^(π/2) ln(1+cos^2 x)dx =f(1) =πln(1+(√2))−πln(2) =π{ln(1+(√2))−ln(2)}
$$\:\:{let}\:\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({a}+{cos}^{\mathrm{2}} {x}\right){dx}\:\:{with}\:{a}>\mathrm{0} \\ $$$${f}^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dx}}{{a}\:+{cos}^{\mathrm{2}} {x}}{dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dx}}{{a}+\frac{\mathrm{1}}{\mathrm{1}+{tan}^{\mathrm{2}} {x}}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+{tan}^{\mathrm{2}} {x}}{{a}\:+{atan}^{\mathrm{2}} {x}\:+\mathrm{1}}{dx}\:=_{{tanx}\:={t}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}+{t}^{\mathrm{2}} }{{at}^{\mathrm{2}} \:+{a}+\mathrm{1}}\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{{dt}}{{at}^{\mathrm{2}} \:+{a}+\mathrm{1}}\:=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\frac{{a}+\mathrm{1}}{{a}}}\:=_{{t}\:=\sqrt{\frac{{a}+\mathrm{1}}{{a}}}{u}} \\ $$$$\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\frac{{a}+\mathrm{1}}{{a}}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}×\sqrt{\frac{{a}+\mathrm{1}}{{a}}}{du} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{{a}}\sqrt{{a}+\mathrm{1}}}×\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\mathrm{2}\sqrt{{a}}\sqrt{{a}+\mathrm{1}}}\:\Rightarrow{f}\left({a}\right)\:=\frac{\pi}{\mathrm{2}}\int\:\frac{{da}}{\:\sqrt{{a}}\sqrt{{a}+\mathrm{1}}} \\ $$$${we}\:{have}\:\:\int\:\:\frac{{da}}{\:\sqrt{{a}}\sqrt{{a}+\mathrm{1}}}\:=_{\sqrt{{a}}={z}} \:\:\:\:\int\:\:\frac{\mathrm{2}{zdz}}{{z}\sqrt{{z}^{\mathrm{2}} +\mathrm{1}}}\:=\mathrm{2}\:\int\:\frac{{dz}}{\:\sqrt{{z}^{\mathrm{2}} \:+\mathrm{1}}} \\ $$$$=\mathrm{2}{ln}\left({z}+\sqrt{\mathrm{1}+{z}^{\mathrm{2}} }\right)\:\:+{c}\:=\mathrm{2}{ln}\left(\sqrt{{a}}+\sqrt{\mathrm{1}+{a}}\right)\:+{c} \\ $$$$\Rightarrow{f}\left({a}\right)\:=\pi{ln}\left(\sqrt{{a}}+\sqrt{{a}+\mathrm{1}}\right)\:+{C} \\ $$$${lim}_{{a}\rightarrow\mathrm{0}^{+} } \:\:{f}\left({a}\right)\:={C}\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cosx}\right){dx}\:=\mathrm{2}\left(−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\right) \\ $$$$=−\pi{ln}\mathrm{2}\:\Rightarrow{f}\left({a}\right)\:=\pi{ln}\left(\sqrt{{a}}+\sqrt{{a}+\mathrm{1}}\right)−\pi{ln}\left(\mathrm{2}\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+{cos}^{\mathrm{2}} {x}\right){dx}\:={f}\left(\mathrm{1}\right)\:=\pi{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)−\pi{ln}\left(\mathrm{2}\right) \\ $$$$=\pi\left\{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)−{ln}\left(\mathrm{2}\right)\right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *