Question Number 89385 by pete last updated on 17/Apr/20

Commented by pete last updated on 17/Apr/20
$$\:\mathrm{I}\:\mathrm{need}\:\mathrm{help}\:\mathrm{on}\:\mathrm{the}\:\mathrm{above}\:\mathrm{question},\:\mathrm{please}. \\ $$
Answered by Joel578 last updated on 17/Apr/20

$$\mathrm{First}\:\mathrm{option} \\ $$$${PV}_{\mathrm{1}} \:=\:\mathrm{48000}{v}^{\mathrm{6}} \:+\:\mathrm{11300}{v}^{\mathrm{10}} \:=\:\$\:\mathrm{48607}.\mathrm{51} \\ $$$$ \\ $$$$\mathrm{Second}\:\mathrm{option} \\ $$$${PV}_{\mathrm{2}} \:=\:{X}\:+\:\mathrm{12100}{v}^{\mathrm{8}} \:=\:\$\:\left({X}\:+\:\mathrm{9551}.\mathrm{85}\right) \\ $$$$ \\ $$$$\mathrm{Now}, \\ $$$${PV}_{\mathrm{1}} \:=\:{PV}_{\mathrm{2}} \\ $$$$\Rightarrow\:\$\:\mathrm{48607}.\mathrm{51}\:=\:\$\:\left({X}\:+\:\mathrm{9551}.\mathrm{85}\right) \\ $$$$\Rightarrow\:{X}\:=\:\$\:\mathrm{39055}.\mathrm{65} \\ $$
Commented by Joel578 last updated on 17/Apr/20
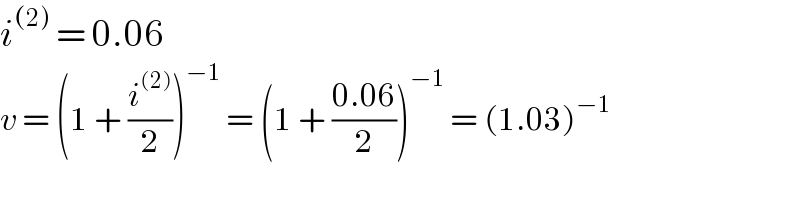
$${i}^{\left(\mathrm{2}\right)} \:=\:\mathrm{0}.\mathrm{06} \\ $$$${v}\:=\:\left(\mathrm{1}\:+\:\frac{{i}^{\left(\mathrm{2}\right)} }{\mathrm{2}}\right)^{−\mathrm{1}} \:=\:\left(\mathrm{1}\:+\:\frac{\mathrm{0}.\mathrm{06}}{\mathrm{2}}\right)^{−\mathrm{1}} \:=\:\left(\mathrm{1}.\mathrm{03}\right)^{−\mathrm{1}} \\ $$
Commented by pete last updated on 18/Apr/20

$$\mathrm{thanks}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir}\:\mathrm{Joel}. \\ $$$$\mathrm{But}\:\mathrm{please}\:\mathrm{what}\:\mathrm{does}\:\mathrm{P},\:\mathrm{V}_{\mathrm{1}} ,\:\mathrm{V}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{v}\:\mathrm{stand} \\ $$$$\mathrm{for}? \\ $$
Commented by Joel578 last updated on 19/Apr/20

$${PV}\:\mathrm{is}\:\mathrm{present}\:\mathrm{value}\:\left(\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{money}\:\mathrm{right}\:\mathrm{now}\right) \\ $$$$\mathrm{In}\:\mathrm{order}\:\mathrm{to}\:\mathrm{determine}\:\mathrm{the}\:\mathrm{upfront}\:\mathrm{amnout}\:{now}, \\ $$$$\mathrm{we}\:\mathrm{should}\:\mathrm{know}\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\$\:\mathrm{48000}\:\mathrm{and}\: \\ $$$$\$\:\mathrm{11300}\:\mathrm{if}\:\mathrm{they}\:\mathrm{are}\:\mathrm{given}\:{right}\:{now}. \\ $$$$ \\ $$$${v}\:\mathrm{is}\:\mathrm{discount}\:\mathrm{factor}\:=\:\left(\mathrm{1}\:+\:{i}\right)^{−\mathrm{1}} \\ $$$$\mathrm{Let}'\mathrm{s}\:\mathrm{say}\:\mathrm{you}\:\mathrm{deposits}\:\${K}\:\mathrm{on}\:\mathrm{a}\:\mathrm{bank},\:\mathrm{which}\:\mathrm{give}\:\mathrm{you} \\ $$$$\mathrm{effective}\:\mathrm{annual}\:\mathrm{interest}\:\mathrm{rate}\:{i}.\:\mathrm{Then},\:\mathrm{after}\:{n}\:\mathrm{years}\:\mathrm{from}\:{now}, \\ $$$$\mathrm{your}\:\mathrm{deposit}\:\mathrm{is}\:\${K}\left(\mathrm{1}+{i}\right)^{{n}} \:\rightarrow\:{Future}\:{Value}\:\left({FV}\right) \\ $$$$ \\ $$$$\mathrm{If}\:\mathrm{you}\:\mathrm{know}\:\mathrm{the}\:\mathrm{Future}\:\mathrm{Value},\:\mathrm{then}\:\mathrm{you}\:\mathrm{can}\:\mathrm{find} \\ $$$$\mathrm{its}\:\mathrm{Present}\:\mathrm{Value}\:\left(=\:\${K}\right) \\ $$$$\mathrm{P}{V}\:=\:{FV}\:\:{v}^{{n}} \:=\:\${K}\left(\mathrm{1}+{i}\right)^{{n}} \:.\:\left(\mathrm{1}+{i}\right)^{−{n}} \:=\:\${K} \\ $$
Commented by pete last updated on 25/Apr/20
$$\mathrm{may}\:\mathrm{you}\:\mathrm{continually}\:\mathrm{increase}\:\mathrm{in}\:\mathrm{knowledge} \\ $$$$\mathrm{as}\:\mathrm{you}\:\mathrm{continue}\:\mathrm{to}\:\mathrm{give}\:\mathrm{help},\:\mathrm{Sir} \\ $$
