Question Number 89412 by I want to learn more last updated on 17/Apr/20

Commented by I want to learn more last updated on 17/Apr/20
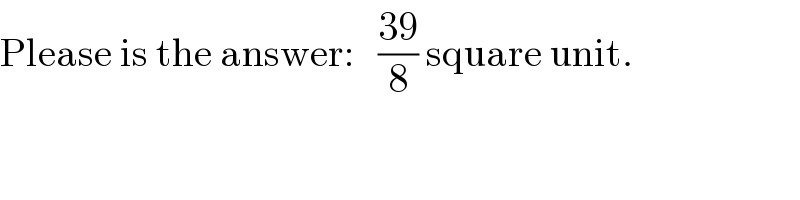
$$\mathrm{Please}\:\mathrm{is}\:\mathrm{the}\:\mathrm{answer}:\:\:\:\frac{\mathrm{39}}{\mathrm{8}}\:\mathrm{square}\:\mathrm{unit}. \\ $$
Commented by jagoll last updated on 17/Apr/20
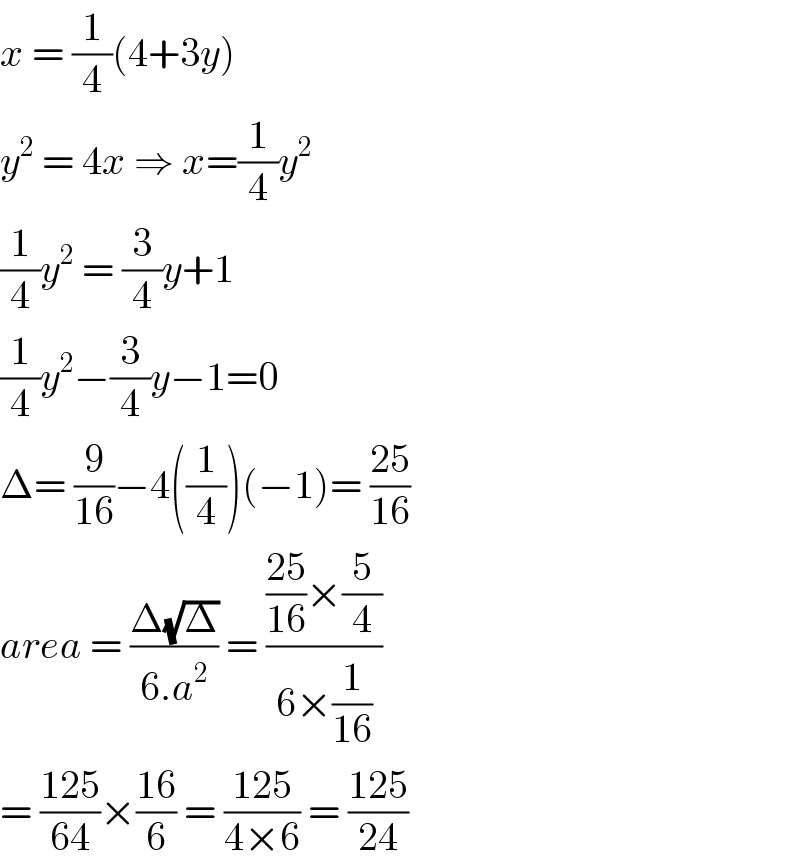
$${x}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{4}+\mathrm{3}{y}\right)\: \\ $$$${y}^{\mathrm{2}} \:=\:\mathrm{4}{x}\:\Rightarrow\:{x}=\frac{\mathrm{1}}{\mathrm{4}}{y}^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{y}^{\mathrm{2}} \:=\:\frac{\mathrm{3}}{\mathrm{4}}{y}+\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{y}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}{y}−\mathrm{1}=\mathrm{0} \\ $$$$\Delta=\:\frac{\mathrm{9}}{\mathrm{16}}−\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\left(−\mathrm{1}\right)=\:\frac{\mathrm{25}}{\mathrm{16}} \\ $$$${area}\:=\:\frac{\Delta\sqrt{\Delta}}{\mathrm{6}.{a}^{\mathrm{2}} }\:=\:\frac{\frac{\mathrm{25}}{\mathrm{16}}×\frac{\mathrm{5}}{\mathrm{4}}}{\mathrm{6}×\frac{\mathrm{1}}{\mathrm{16}}} \\ $$$$=\:\frac{\mathrm{125}}{\mathrm{64}}×\frac{\mathrm{16}}{\mathrm{6}}\:=\:\frac{\mathrm{125}}{\mathrm{4}×\mathrm{6}}\:=\:\frac{\mathrm{125}}{\mathrm{24}} \\ $$
Commented by jagoll last updated on 17/Apr/20
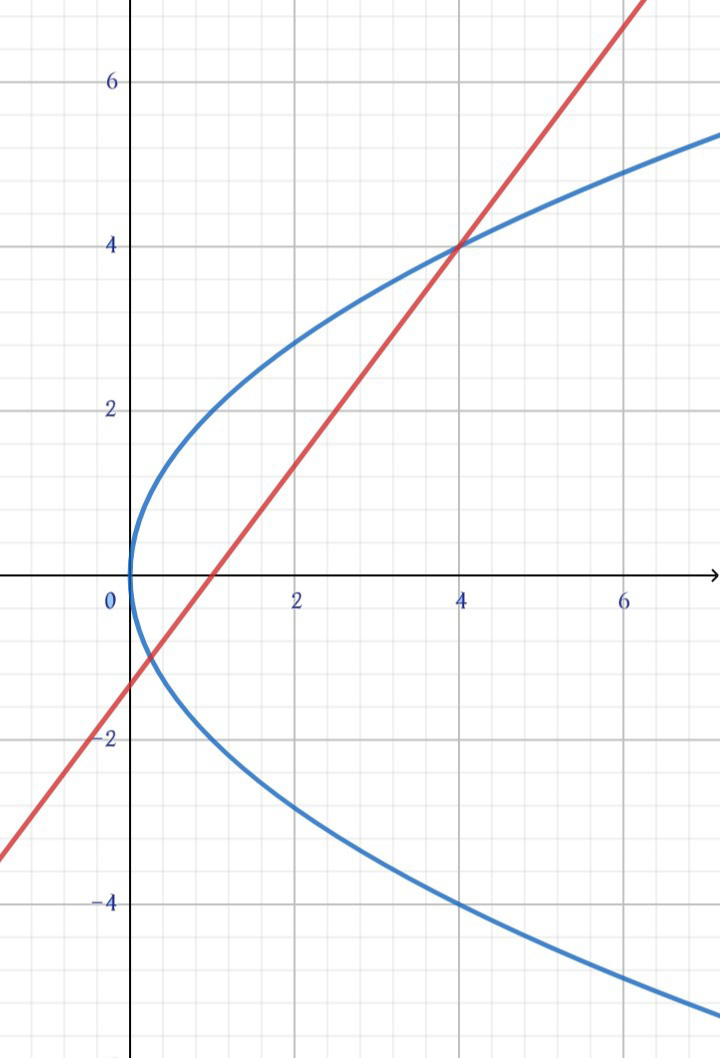
Commented by I want to learn more last updated on 17/Apr/20
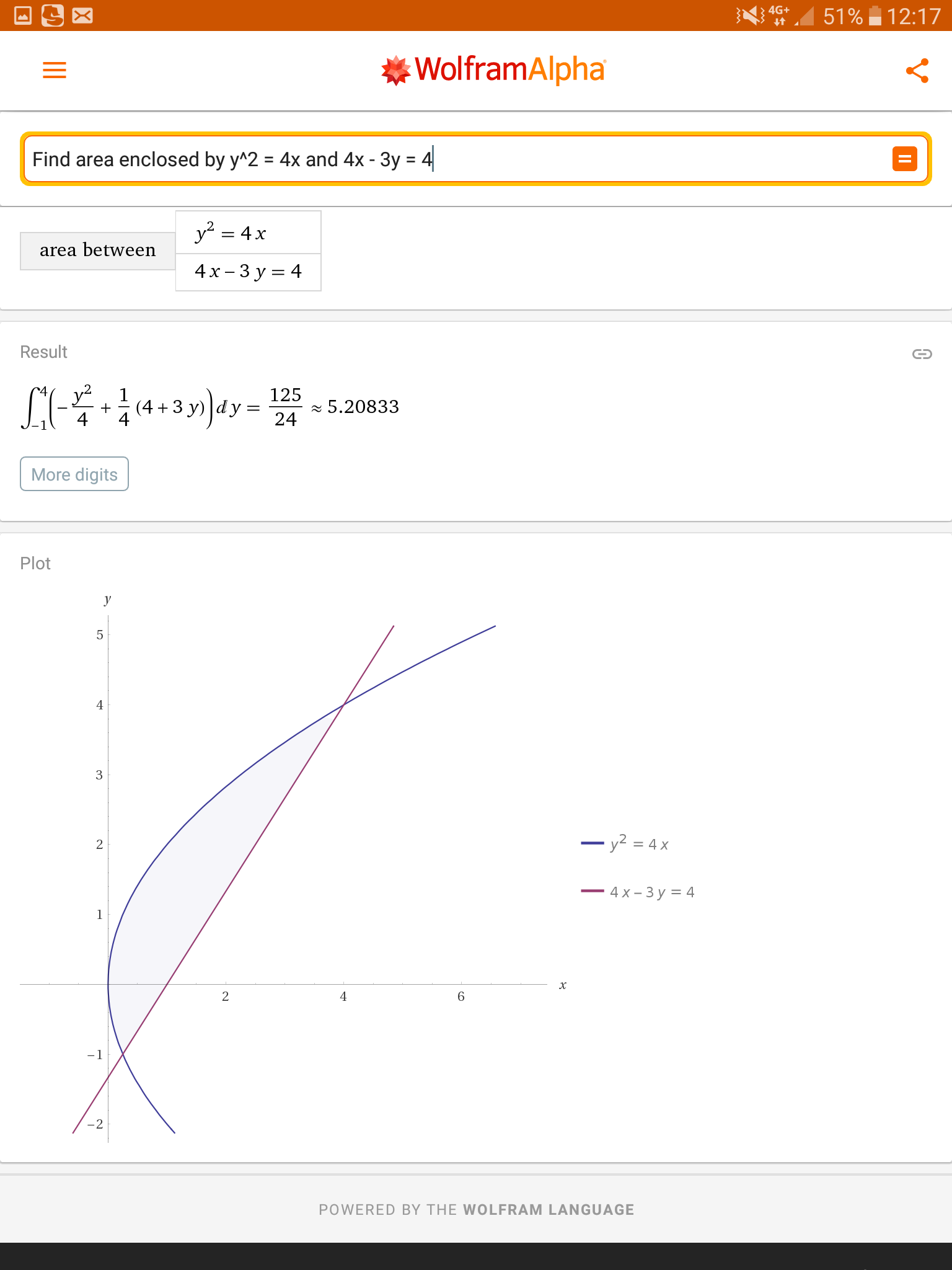
Commented by I want to learn more last updated on 17/Apr/20

$$\mathrm{Sir},\:\mathrm{wolfram}\:\mathrm{says}\:\:\:\:\frac{\mathrm{125}}{\mathrm{24}},\:\:\:\mathrm{where}\:\mathrm{is}\:\mathrm{the}\:\mathrm{error}\:\mathrm{sir}\:\mathrm{or}\:\mathrm{wolfram}\:\mathrm{wrong}.\:\mathrm{Thanks} \\ $$
Commented by I want to learn more last updated on 17/Apr/20
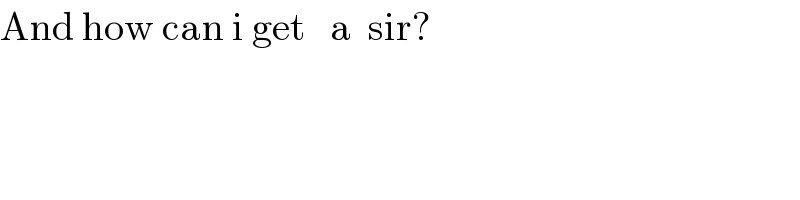
$$\mathrm{And}\:\mathrm{how}\:\mathrm{can}\:\mathrm{i}\:\mathrm{get}\:\:\:\mathrm{a}\:\:\mathrm{sir}? \\ $$
Commented by jagoll last updated on 17/Apr/20
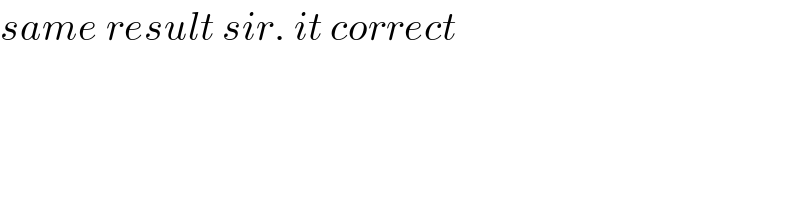
$${same}\:{result}\:{sir}.\:{it}\:{correct} \\ $$
Commented by I want to learn more last updated on 17/Apr/20

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
