Menu Close

Question-89422

Tinku Tara 0 Comments
Pin




Question Number 89422 by naka3546 last updated on 17/Apr/20
Commented by jagoll last updated on 17/Apr/20
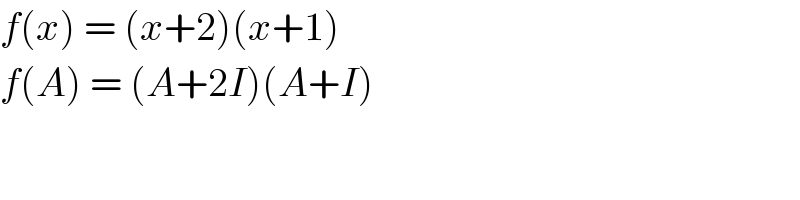
f(x) = (x+2)(x+1) f(A) = (A+2I)(A+I)
f(x)=(x+2)(x+1)f(A)=(A+2I)(A+I)
Answered by som(math1967) last updated on 17/Apr/20
f(A)=A^2 +3A+2I = [(1,(−2)),(2,(−1)) ] [(1,(−2)),(2,(−1)) ]+3 [(1,(−2)),(2,(−1)) ] +2 [(1,0),(0,1) ] = [((−3),0),(0,(−3)) ]+ [(3,(−6)),(6,(−3)) ]+ [(2,0),(0,2) ] = [((−3+3+2),(0−6+0)),((0+6+0),(−3−3+2)) ] = determinant ((2,(−6)),(6,(−4)))....ansB
f(A)=A2+3A+2I=[1−22−1][1−22−1]+3[1−22−1]+2[1001]=[−300−3]+[3−66−3]+[2002]=[−3+3+20−6+00+6+0−3−3+2]=|2−66−4|….ansB
Commented by naka3546 last updated on 17/Apr/20
thank you
thankyou

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *