Question Number 89534 by mathocean1 last updated on 17/Apr/20

Commented by abdomathmax last updated on 17/Apr/20
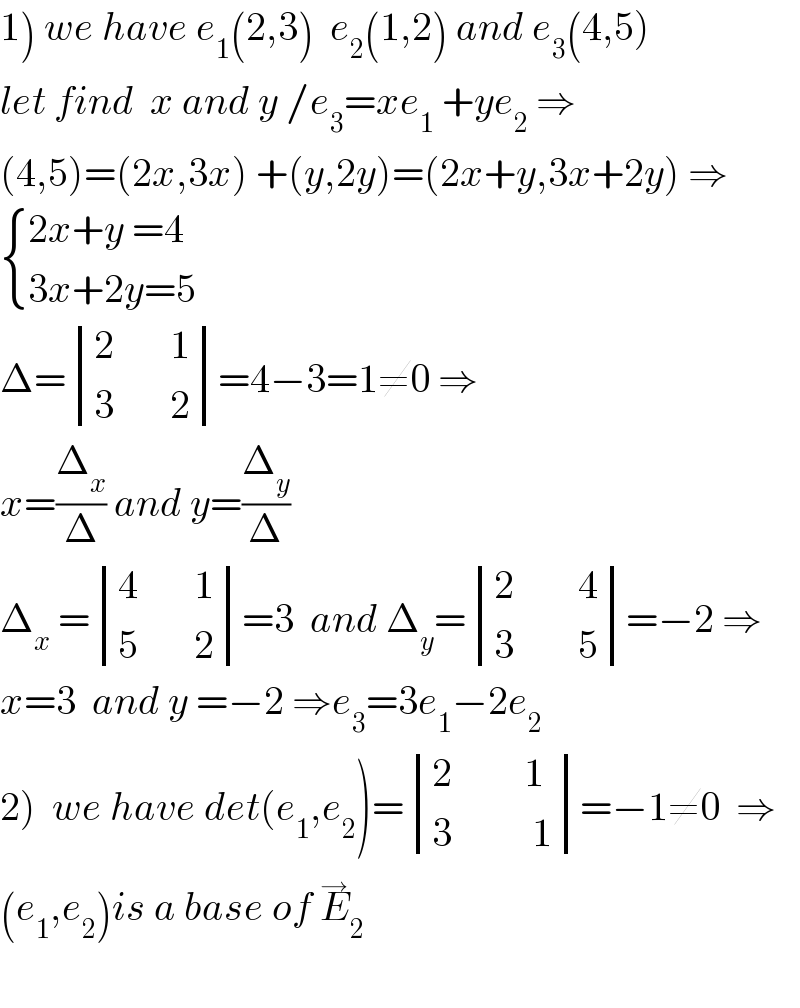
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{e}_{\mathrm{1}} \left(\mathrm{2},\mathrm{3}\right)\:\:{e}_{\mathrm{2}} \left(\mathrm{1},\mathrm{2}\right)\:{and}\:{e}_{\mathrm{3}} \left(\mathrm{4},\mathrm{5}\right) \\ $$$${let}\:{find}\:\:{x}\:{and}\:{y}\:/{e}_{\mathrm{3}} ={xe}_{\mathrm{1}} \:+{ye}_{\mathrm{2}} \:\Rightarrow \\ $$$$\left(\mathrm{4},\mathrm{5}\right)=\left(\mathrm{2}{x},\mathrm{3}{x}\right)\:+\left({y},\mathrm{2}{y}\right)=\left(\mathrm{2}{x}+{y},\mathrm{3}{x}+\mathrm{2}{y}\right)\:\Rightarrow \\ $$$$\begin{cases}{\mathrm{2}{x}+{y}\:=\mathrm{4}}\\{\mathrm{3}{x}+\mathrm{2}{y}=\mathrm{5}}\end{cases} \\ $$$$\Delta=\begin{vmatrix}{\mathrm{2}\:\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{3}\:\:\:\:\:\:\:\mathrm{2}}\end{vmatrix}=\mathrm{4}−\mathrm{3}=\mathrm{1}\neq\mathrm{0}\:\Rightarrow \\ $$$${x}=\frac{\Delta_{{x}} }{\Delta}\:{and}\:{y}=\frac{\Delta_{{y}} }{\Delta} \\ $$$$\Delta_{{x}} \:=\begin{vmatrix}{\mathrm{4}\:\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{5}\:\:\:\:\:\:\:\mathrm{2}}\end{vmatrix}=\mathrm{3}\:\:{and}\:\Delta_{{y}} =\begin{vmatrix}{\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{4}}\\{\mathrm{3}\:\:\:\:\:\:\:\:\mathrm{5}}\end{vmatrix}=−\mathrm{2}\:\Rightarrow \\ $$$${x}=\mathrm{3}\:\:{and}\:{y}\:=−\mathrm{2}\:\Rightarrow{e}_{\mathrm{3}} =\mathrm{3}{e}_{\mathrm{1}} −\mathrm{2}{e}_{\mathrm{2}} \\ $$$$\left.\mathrm{2}\right)\:\:{we}\:{have}\:{det}\left({e}_{\mathrm{1}} ,{e}_{\mathrm{2}} \right)=\begin{vmatrix}{\mathrm{2}\:\:\:\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{3}\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{vmatrix}=−\mathrm{1}\neq\mathrm{0}\:\:\Rightarrow \\ $$$$\left({e}_{\mathrm{1}} ,{e}_{\mathrm{2}} \right){is}\:{a}\:{base}\:{of}\:\overset{\rightarrow} {{E}}_{\mathrm{2}} \\ $$$$ \\ $$
Commented by mathocean1 last updated on 18/Apr/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}! \\ $$
