Question Number 89618 by ajfour last updated on 18/Apr/20
Commented by ajfour last updated on 18/Apr/20
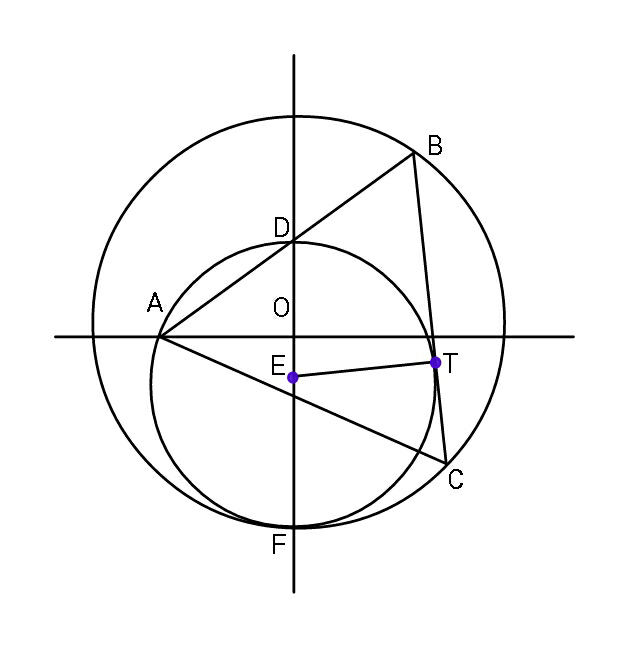
$${Find}\:{radii}\:{of}\:{the}\:{circles},\:{if} \\ $$$$\bigtriangleup{ABC}\:{is}\:{equilateral}\:{of}\:{side}\:{a}. \\ $$$$\left({E}\:{is}\:{the}\:{center}\:{of}\:{smaller}\:{circle}\right) \\ $$
Commented by ajfour last updated on 19/Apr/20
$${Any}\:{smooth}\:{way}\:{for}\:{this}\:{Q}. \\ $$$${Sir}\:? \\ $$
Answered by ajfour last updated on 18/Apr/20

$${eq}.\:{AB}:\:\:\:{y}_{{B}} =\frac{\left(\mathrm{2}{r}−{R}\right){x}_{{B}} }{\:\sqrt{{r}^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} }}+\mathrm{2}{r}−{R} \\ $$$${x}_{{B}} ^{\mathrm{2}} +\left(\mathrm{2}{r}−{R}\right)^{\mathrm{2}} \left(\mathrm{1}+\frac{{x}_{{B}} }{\:\sqrt{{r}\left(\mathrm{2}{R}−{r}\right)}}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\left({x}_{{B}} +\sqrt{{r}\left(\mathrm{2}{R}−{r}\right)}\right)^{\mathrm{2}} +{y}_{{B}} ^{\mathrm{2}} ={a}^{\mathrm{2}} =\mathrm{1}\:\left({say}\right) \\ $$$${eq}.\:{of}\:{BC}: \\ $$$${y}−{y}_{{B}} =\frac{{m}+\sqrt{\mathrm{3}}}{\mathrm{1}−{m}\sqrt{\mathrm{3}}}\left({x}−{x}_{{B}} \right) \\ $$$${m}=\frac{\mathrm{2}{r}−{R}}{\:\sqrt{{r}\left(\mathrm{2}{R}−{r}\right)}}\:\:\:\:\:….\left({i}\right) \\ $$$$\frac{\mid{y}_{{B}} +{R}−{r}−\left(\frac{{m}+\sqrt{\mathrm{3}}}{\mathrm{1}−{m}\sqrt{\mathrm{3}}}\right){x}_{{B}} \mid}{\:\sqrt[{}]{\mathrm{1}+\left(\frac{{m}+\sqrt{\mathrm{3}}}{\mathrm{1}−{m}\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }}={r}\:\:\:…\left({ii}\right) \\ $$$$\frac{\mid{y}_{{B}} −\left(\frac{{m}+\sqrt{\mathrm{3}}}{\mathrm{1}−{m}\sqrt{\mathrm{3}}}\right)\left(\sqrt{{r}\left(\mathrm{2}{R}−{r}\right)}+{x}_{{B}} \right)\mid}{\:\sqrt[{}]{\mathrm{1}+\left(\frac{{m}+\sqrt{\mathrm{3}}}{\mathrm{1}−{m}\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…….\left({iii}\right) \\ $$$$….. \\ $$
