Question-89653

Question Number 89653 by student work last updated on 18/Apr/20

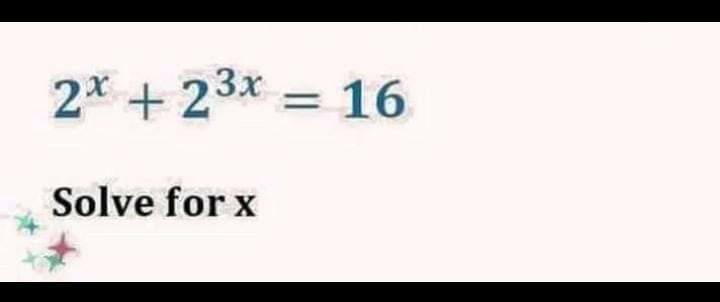
Commented by john santu last updated on 18/Apr/20

2^x = p ⇒ p^3 + p = 16 use Cardano method

$$\mathrm{2}^{{x}} \:=\:{p}\:\Rightarrow\:{p}^{\mathrm{3}} \:+\:{p}\:=\:\mathrm{16}\: \\ $$$${use}\:{Cardano}\:{method}\: \\ $$

Commented by student work last updated on 18/Apr/20

$${solve}\:{for}\:{me} \\ $$

Commented by student work last updated on 18/Apr/20

$${can}\:{u}\:{descibe}\:{for}\:{me}\:{the}\:{cardano}\:{methood}? \\ $$

Commented by MJS last updated on 18/Apr/20

you can search on google if you don′t know how to solve polynomes of 3^(rd) degree you will have to study for a while

$$\mathrm{you}\:\mathrm{can}\:\mathrm{search}\:\mathrm{on}\:\mathrm{google} \\ $$$$\mathrm{if}\:\mathrm{you}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{polynomes} \\ $$$$\mathrm{of}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{degree}\:\mathrm{you}\:\mathrm{will}\:\mathrm{have}\:\mathrm{to}\:\mathrm{study}\:\mathrm{for}\:\mathrm{a}\:\mathrm{while} \\ $$

Answered by MJS last updated on 18/Apr/20

2^(3x) +2^x −16=0 z=2^x ⇔ x=((ln z)/(ln 2)) z^3 +z−16=0 ⇒ p=1∧q=−16 D=(p^3 /(27))+(q^2 /4)=((1729)/(27))>0 ⇒ Cardano′s Method z_1 =((8+((√(5187))/9)))^(1/3) −((−8+((√(5187))/9)))^(1/3) z_2 ∧z_3 ∉R ⇒ x=((ln (((8+((√(5187))/9)))^(1/3) −((−8+((√(5187))/9)))^(1/3) ))/(ln 2))

$$\mathrm{2}^{\mathrm{3}{x}} +\mathrm{2}^{{x}} −\mathrm{16}=\mathrm{0} \\ $$$${z}=\mathrm{2}^{{x}} \:\Leftrightarrow\:{x}=\frac{\mathrm{ln}\:{z}}{\mathrm{ln}\:\mathrm{2}} \\ $$$${z}^{\mathrm{3}} +{z}−\mathrm{16}=\mathrm{0}\:\Rightarrow\:{p}=\mathrm{1}\wedge{q}=−\mathrm{16} \\ $$$${D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}=\frac{\mathrm{1729}}{\mathrm{27}}>\mathrm{0}\:\Rightarrow\:\mathrm{Cardano}'\mathrm{s}\:\mathrm{Method} \\ $$$${z}_{\mathrm{1}} =\sqrt[{\mathrm{3}}]{\mathrm{8}+\frac{\sqrt{\mathrm{5187}}}{\mathrm{9}}}−\sqrt[{\mathrm{3}}]{−\mathrm{8}+\frac{\sqrt{\mathrm{5187}}}{\mathrm{9}}} \\ $$$${z}_{\mathrm{2}} \wedge{z}_{\mathrm{3}} \notin\mathbb{R} \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{ln}\:\left(\sqrt[{\mathrm{3}}]{\mathrm{8}+\frac{\sqrt{\mathrm{5187}}}{\mathrm{9}}}−\sqrt[{\mathrm{3}}]{−\mathrm{8}+\frac{\sqrt{\mathrm{5187}}}{\mathrm{9}}}\right)}{\mathrm{ln}\:\mathrm{2}} \\ $$

Commented by mr W last updated on 18/Apr/20

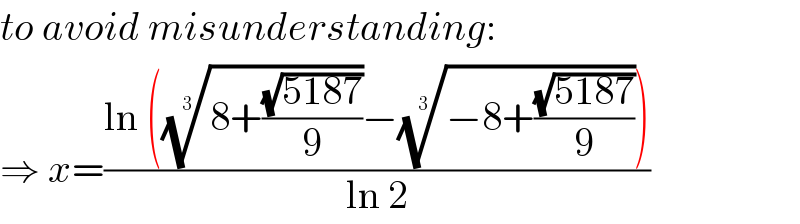
to avoid misunderstanding: ⇒ x=((ln (((8+((√(5187))/9)))^(1/3) −((−8+((√(5187))/9)))^(1/3) ))/(ln 2))

$${to}\:{avoid}\:{misunderstanding}: \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{ln}\:\left(\sqrt[{\mathrm{3}}]{\mathrm{8}+\frac{\sqrt{\mathrm{5187}}}{\mathrm{9}}}−\sqrt[{\mathrm{3}}]{−\mathrm{8}+\frac{\sqrt{\mathrm{5187}}}{\mathrm{9}}}\right)}{\mathrm{ln}\:\mathrm{2}} \\ $$

Commented by MJS last updated on 18/Apr/20

thank you... btw: is it a typo to not type?

$$\mathrm{thank}\:\mathrm{you}… \\ $$$$\mathrm{btw}:\:\mathrm{is}\:\mathrm{it}\:\mathrm{a}\:\mathrm{typo}\:\mathrm{to}\:\mathrm{not}\:\mathrm{type}? \\ $$

Commented by I want to learn more last updated on 18/Apr/20

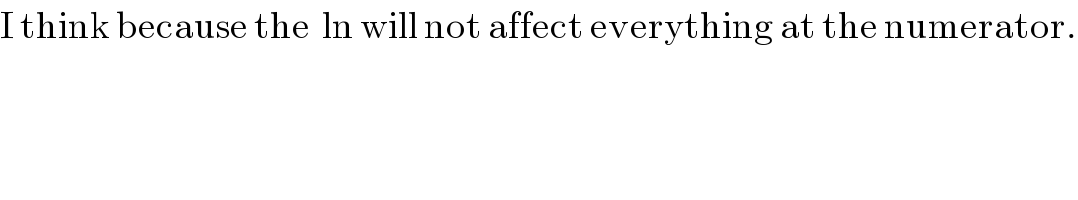
I think because the ln will not affect everything at the numerator.

$$\mathrm{I}\:\mathrm{think}\:\mathrm{because}\:\mathrm{the}\:\:\mathrm{ln}\:\mathrm{will}\:\mathrm{not}\:\mathrm{affect}\:\mathrm{everything}\:\mathrm{at}\:\mathrm{the}\:\mathrm{numerator}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply