Question Number 89781 by mr W last updated on 19/Apr/20
Commented by jagoll last updated on 19/Apr/20

$$\mathrm{A}=\:\frac{\Delta\sqrt{\Delta}}{\mathrm{6}.\mathrm{a}^{\mathrm{2}} } \\ $$
Commented by mr W last updated on 29/Apr/20
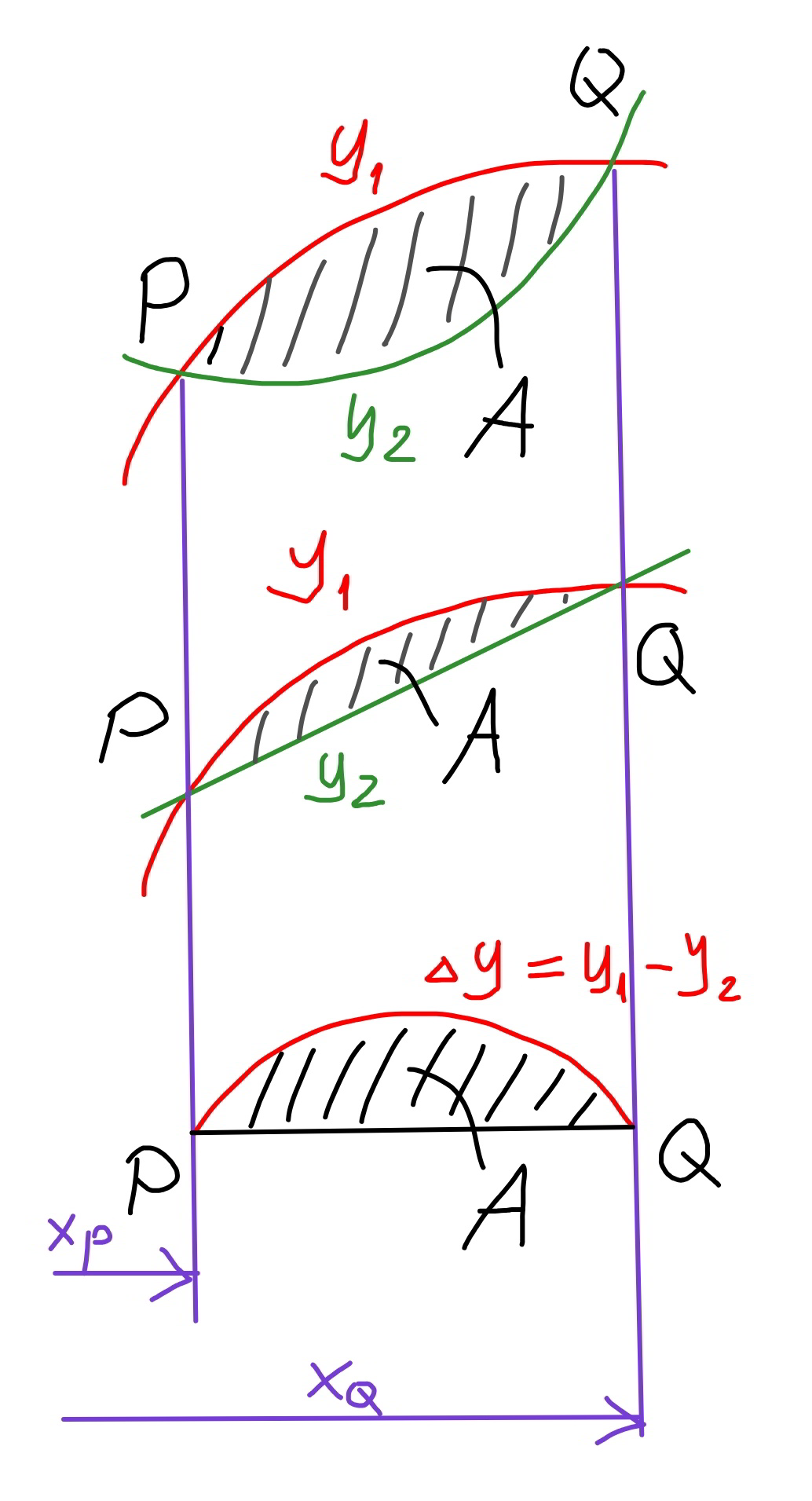
![how to quickly calculate the area bounded by two parabolas or by a parabola and a straight line recently a lot of such questions are asked. the general way to solve such questions is to apply intergral calculus. but in case of parabola, we can find some short cuts. see also Q88758. since a straight line is also a special parabola, we will only look at the case with two parabolas. parabola 1: y_1 =a_1 x^2 +b_1 x+c_1 parabola 2: y_2 =a_2 x^2 +b_2 x+c_2 Δy=y_1 −y_2 =(a_1 −a_2 )x^2 +(b_1 −b_2 )x+(c_1 −c_2 ) or Δy=ax^2 +bx+c with a=a_1 −a_2 , b=b_1 −b_2 , c=c_1 −c_2 we see Δy represents also a parabola. the area between both parabolas is: (we use ∣ ∣ since the integral can also be negative, only its absolute value is the area) A=∣∫_x_P ^x_Q (y_1 −y_2 )dx∣ A=∣∫_x_P ^x_Q (Δy)dx∣ A=∣∫_x_P ^x_Q (ax^2 +bx+c)dx∣ A=∣(a/3)(x_Q ^3 −x_P ^3 )+(b/2)(x_Q ^2 −x_P ^2 )+c(x_Q −x_P )∣ A=∣{(a/3)(x_Q ^2 +x_P x_Q +x_P ^2 )+(b/2)(x_Q +x_P )+c}(x_Q −x_P )∣ A=∣{(a/3)[(x_P +x_Q )^2 −x_P x_Q ]+(b/2)(x_Q +x_P )+c}(x_Q −x_P )∣ since x_P and x_Q are the roots of eqn. ax^2 +bx+c=0 we have D=b^2 −4ac (usually we use Δ instead of D, here i use D because i have used Δ above) x_P +x_Q =−(b/a) x_P x_Q =(c/a) x_Q −x_P =(√((x_Q +x_P )^2 −4x_P x_Q ))=(√((b^2 /a^2 )−((4c)/a)))=((√(b^2 −4ac))/a)=((√δ)/a) A=∣{(a/3)[(−(b/a))^2 −(c/a)]+(b/2)(−(b/a))+c}((√D)/a)∣ A=∣(−b^2 +4ac)((√D)/(6a^2 ))∣ A=(b^2 −4ac)((√D)/(6a^2 )) ⇒A=((D(√D))/(6a^2 )) with D=b^2 −4ac](https://www.tinkutara.com/question/Q89784.png)
$${how}\:{to}\:{quickly}\:{calculate}\:{the}\:{area}\: \\ $$$${bounded}\:{by}\:{two}\:{parabolas}\:{or}\:{by}\:{a} \\ $$$${parabola}\:{and}\:{a}\:{straight}\:{line} \\ $$$$ \\ $$$${recently}\:{a}\:{lot}\:{of}\:{such}\:{questions}\:{are} \\ $$$${asked}. \\ $$$${the}\:{general}\:{way}\:{to}\:{solve}\:{such}\:{questions} \\ $$$${is}\:{to}\:{apply}\:{intergral}\:{calculus}.\:{but}\:{in} \\ $$$${case}\:{of}\:{parabola},\:{we}\:{can}\:{find}\:{some} \\ $$$${short}\:{cuts}.\:{see}\:{also}\:{Q}\mathrm{88758}. \\ $$$$ \\ $$$${since}\:{a}\:{straight}\:{line}\:{is}\:{also}\:{a}\:{special} \\ $$$${parabola},\:{we}\:{will}\:{only}\:{look}\:{at}\:{the}\:{case} \\ $$$${with}\:{two}\:{parabolas}. \\ $$$$ \\ $$$${parabola}\:\mathrm{1}:\:{y}_{\mathrm{1}} ={a}_{\mathrm{1}} {x}^{\mathrm{2}} +{b}_{\mathrm{1}} {x}+{c}_{\mathrm{1}} \\ $$$${parabola}\:\mathrm{2}:\:{y}_{\mathrm{2}} ={a}_{\mathrm{2}} {x}^{\mathrm{2}} +{b}_{\mathrm{2}} {x}+{c}_{\mathrm{2}} \\ $$$$\Delta{y}={y}_{\mathrm{1}} −{y}_{\mathrm{2}} =\left({a}_{\mathrm{1}} −{a}_{\mathrm{2}} \right){x}^{\mathrm{2}} +\left({b}_{\mathrm{1}} −{b}_{\mathrm{2}} \right){x}+\left({c}_{\mathrm{1}} −{c}_{\mathrm{2}} \right) \\ $$$${or} \\ $$$$\Delta{y}={ax}^{\mathrm{2}} +{bx}+{c}\: \\ $$$${with}\:{a}={a}_{\mathrm{1}} −{a}_{\mathrm{2}} ,\:{b}={b}_{\mathrm{1}} −{b}_{\mathrm{2}} ,\:{c}={c}_{\mathrm{1}} −{c}_{\mathrm{2}} \\ $$$${we}\:{see}\:\Delta{y}\:{represents}\:{also}\:{a}\:{parabola}. \\ $$$$ \\ $$$${the}\:{area}\:{between}\:{both}\:{parabolas}\:{is}: \\ $$$$\left({we}\:{use}\:\mid\:\mid\:{since}\:{the}\:{integral}\:{can}\:{also}\right. \\ $$$${be}\:{negative},\:{only}\:{its}\:{absolute}\:{value}\:{is} \\ $$$$\left.{the}\:{area}\right) \\ $$$${A}=\mid\int_{{x}_{{P}} } ^{{x}_{{Q}} } \left({y}_{\mathrm{1}} −{y}_{\mathrm{2}} \right){dx}\mid \\ $$$${A}=\mid\int_{{x}_{{P}} } ^{{x}_{{Q}} } \left(\Delta{y}\right){dx}\mid \\ $$$${A}=\mid\int_{{x}_{{P}} } ^{{x}_{{Q}} } \left({ax}^{\mathrm{2}} +{bx}+{c}\right){dx}\mid \\ $$$${A}=\mid\frac{{a}}{\mathrm{3}}\left({x}_{{Q}} ^{\mathrm{3}} −{x}_{{P}} ^{\mathrm{3}} \right)+\frac{{b}}{\mathrm{2}}\left({x}_{{Q}} ^{\mathrm{2}} −{x}_{{P}} ^{\mathrm{2}} \right)+{c}\left({x}_{{Q}} −{x}_{{P}} \right)\mid \\ $$$${A}=\mid\left\{\frac{{a}}{\mathrm{3}}\left({x}_{{Q}} ^{\mathrm{2}} +{x}_{{P}} {x}_{{Q}} +{x}_{{P}} ^{\mathrm{2}} \right)+\frac{{b}}{\mathrm{2}}\left({x}_{{Q}} +{x}_{{P}} \right)+{c}\right\}\left({x}_{{Q}} −{x}_{{P}} \right)\mid \\ $$$${A}=\mid\left\{\frac{{a}}{\mathrm{3}}\left[\left({x}_{{P}} +{x}_{{Q}} \right)^{\mathrm{2}} −{x}_{{P}} {x}_{{Q}} \right]+\frac{{b}}{\mathrm{2}}\left({x}_{{Q}} +{x}_{{P}} \right)+{c}\right\}\left({x}_{{Q}} −{x}_{{P}} \right)\mid \\ $$$$ \\ $$$${since}\:{x}_{{P}} \:{and}\:{x}_{{Q}} \:{are}\:{the}\:{roots}\:{of}\:{eqn}. \\ $$$${ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$${we}\:{have} \\ $$$${D}={b}^{\mathrm{2}} −\mathrm{4}{ac}\:\left({usually}\:{we}\:{use}\:\Delta\:{instead}\:{of}\:{D},\right. \\ $$$$\left.{here}\:{i}\:{use}\:{D}\:{because}\:{i}\:{have}\:{used}\:\Delta\:{above}\right) \\ $$$${x}_{{P}} +{x}_{{Q}} =−\frac{{b}}{{a}} \\ $$$${x}_{{P}} {x}_{{Q}} =\frac{{c}}{{a}} \\ $$$${x}_{{Q}} −{x}_{{P}} =\sqrt{\left({x}_{{Q}} +{x}_{{P}} \right)^{\mathrm{2}} −\mathrm{4}{x}_{{P}} {x}_{{Q}} }=\sqrt{\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\frac{\mathrm{4}{c}}{{a}}}=\frac{\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{{a}}=\frac{\sqrt{\delta}}{{a}} \\ $$$${A}=\mid\left\{\frac{{a}}{\mathrm{3}}\left[\left(−\frac{{b}}{{a}}\right)^{\mathrm{2}} −\frac{{c}}{{a}}\right]+\frac{{b}}{\mathrm{2}}\left(−\frac{{b}}{{a}}\right)+{c}\right\}\frac{\sqrt{{D}}}{{a}}\mid \\ $$$${A}=\mid\left(−{b}^{\mathrm{2}} +\mathrm{4}{ac}\right)\frac{\sqrt{{D}}}{\mathrm{6}{a}^{\mathrm{2}} }\mid \\ $$$${A}=\left({b}^{\mathrm{2}} −\mathrm{4}{ac}\right)\frac{\sqrt{{D}}}{\mathrm{6}{a}^{\mathrm{2}} } \\ $$$$\Rightarrow{A}=\frac{{D}\sqrt{{D}}}{\mathrm{6}{a}^{\mathrm{2}} }\:{with}\:{D}={b}^{\mathrm{2}} −\mathrm{4}{ac} \\ $$
Commented by mr W last updated on 19/Apr/20

$${i}\:{know}\:{jagoll}\:{sir}\:{uses}\:{this}\:{formula}.\: \\ $$$${here}\:{i}\:{just}\:{wanted}\:{to}\:{show}\:{how}\:{the} \\ $$$${formula}\:{comes}.\:{i}\:{think}\:{people}\:{apply} \\ $$$${better},\:{if}\:{they}\:{understand}.\:{that}'{s}\:{why} \\ $$$${i}\:{not}\:{only}\:{want}\:{to}\:{share}\:{the}\:{formula}, \\ $$$${but}\:{also}\:{to}\:{tell}\:{why}. \\ $$
Commented by jagoll last updated on 19/Apr/20

$$\mathrm{yes}\:\mathrm{sir}\:\mathrm{thank}\:\mathrm{you} \\ $$
Commented by I want to learn more last updated on 19/Apr/20

$$\mathrm{It}\:\mathrm{really}\:\mathrm{helped}\:\mathrm{me}\:\mathrm{sir}.\:\mathrm{More}\:\mathrm{knowledge}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
Commented by M±th+et£s last updated on 19/Apr/20
$${this}\:{is}\:{verry}\:{usefull}\:{for}\:{me}\:{god}\:{bless} \\ $$$${you}\:{sir}. \\ $$
Commented by otchereabdullai@gmail.com last updated on 19/Apr/20

$$\mathrm{wonderful} \\ $$
Commented by Coronavirus last updated on 27/Jun/20
thanks so much sir
