Question Number 89804 by peter frank last updated on 19/Apr/20
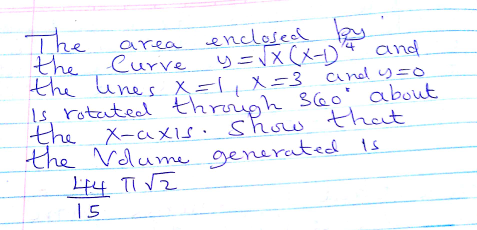
Answered by jagoll last updated on 19/Apr/20
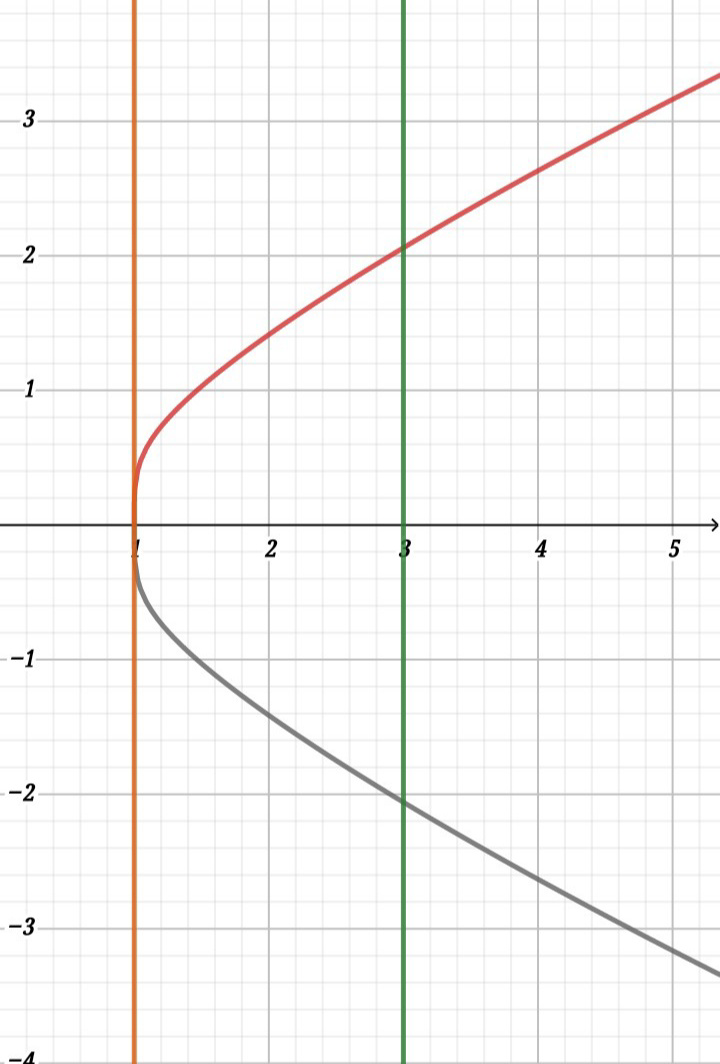
Commented by jagoll last updated on 19/Apr/20
![vol = π ∫_1 ^3 ((√x) ((x−1))^(1/(4 )) )^2 dx = π ∫_1 ^3 (x(√(x−1))) dx = π [ ((2x(x−1)^(3/2) )/3)− ((4(x−1)^(5/2) )/(15)) ]^3 _( 1) = π [ 4(√2) − ((16(√2))/(15)) ] = ((44π(√2))/(15))](https://www.tinkutara.com/question/Q89819.png)
$$\mathrm{vol}\:=\:\pi\:\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\:\left(\sqrt{\mathrm{x}}\:\sqrt[{\mathrm{4}\:\:}]{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{2}} \:\mathrm{dx} \\ $$$$=\:\pi\:\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\:\left(\mathrm{x}\sqrt{\mathrm{x}−\mathrm{1}}\right)\:\mathrm{dx} \\ $$$$=\:\pi\:\left[\:\frac{\mathrm{2x}\left(\mathrm{x}−\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}}−\:\frac{\mathrm{4}\left(\mathrm{x}−\mathrm{1}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} }{\mathrm{15}}\:\underset{\:\:\mathrm{1}} {\right]}^{\mathrm{3}} \\ $$$$=\:\pi\:\left[\:\mathrm{4}\sqrt{\mathrm{2}}\:−\:\frac{\mathrm{16}\sqrt{\mathrm{2}}}{\mathrm{15}}\:\right]\:=\:\frac{\mathrm{44}\pi\sqrt{\mathrm{2}}}{\mathrm{15}} \\ $$$$ \\ $$
Commented by peter frank last updated on 19/Apr/20

$${thank}\:{you} \\ $$
Commented by peter frank last updated on 19/Apr/20

$${why}\:{y}=\mathrm{0}\:{excluded} \\ $$
Commented by jagoll last updated on 19/Apr/20
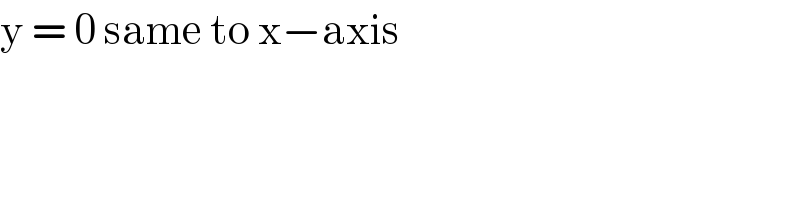
$$\mathrm{y}\:=\:\mathrm{0}\:\mathrm{same}\:\mathrm{to}\:\mathrm{x}−\mathrm{axis}\: \\ $$
