Question Number 89829 by student work last updated on 19/Apr/20

Commented by MJS last updated on 19/Apr/20
English please / Français s'il vous plaît
Commented by student work last updated on 19/Apr/20
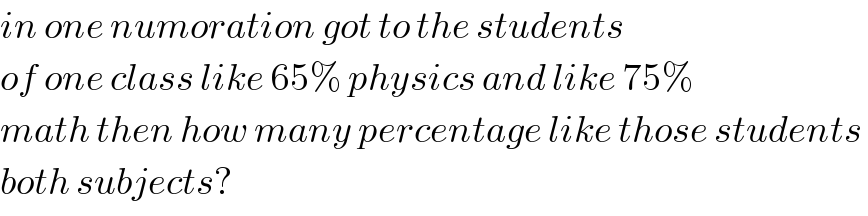
$${in}\:{one}\:{numoration}\:{got}\:{to}\:{the}\:{students}\: \\ $$$${of}\:{one}\:{class}\:{like}\:\mathrm{65\%}\:{physics}\:{and}\:{like}\:\mathrm{75\%} \\ $$$${math}\:{then}\:{how}\:{many}\:{percentage}\:{like}\:{those}\:{students}\: \\ $$$${both}\:{subjects}? \\ $$
Commented by john santu last updated on 19/Apr/20
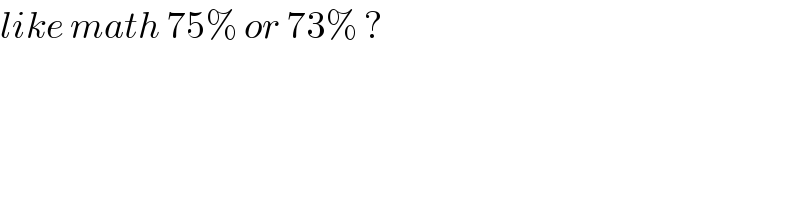
$${like}\:{math}\:\mathrm{75\%}\:{or}\:\mathrm{73\%}\:? \\ $$
Commented by john santu last updated on 19/Apr/20
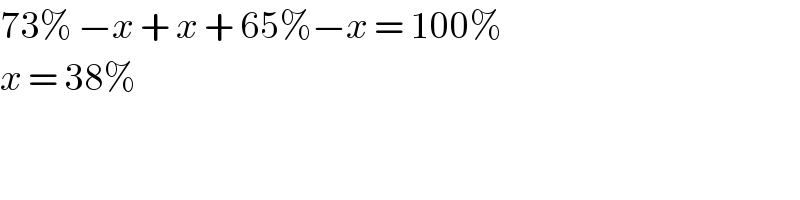
$$\mathrm{73\%}\:−{x}\:+\:{x}\:+\:\mathrm{65\%}−{x}\:=\:\mathrm{100\%} \\ $$$${x}\:=\:\mathrm{38\%}\: \\ $$$$ \\ $$
Commented by john santu last updated on 19/Apr/20

$${ans}\::\:\mathrm{38\%} \\ $$
Commented by student work last updated on 19/Apr/20

$$\mathrm{73} \\ $$
Commented by student work last updated on 19/Apr/20

$${is}\:{it}\:{formulla}? \\ $$
Commented by john santu last updated on 19/Apr/20
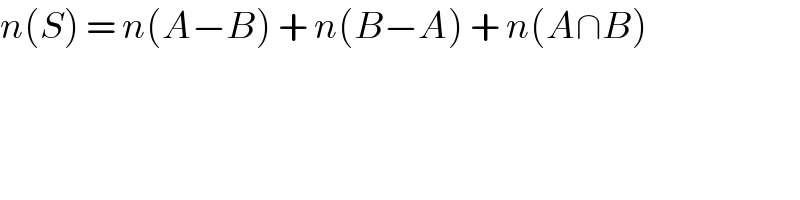
$${n}\left({S}\right)\:=\:{n}\left({A}−{B}\right)\:+\:{n}\left({B}−{A}\right)\:+\:{n}\left({A}\cap{B}\right) \\ $$
Commented by mr W last updated on 19/Apr/20

$${to}\:{be}\:{exact},\:{we}\:{can}\:{only}\:{say}\:{at}\:{least} \\ $$$$\mathrm{38\%}\:{like}\:{both}\:{subjects},\:{because}\:{there} \\ $$$${are}\:{also}\:{students}\:{who}\:{like}\:{none}\:{of} \\ $$$${both}\:{subjects}.\: \\ $$$${therefore}\:{there}\:{is}\:{no}\:{unique}\:{solution}! \\ $$$$ \\ $$$${this}\:{is}\:{correct}: \\ $$$$\mathrm{27\%}\:{like}\:{only}\:{physics} \\ $$$$\mathrm{35\%}\:{like}\:{only}\:{mathematics} \\ $$$$\mathrm{38\%}\:{like}\:{both}\:{subjects} \\ $$$$\mathrm{0\%}\:{like}\:{none}\:\left({e}.{g}.\:{in}\:{your}\:{school}\right) \\ $$$$ \\ $$$${but}\:{this}\:{is}\:{also}\:{correct}: \\ $$$$\mathrm{17\%}\:{like}\:{only}\:{physics} \\ $$$$\mathrm{25\%}\:{like}\:{only}\:{mathematics} \\ $$$$\mathrm{48\%}\:{like}\:{both}\:{subjects} \\ $$$$\mathrm{10\%}\:{like}\:{none}\:\left({e}.{g}.\:{in}\:{my}\:{school}\right) \\ $$$$ \\ $$$${such}\:{that}\:{there}\:{is}\:{an}\:{unique}\:{answer}, \\ $$$${it}\:{should}\:{be}\:{given}\:{that}\:{each}\:{student} \\ $$$${must}\:{like}\:{at}\:{least}\:{one}\:{subject}. \\ $$
