Question-89849

Question Number 89849 by ajfour last updated on 19/Apr/20

Commented by ajfour last updated on 19/Apr/20

$${Find}\:{maximum}\:{area}\:{of}\:\bigtriangleup{PQR} \\ $$$${in}\:{terms}\:{of}\:{ellipse}\:{parameters}\:{a},{b}. \\ $$$${or}\:\:{find}\:{side}\:{of}\:\bigtriangleup{PQR}\:{when} \\ $$$${it}\:{is}\:{equilateral}. \\ $$

Answered by mr W last updated on 19/Apr/20

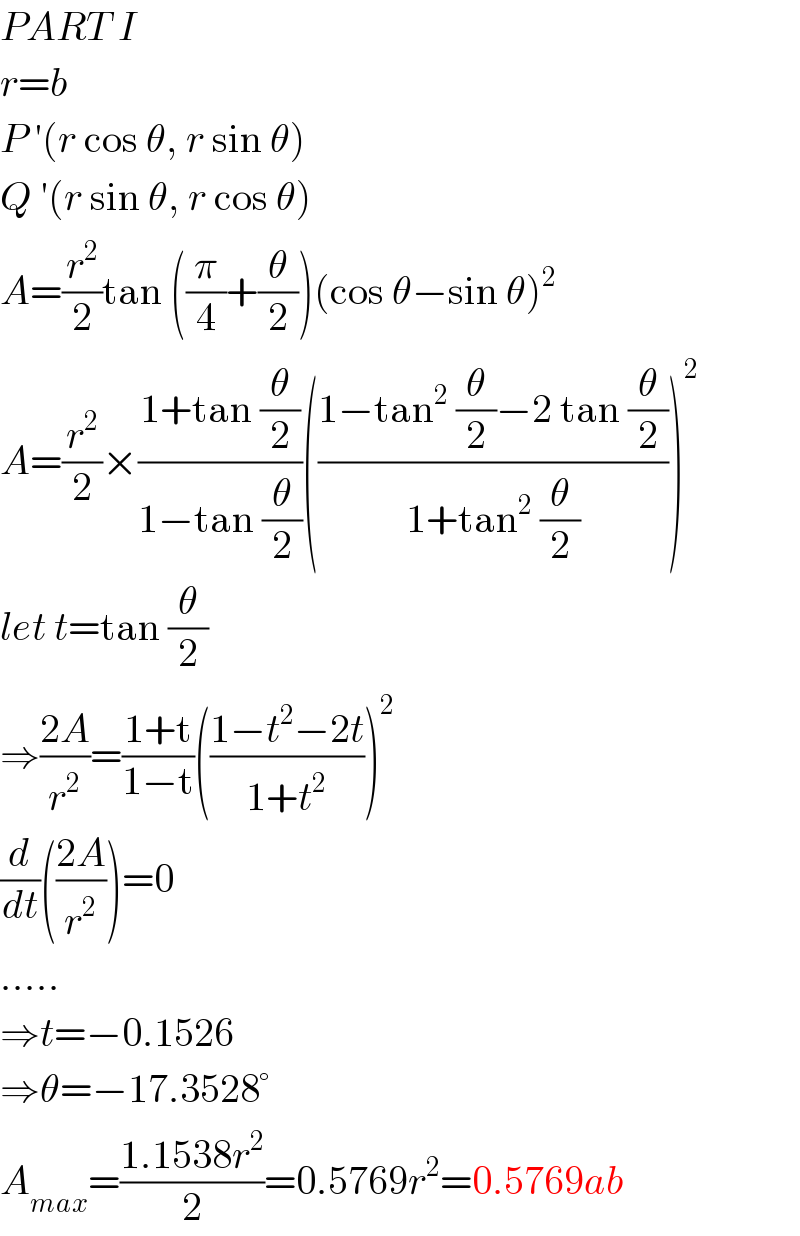
$${PART}\:{I} \\ $$$${r}={b} \\ $$$${P}\:'\left({r}\:\mathrm{cos}\:\theta,\:{r}\:\mathrm{sin}\:\theta\right) \\ $$$${Q}\:'\left({r}\:\mathrm{sin}\:\theta,\:{r}\:\mathrm{cos}\:\theta\right) \\ $$$${A}=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}+\frac{\theta}{\mathrm{2}}\right)\left(\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$${A}=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}×\frac{\mathrm{1}+\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}\left(\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}−\mathrm{2}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}\right)^{\mathrm{2}} \\ $$$${let}\:{t}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{2}{A}}{{r}^{\mathrm{2}} }=\frac{\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}}\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} −\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\frac{{d}}{{dt}}\left(\frac{\mathrm{2}{A}}{{r}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$….. \\ $$$$\Rightarrow{t}=−\mathrm{0}.\mathrm{1526} \\ $$$$\Rightarrow\theta=−\mathrm{17}.\mathrm{3528}° \\ $$$${A}_{{max}} =\frac{\mathrm{1}.\mathrm{1538}{r}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{0}.\mathrm{5769}{r}^{\mathrm{2}} =\mathrm{0}.\mathrm{5769}{ab} \\ $$

Commented by mr W last updated on 19/Apr/20

Commented by ajfour last updated on 20/Apr/20

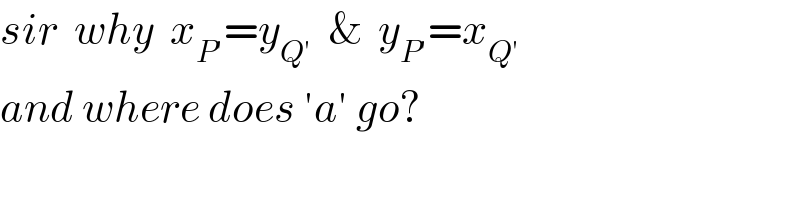
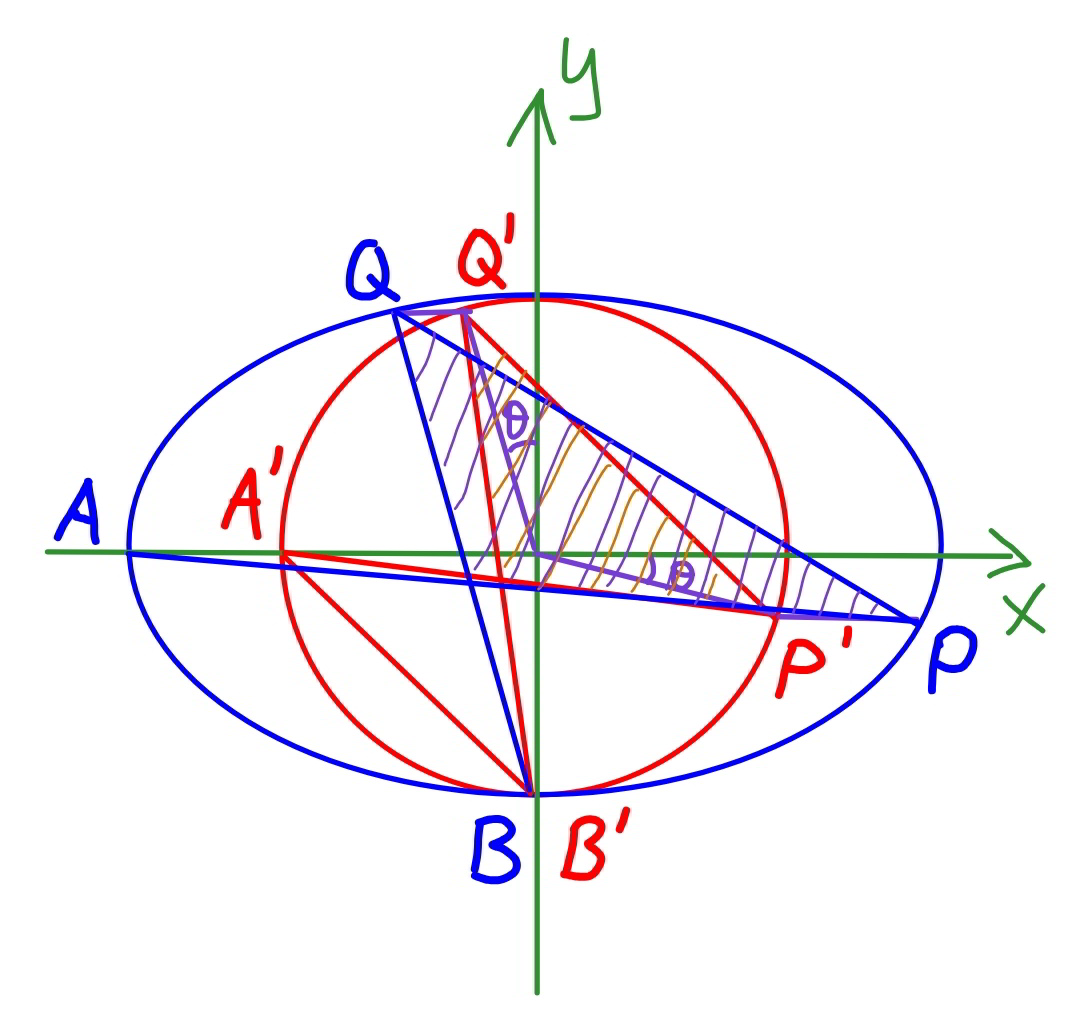
$${sir}\:\:{why}\:\:{x}_{{P}'} ={y}_{{Q}'} \:\:\&\:\:{y}_{{P}'} ={x}_{{Q}'} \\ $$$${and}\:{where}\:{does}\:'{a}'\:{go}? \\ $$

Commented by mr W last updated on 20/Apr/20

$${in}\:{case}\:{of}\:{circle}\:{we}\:{use}\:{the}\:{symmetry} \\ $$$${for}\:{the}\:{max}.\:{area}. \\ $$$${in}\:{case}\:{of}\:{ellipse}\:{we}\:{only}\:{need}\:{to} \\ $$$${stretch}\:{the}\:{circle}\:{in}\:{x}−{direction}\:{in} \\ $$$${ratio}\:\frac{{a}}{{r}},\:{i}.{e}.\:\frac{{a}}{{b}}. \\ $$

Answered by mr W last updated on 19/Apr/20

Commented by mr W last updated on 19/Apr/20

$${PART}\:{II} \\ $$$${the}\:{point}\:{R}\:{must}\:{lie}\:{on}\:{the}\:{green}\:{circle} \\ $$$${with}\:{center}\:{at}\:{C}. \\ $$$${let}\:\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{{b}}{{a}},\:\mu=\frac{{b}}{{a}} \\ $$$${AC}=\frac{{AB}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{30}°}=\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{3}}} \\ $$$${x}_{{C}} =−{a}+{AC}\:\:\mathrm{cos}\:\left(\mathrm{30}°−\alpha\right) \\ $$$${x}_{{C}} =−{a}+\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{3}}}\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{{a}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{{b}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right) \\ $$$$\Rightarrow{x}_{{C}} =−\frac{\mathrm{1}}{\mathrm{2}}\:\left({a}−\frac{{b}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$${y}_{{C}} ={AC}\:\mathrm{sin}\:\left(\mathrm{30}°−\alpha\right)=\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{3}}}\left(\frac{\mathrm{1}}{\mathrm{2}}×\frac{{a}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{{b}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right) \\ $$$$\Rightarrow{y}_{{C}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{a}}{\:\sqrt{\mathrm{3}}}−{b}\right) \\ $$$$ \\ $$$${eqn}.\:{of}\:{green}\:{circle}: \\ $$$$\left[{x}+\frac{\mathrm{1}}{\mathrm{2}}\left({a}−\frac{{b}}{\:\sqrt{\mathrm{3}}}\right)\right]^{\mathrm{2}} +\left[{y}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{a}}{\:\sqrt{\mathrm{3}}}−{b}\right)\right]^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{3}} \\ $$$${or} \\ $$$${x}_{{R}} =−\frac{\mathrm{1}}{\mathrm{2}}\left({a}−\frac{{b}}{\:\sqrt{\mathrm{3}}}\right)+\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{3}}}\:\mathrm{cos}\:\theta \\ $$$${y}_{{R}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{a}}{\:\sqrt{\mathrm{3}}}−{b}\right)+\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{3}}}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\frac{{x}_{{R}} }{{a}}=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mu}{\:\sqrt{\mathrm{3}}}\right)+\sqrt{\frac{\mathrm{1}+\mu^{\mathrm{2}} }{\mathrm{3}}}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\frac{{y}_{{R}} }{{a}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}−\mu\right)+\sqrt{\frac{\mathrm{1}+\mu^{\mathrm{2}} }{\mathrm{3}}}\:\mathrm{sin}\:\theta \\ $$$$ \\ $$$${eqn}.\:{of}\:{AR}: \\ $$$${y}=\frac{{a}−\sqrt{\mathrm{3}}{b}+\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\mathrm{sin}\:\theta}{\:\sqrt{\mathrm{3}}{a}+{b}+\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\mathrm{cos}\:\theta}\left({x}+{a}\right) \\ $$$${y}=\frac{\mathrm{1}−\sqrt{\mathrm{3}}\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{sin}\:\theta}{\:\sqrt{\mathrm{3}}+\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{cos}\:\theta}\left({x}+{a}\right) \\ $$$${intersection}\:{point}\:{P}: \\ $$$${y}_{{P}} =\frac{\mathrm{1}−\sqrt{\mathrm{3}}\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{sin}\:\theta}{\:\sqrt{\mathrm{3}}+\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{cos}\:\theta}\left({x}_{{P}} +{a}\right) \\ $$$$\left(\frac{{x}_{{P}} }{{a}}\right)^{\mathrm{2}} +\left(\frac{{y}_{{P}} }{{b}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\left(\frac{\mathrm{1}−\sqrt{\mathrm{3}}\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{sin}\:\theta}{\:\sqrt{\mathrm{3}}+\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \left(\mathrm{1}+\frac{{x}_{{P}} }{{a}}\right)^{\mathrm{2}} =\mu^{\mathrm{2}} \left[\mathrm{1}−\left(\frac{{x}_{{P}} }{{a}}\right)^{\mathrm{2}} \right] \\ $$$$\left(\frac{\mathrm{1}−\sqrt{\mathrm{3}}\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{sin}\:\theta}{\:\sqrt{\mathrm{3}}+\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \left(\mathrm{1}+\frac{{x}_{{P}} }{{a}}\right)=\mu^{\mathrm{2}} \left(\mathrm{1}−\frac{{x}_{{P}} }{{a}}\right) \\ $$$$\Rightarrow\frac{{x}_{{P}} }{{a}}=\frac{\mu^{\mathrm{2}} −\left(\frac{\mathrm{1}−\sqrt{\mathrm{3}}\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{sin}\:\theta}{\:\sqrt{\mathrm{3}}+\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{cos}\:\theta}\right)^{\mathrm{2}} }{\mu^{\mathrm{2}} +\left(\frac{\mathrm{1}−\sqrt{\mathrm{3}}\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{sin}\:\theta}{\:\sqrt{\mathrm{3}}+\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{cos}\:\theta}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{y}_{{P}} }{{a}}=\left(\frac{\mathrm{1}−\sqrt{\mathrm{3}}\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{sin}\:\theta}{\:\sqrt{\mathrm{3}}+\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{cos}\:\theta}\right)\left(\mathrm{1}+\frac{{x}_{{P}} }{{a}}\right) \\ $$$$\frac{{PR}^{\mathrm{2}} }{{a}^{\mathrm{2}} }=\left(\frac{{x}_{{P}} }{{a}}−\frac{{x}_{{R}} }{{a}}\right)^{\mathrm{2}} +\left(\frac{{y}_{{P}} }{{a}}−\frac{{y}_{{R}} }{{a}}\right)^{\mathrm{2}} \\ $$$$ \\ $$$${eqn}.\:{of}\:{BR}: \\ $$$$\frac{{y}+{b}}{{y}_{{R}} +{b}}=\frac{{x}}{{x}_{{R}} } \\ $$$${y}=−{b}+\frac{{a}+\sqrt{\mathrm{3}}{b}+\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\mathrm{sin}\:\theta}{−\sqrt{\mathrm{3}}{a}+{b}+\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\mathrm{cos}\:\theta}{x} \\ $$$${y}=−{b}+\frac{\mathrm{1}+\sqrt{\mathrm{3}}\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{sin}\:\theta}{−\sqrt{\mathrm{3}}+\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{cos}\:\theta}{x} \\ $$$${intersection}\:{point}\:{Q}: \\ $$$${y}_{{Q}} =−{b}+\frac{\mathrm{1}+\sqrt{\mathrm{3}}\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{sin}\:\theta}{−\sqrt{\mathrm{3}}+\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{cos}\:\theta}{x}_{{Q}} \\ $$$${x}_{{Q}} =\frac{−\sqrt{\mathrm{3}}+\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{cos}\:\theta}{\mathrm{1}+\sqrt{\mathrm{3}}\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{sin}\:\theta}\left({y}_{{Q}} +{b}\right) \\ $$$$\left(\frac{{x}_{{Q}} }{{a}}\right)^{\mathrm{2}} +\left(\frac{{y}_{{Q}} }{{b}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mu^{\mathrm{2}} \left(\frac{−\sqrt{\mathrm{3}}+\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{cos}\:\theta}{\mathrm{1}+\sqrt{\mathrm{3}}\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{sin}\:\theta}\right)^{\mathrm{2}} \left(\frac{{y}_{{Q}} }{{a}}+\mu\right)^{\mathrm{2}} +\left(\frac{{y}_{{Q}} }{{a}}\right)^{\mathrm{2}} =\mu^{\mathrm{2}} \\ $$$$\mu^{\mathrm{2}} \left(\frac{−\sqrt{\mathrm{3}}+\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{cos}\:\theta}{\mathrm{1}+\sqrt{\mathrm{3}}\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{sin}\:\theta}\right)^{\mathrm{2}} \left(\frac{{y}_{{Q}} }{{a}}+\mu\right)=\mu−\frac{{y}_{{Q}} }{{a}} \\ $$$$\Rightarrow\frac{{y}_{{Q}} }{{a}}=\frac{\mu\left[\mathrm{1}−\mu^{\mathrm{2}} \left(\frac{−\sqrt{\mathrm{3}}+\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{cos}\:\theta}{\mathrm{1}+\sqrt{\mathrm{3}}\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{sin}\:\theta}\right)^{\mathrm{2}} \right]}{\mathrm{1}+\mu^{\mathrm{2}} \left(\frac{−\sqrt{\mathrm{3}}+\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{cos}\:\theta}{\mathrm{1}+\sqrt{\mathrm{3}}\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{sin}\:\theta}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{x}_{{Q}} }{{a}}=\left(\frac{−\sqrt{\mathrm{3}}+\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{cos}\:\theta}{\mathrm{1}+\sqrt{\mathrm{3}}\mu+\mathrm{2}\sqrt{\mathrm{1}+\mu^{\mathrm{2}} }\:\mathrm{sin}\:\theta}\right)\left(\frac{{y}_{{Q}} }{{a}}+\mu\right) \\ $$$$\frac{{QR}^{\mathrm{2}} }{{a}^{\mathrm{2}} }=\left(\frac{{x}_{{Q}} }{{a}}−\frac{{x}_{{R}} }{{a}}\right)^{\mathrm{2}} +\left(\frac{{y}_{{Q}} }{{a}}−\frac{{y}_{{R}} }{{a}}\right)^{\mathrm{2}} \\ $$$$ \\ $$$${such}\:{that}\:\Delta{PQR}\:{is}\:{equilateral}, \\ $$$${PR}={QR} \\ $$$$\frac{{PR}^{\mathrm{2}} }{{a}^{\mathrm{2}} }=\frac{{QR}^{\mathrm{2}} }{{a}^{\mathrm{2}} } \\ $$

Commented by mr W last updated on 19/Apr/20

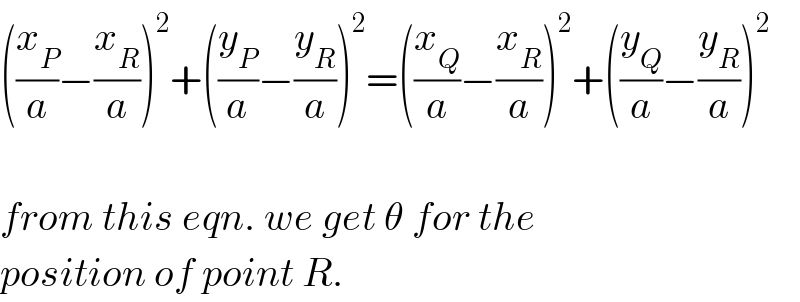
$$\left(\frac{{x}_{{P}} }{{a}}−\frac{{x}_{{R}} }{{a}}\right)^{\mathrm{2}} +\left(\frac{{y}_{{P}} }{{a}}−\frac{{y}_{{R}} }{{a}}\right)^{\mathrm{2}} =\left(\frac{{x}_{{Q}} }{{a}}−\frac{{x}_{{R}} }{{a}}\right)^{\mathrm{2}} +\left(\frac{{y}_{{Q}} }{{a}}−\frac{{y}_{{R}} }{{a}}\right)^{\mathrm{2}} \\ $$$$ \\ $$$${from}\:{this}\:{eqn}.\:{we}\:{get}\:\theta\:{for}\:{the} \\ $$$${position}\:{of}\:{point}\:{R}. \\ $$

Commented by mr W last updated on 19/Apr/20

Commented by mr W last updated on 20/Apr/20

Commented by mr W last updated on 20/Apr/20

Commented by mr W last updated on 20/Apr/20

Commented by mr W last updated on 21/Apr/20

Answered by ajfour last updated on 20/Apr/20

Commented by ajfour last updated on 20/Apr/20

$${let}\:\:{R}\left({h},{k}\right) \\ $$$${Eq}.\:{AP}:\:\:{y}=\frac{{k}\left({x}+{a}\right)}{{h}+{a}} \\ $$$${b}^{\mathrm{2}} {x}^{\mathrm{2}} +\frac{{k}^{\mathrm{2}} \left({x}+{a}\right)^{\mathrm{2}} {a}^{\mathrm{2}} }{\left({h}+{a}\right)^{\mathrm{2}} }={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\left({h}+{a}\right)^{\mathrm{2}} {b}^{\mathrm{2}} {x}^{\mathrm{2}} +{k}^{\mathrm{2}} {a}^{\mathrm{2}} \left({x}+{a}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({h}+{a}\right)^{\mathrm{2}} \\ $$$${roots}\:{are}\:{x}_{{P}} \:,\:−{a} \\ $$$$\Rightarrow\:\:−{ax}_{{P}} =\:\frac{{a}^{\mathrm{2}} \left[{a}^{\mathrm{2}} {k}^{\mathrm{2}} −{b}^{\mathrm{2}} \left({h}+{a}\right)^{\mathrm{2}} \right]}{{b}^{\mathrm{2}} \left({h}+{a}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} {a}^{\mathrm{2}} }\: \\ $$$$\:\:{x}_{{P}} =\frac{{a}\left[{b}^{\mathrm{2}} \left({h}+{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} {k}^{\mathrm{2}} \right]}{{b}^{\mathrm{2}} \left({h}+{a}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} {a}^{\mathrm{2}} }\:\:\:…\left({I}\right) \\ $$$${Eq}.\:{of}\:{BQ}: \\ $$$$\:\:{y}=\left(\frac{{k}+{b}}{{h}}\right){x}−{b} \\ $$$${b}^{\mathrm{2}} {h}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} \left[\left({k}+{b}\right){x}−{bh}\right]^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} {h}^{\mathrm{2}} \\ $$$$\:\:{roots}\:{are}\:\:{x}=\mathrm{0},\:{x}_{{Q}} \\ $$$$\:\:{x}_{{Q}} =\:\frac{\mathrm{2}{a}^{\mathrm{2}} {bh}\left({k}+{b}\right)}{{b}^{\mathrm{2}} {h}^{\mathrm{2}} +{a}^{\mathrm{2}} \left({k}+{b}\right)^{\mathrm{2}} }\:\:\:…\left({II}\right) \\ $$$$\frac{\frac{{k}+{b}}{{h}}−\frac{{k}}{{h}+{a}}}{\mathrm{1}+\left(\frac{{k}+{b}}{{h}}\right)\left(\frac{{k}}{{h}+{a}}\right)}=\sqrt{\mathrm{3}}\:\:\:\:….\left({III}\right) \\ $$$${slope}\:{of}\:{PQ}: \\ $$$$\:\:\:\frac{{y}_{{Q}} −{y}_{{P}} }{{x}_{{P}} −{x}_{{Q}} }=\frac{\sqrt{\mathrm{3}}−\frac{{k}}{{h}+{a}}}{\mathrm{1}+\sqrt{\mathrm{3}}\left(\frac{{k}}{{h}+{a}}\right)}\:\:\:\:…\left({IV}\right) \\ $$$${let}\:\:\frac{{k}}{{h}+{a}}={p}\:\:,\:\:\frac{{k}+{b}}{{h}}={q} \\ $$$${x}_{{P}} =\frac{{a}\left[{b}^{\mathrm{2}} \left({h}+{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} {k}^{\mathrm{2}} \right]}{{b}^{\mathrm{2}} \left({h}+{a}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} {a}^{\mathrm{2}} } \\ $$$$\:\:\:=\:\frac{{a}\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} {p}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} +{a}^{\mathrm{2}} {p}^{\mathrm{2}} } \\ $$$$\:\:{x}_{{Q}} =\frac{\mathrm{2}{a}^{\mathrm{2}} {bh}\left({k}+{b}\right)}{{b}^{\mathrm{2}} {h}^{\mathrm{2}} +{a}^{\mathrm{2}} \left({k}+{b}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:=\:\frac{\mathrm{2}{a}^{\mathrm{2}} {bq}}{{b}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} } \\ $$$${y}_{{P}} ={p}\left({x}_{{P}} +{a}\right)=\frac{{p}\left(\mathrm{2}{ab}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} +{a}^{\mathrm{2}} {p}^{\mathrm{2}} } \\ $$$${y}_{{Q}} ={qx}_{{Q}} −{b}\:=\:\frac{\mathrm{2}{a}^{\mathrm{2}} {bq}^{\mathrm{2}} }{{b}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} }−{b} \\ $$$$\:\:\:\:=\frac{{b}\left({a}^{\mathrm{2}} {q}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} } \\ $$$$\:\frac{\frac{{b}\left({a}^{\mathrm{2}} {q}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} }−\frac{{p}\left(\mathrm{2}{ab}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} +{a}^{\mathrm{2}} {p}^{\mathrm{2}} }}{\frac{{a}\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} {p}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} +{a}^{\mathrm{2}} {p}^{\mathrm{2}} }−\frac{\mathrm{2}{a}^{\mathrm{2}} {bq}}{{b}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} }}=\frac{\sqrt{\mathrm{3}}−{p}}{\mathrm{1}+{p}\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……\left({i}\right) \\ $$$${And}\:\:\:\frac{{q}−{p}}{\mathrm{1}+{pq}}=\sqrt{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:…….\left({ii}\right) \\ $$$$\frac{{b}\left({a}^{\mathrm{2}} {q}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} +{a}^{\mathrm{2}} {p}^{\mathrm{2}} \right)−\mathrm{2}{ab}^{\mathrm{2}} {p}\left({b}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} \right)}{{a}\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} {p}^{\mathrm{2}} \right)\left({b}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} \right)+\mathrm{2}{a}^{\mathrm{2}} {bq}\left({b}^{\mathrm{2}} +{a}^{\mathrm{2}} {p}^{\mathrm{2}} \right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\sqrt{\mathrm{3}}−{p}}{\mathrm{1}+{p}\sqrt{\mathrm{3}}}\: \\ $$$$…. \\ $$

Commented by mr W last updated on 20/Apr/20

$${you}\:{can}\:{get}\:{also}\:{a}\:{final}\:{eqn}.\:{with}\:{one} \\ $$$${unknown}\:{in}\:{this}\:{way}. \\ $$

Commented by ajfour last updated on 21/Apr/20

$${I}\:{have}\:{a}\:{better}\:{way}\:{too},\:{Sir}, \\ $$$${but}\:{lets}\:{leave}\:{it}\:{here};\:{you} \\ $$$${solved}\:{it}\:{wonderfully},\:{both} \\ $$$${parts},\:\:\mathcal{T}{hanks}\:{a}\:{lot}! \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com