Question Number 89882 by student work last updated on 19/Apr/20

Answered by Joel578 last updated on 19/Apr/20

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}!\left(\mathrm{1}−\:{x}\:−\:\mathrm{1}\right)}{\left(\mathrm{2}{x}−\mathrm{1}\right){x}!}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{−{x}}{\mathrm{2}{x}−\mathrm{1}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by TANMAY PANACEA. last updated on 19/Apr/20
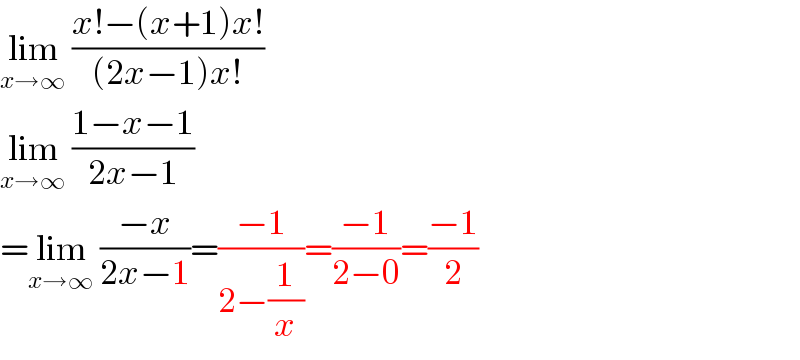
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}!−\left({x}+\mathrm{1}\right){x}!}{\left(\mathrm{2}{x}−\mathrm{1}\right){x}!} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}−{x}−\mathrm{1}}{\mathrm{2}{x}−\mathrm{1}} \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{−{x}}{\mathrm{2}{x}−\mathrm{1}}=\frac{−\mathrm{1}}{\mathrm{2}−\frac{\mathrm{1}}{{x}}}=\frac{−\mathrm{1}}{\mathrm{2}−\mathrm{0}}=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$
