Question Number 89913 by M±th+et£s last updated on 20/Apr/20

Commented by M±th+et£s last updated on 20/Apr/20

$${prove}\:{that} \\ $$
Answered by maths mind last updated on 20/Apr/20
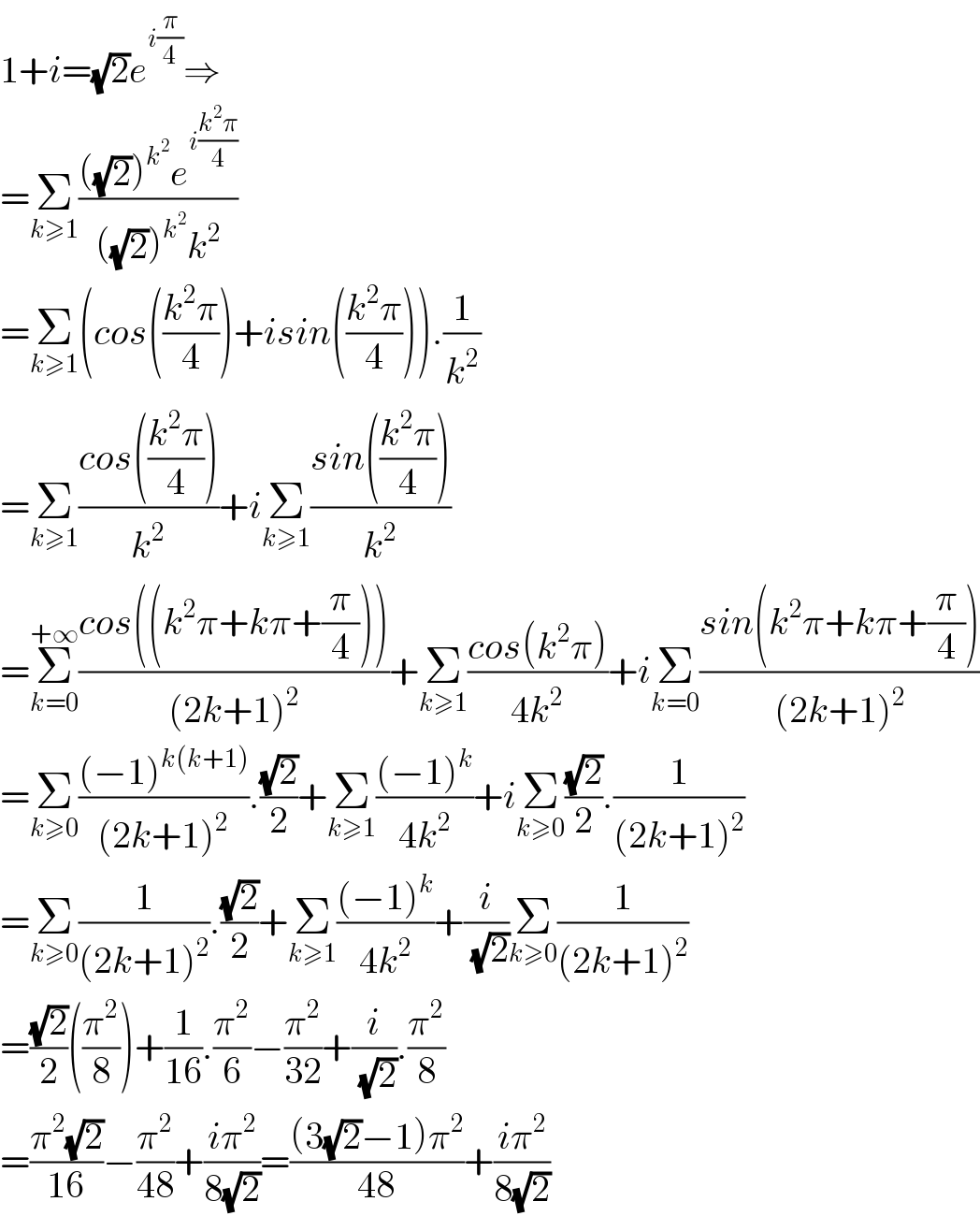
$$\mathrm{1}+{i}=\sqrt{\mathrm{2}}{e}^{{i}\frac{\pi}{\mathrm{4}}} \Rightarrow \\ $$$$=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(\sqrt{\mathrm{2}}\right)^{{k}^{\mathrm{2}} } {e}^{{i}\frac{{k}^{\mathrm{2}} \pi}{\mathrm{4}}} }{\left(\sqrt{\mathrm{2}}\right)^{{k}^{\mathrm{2}} } {k}^{\mathrm{2}} } \\ $$$$=\underset{{k}\geqslant\mathrm{1}} {\sum}\left({cos}\left(\frac{{k}^{\mathrm{2}} \pi}{\mathrm{4}}\right)+{isin}\left(\frac{{k}^{\mathrm{2}} \pi}{\mathrm{4}}\right)\right).\frac{\mathrm{1}}{{k}^{\mathrm{2}} } \\ $$$$=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{cos}\left(\frac{{k}^{\mathrm{2}} \pi}{\mathrm{4}}\right)}{{k}^{\mathrm{2}} }+{i}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{sin}\left(\frac{{k}^{\mathrm{2}} \pi}{\mathrm{4}}\right)}{{k}^{\mathrm{2}} } \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{{cos}\left(\left({k}^{\mathrm{2}} \pi+{k}\pi+\frac{\pi}{\mathrm{4}}\right)\right)}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{cos}\left({k}^{\mathrm{2}} \pi\right)}{\mathrm{4}{k}^{\mathrm{2}} }+{i}\underset{{k}=\mathrm{0}} {\sum}\frac{{sin}\left({k}^{\mathrm{2}} \pi+{k}\pi+\frac{\pi}{\mathrm{4}}\right)}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}\left({k}+\mathrm{1}\right)} }{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }.\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{4}{k}^{\mathrm{2}} }+{i}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}.\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }.\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{4}{k}^{\mathrm{2}} }+\frac{{i}}{\:\sqrt{\mathrm{2}}}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\right)+\frac{\mathrm{1}}{\mathrm{16}}.\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\frac{\pi^{\mathrm{2}} }{\mathrm{32}}+\frac{{i}}{\:\sqrt{\mathrm{2}}}.\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$=\frac{\pi^{\mathrm{2}} \sqrt{\mathrm{2}}}{\mathrm{16}}−\frac{\pi^{\mathrm{2}} }{\mathrm{48}}+\frac{{i}\pi^{\mathrm{2}} }{\mathrm{8}\sqrt{\mathrm{2}}}=\frac{\left(\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{1}\right)\pi^{\mathrm{2}} }{\mathrm{48}}+\frac{{i}\pi^{\mathrm{2}} }{\mathrm{8}\sqrt{\mathrm{2}}} \\ $$
Commented by M±th+et£s last updated on 20/Apr/20
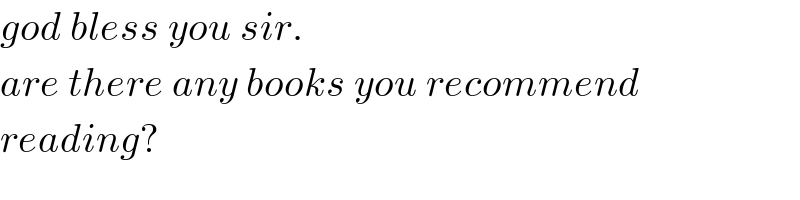
$${god}\:{bless}\:{you}\:{sir}. \\ $$$${are}\:{there}\:{any}\:{books}\:{you}\:{recommend} \\ $$$${reading}? \\ $$
Commented by maths mind last updated on 20/Apr/20

$${Almost}\:{impposible}\:{Series}\:{and}\:{integral}\: \\ $$$${i}\:{will}\:{chek}\:{the}\:{right}\:{titel}\:{and}\:{comback}\: \\ $$
Commented by M±th+et£s last updated on 20/Apr/20
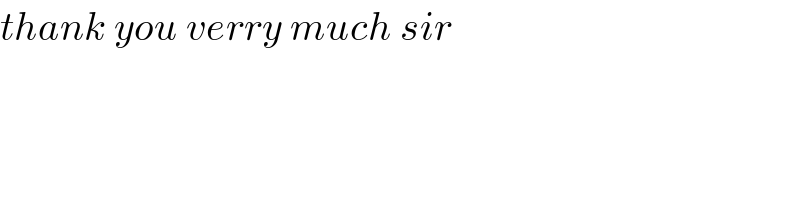
$${thank}\:{you}\:{verry}\:{much}\:{sir}\: \\ $$
Commented by M±th+et£s last updated on 20/Apr/20
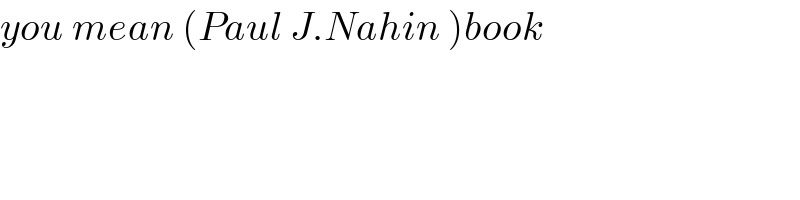
$${you}\:{mean}\:\left({Paul}\:{J}.{Nahin}\:\right){book} \\ $$
