Question Number 89922 by student work last updated on 20/Apr/20

Commented by john santu last updated on 20/Apr/20
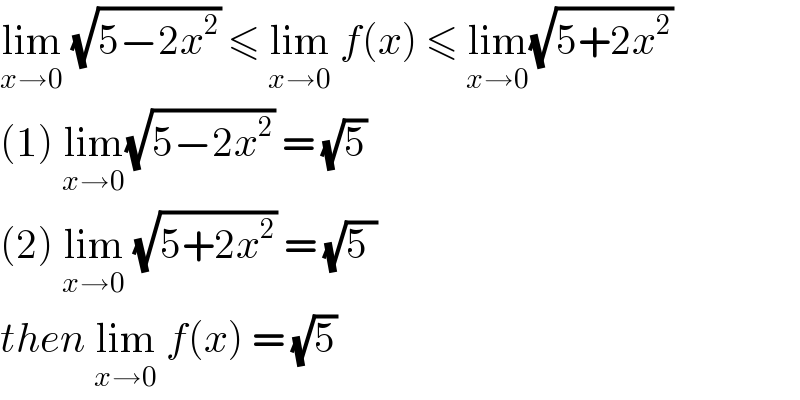
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt{\mathrm{5}−\mathrm{2}{x}^{\mathrm{2}} }\:\leqslant\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{f}\left({x}\right)\:\leqslant\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\sqrt{\mathrm{5}+\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\sqrt{\mathrm{5}−\mathrm{2}{x}^{\mathrm{2}} }\:=\:\sqrt{\mathrm{5}} \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt{\mathrm{5}+\mathrm{2}{x}^{\mathrm{2}} }\:=\:\sqrt{\mathrm{5}\:} \\ $$$${then}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{f}\left({x}\right)\:=\:\sqrt{\mathrm{5}}\: \\ $$
Commented by jagoll last updated on 20/Apr/20
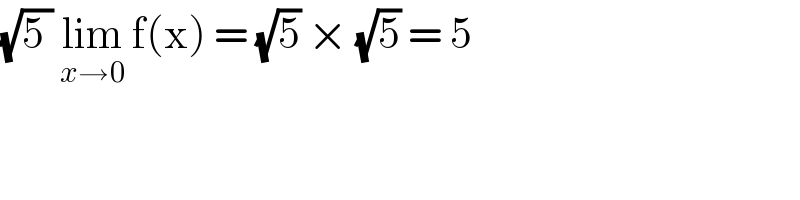
$$\sqrt{\mathrm{5}\:}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\sqrt{\mathrm{5}}\:×\:\sqrt{\mathrm{5}}\:=\:\mathrm{5} \\ $$
