Question Number 89928 by oustmuchiya@gmail.com last updated on 20/Apr/20
Answered by MJS last updated on 20/Apr/20
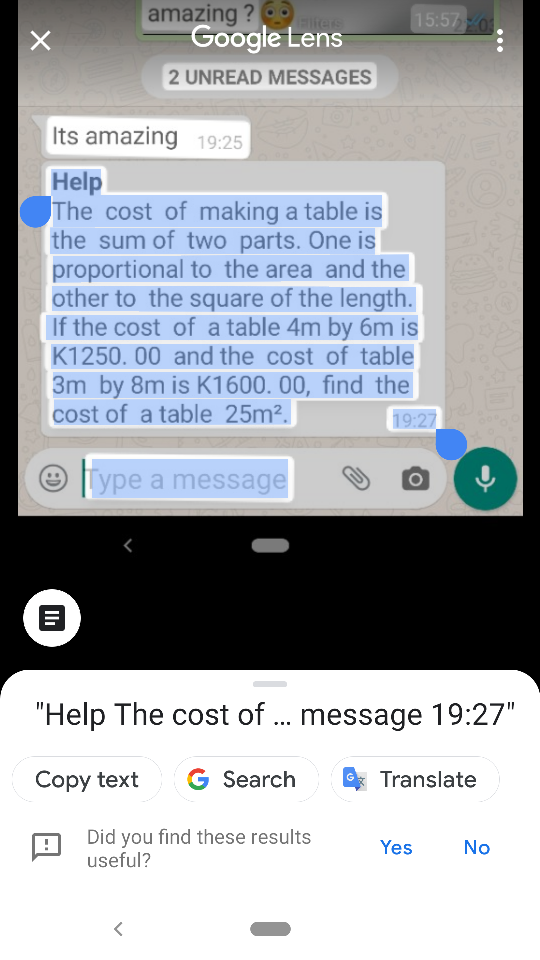
![area=a length=l cost=c c=xa+yl^2 1250=24x+36y 1600=24x+64y ⇒ x=((100)/3)∧y=((25)/2) c=((100)/3)a+((25)/2)l^2 if the table has 25m^2 ⇒ it′s 5×5m c=((100)/3)×25+((25)/2)×25=((6875)/6)≈1145.83 [if we allow l∉N we need more info]](https://www.tinkutara.com/question/Q89935.png)
$$\mathrm{area}={a} \\ $$$$\mathrm{length}={l} \\ $$$$\mathrm{cost}={c} \\ $$$${c}={xa}+{yl}^{\mathrm{2}} \\ $$$$\mathrm{1250}=\mathrm{24}{x}+\mathrm{36}{y} \\ $$$$\mathrm{1600}=\mathrm{24}{x}+\mathrm{64}{y} \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{100}}{\mathrm{3}}\wedge{y}=\frac{\mathrm{25}}{\mathrm{2}} \\ $$$${c}=\frac{\mathrm{100}}{\mathrm{3}}{a}+\frac{\mathrm{25}}{\mathrm{2}}{l}^{\mathrm{2}} \\ $$$$\mathrm{if}\:\mathrm{the}\:\mathrm{table}\:\mathrm{has}\:\mathrm{25m}^{\mathrm{2}} \:\Rightarrow\:\mathrm{it}'\mathrm{s}\:\mathrm{5}×\mathrm{5m} \\ $$$${c}=\frac{\mathrm{100}}{\mathrm{3}}×\mathrm{25}+\frac{\mathrm{25}}{\mathrm{2}}×\mathrm{25}=\frac{\mathrm{6875}}{\mathrm{6}}\approx\mathrm{1145}.\mathrm{83} \\ $$$$\left[\mathrm{if}\:\mathrm{we}\:\mathrm{allow}\:{l}\notin\mathbb{N}\:\mathrm{we}\:\mathrm{need}\:\mathrm{more}\:\mathrm{info}\right] \\ $$
Commented by jagoll last updated on 20/Apr/20
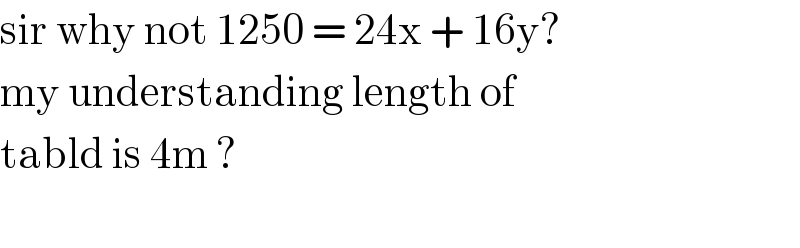
$$\mathrm{sir}\:\mathrm{why}\:\mathrm{not}\:\mathrm{1250}\:=\:\mathrm{24x}\:+\:\mathrm{16y}?\: \\ $$$$\mathrm{my}\:\mathrm{understanding}\:\mathrm{length}\:\mathrm{of}\: \\ $$$$\mathrm{tabld}\:\mathrm{is}\:\mathrm{4m}\:?\: \\ $$$$ \\ $$
Commented by jagoll last updated on 20/Apr/20
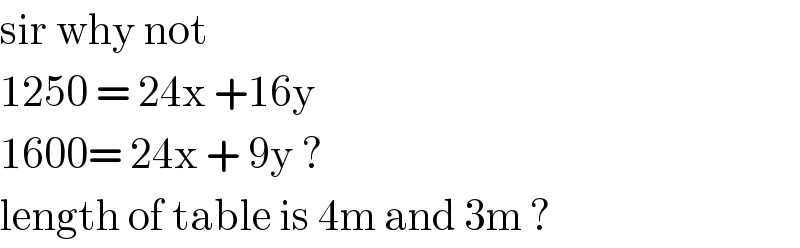
$$\mathrm{sir}\:\mathrm{why}\:\mathrm{not}\: \\ $$$$\mathrm{1250}\:=\:\mathrm{24x}\:+\mathrm{16y} \\ $$$$\mathrm{1600}=\:\mathrm{24x}\:+\:\mathrm{9y}\:? \\ $$$$\mathrm{length}\:\mathrm{of}\:\mathrm{table}\:\mathrm{is}\:\mathrm{4m}\:\mathrm{and}\:\mathrm{3m}\:? \\ $$
Commented by MJS last updated on 20/Apr/20

$$“\mathrm{length}''\:\mathrm{comes}\:\mathrm{from}\:“\mathrm{long}'';\:\mathrm{a}\:\mathrm{table}\:\mathrm{has}\:\mathrm{a} \\ $$$$\mathrm{long}\:\mathrm{and}\:\mathrm{a}\:\mathrm{short}\:\mathrm{side}\:\mathrm{if}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{square}.\:\mathrm{why} \\ $$$$\mathrm{would}\:\mathrm{you}\:\mathrm{call}\:\mathrm{the}\:\mathrm{short}\:\mathrm{side}\:“\mathrm{length}''? \\ $$
Commented by MJS last updated on 20/Apr/20

$$\mathrm{but}\:\mathrm{anyway},\:\mathrm{the}\:\mathrm{path}\:\mathrm{is}\:\mathrm{clear}… \\ $$
Commented by john santu last updated on 20/Apr/20

$${is}\:{not}\:{in}\:{writing}\:{the}\:{size}\:{of}\: \\ $$$${a}\:{rectangle}\:{in}\:{the}\:{form}\:{of}\: \\ $$$${length}\:×\:{width}\:?\:{mean}\:{if}\:{you} \\ $$$${write}\:{a}\:{rectangle}\:{with}\:{the}\:{size} \\ $$$${of}\:\mathrm{2}{m}\:×\:\mathrm{4}{m}\:,\:{then}\:{the}\:{length} \\ $$$${is}\:\mathrm{2}{m}?\: \\ $$
Commented by MJS last updated on 20/Apr/20

$$\mathrm{in}\:\mathrm{Austria}\:\mathrm{we}'\mathrm{re}\:\mathrm{speaking}\:\mathrm{German}.\:\mathrm{here}, \\ $$$$\mathrm{length}\:\mathrm{is}\:“\mathrm{l}\overset{..} {\mathrm{a}nge}''\:\mathrm{and}\:\mathrm{width}\:\mathrm{is}\:“\mathrm{breite}''\:\mathrm{not} \\ $$$$“\mathrm{weite}''\:\mathrm{which}\:\mathrm{is}\:\mathrm{only}\:\mathrm{used}\:\mathrm{for}\:\mathrm{openings}. \\ $$$$\mathrm{so}\:\mathrm{for}\:\mathrm{me}\:\mathrm{it}\:\mathrm{was}\:\mathrm{clear}\:\mathrm{that}\:\mathrm{a}\:\mathrm{table}\:\mathrm{is}\:\mathrm{longer} \\ $$$$\mathrm{than}\:\mathrm{it}\:\mathrm{is}\:\mathrm{broad}.\:\mathrm{calculate}\:\mathrm{what}\:\mathrm{you}\:\mathrm{want}, \\ $$$$\mathrm{the}\:\mathrm{path}\:\mathrm{is}\:\mathrm{there}. \\ $$
