Question Number 89977 by I want to learn more last updated on 20/Apr/20
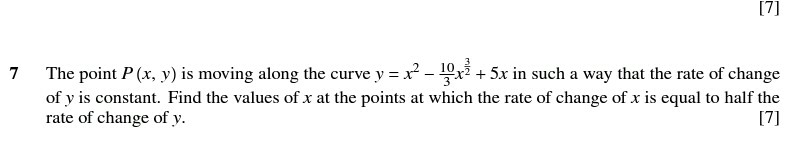
Commented by jagoll last updated on 20/Apr/20
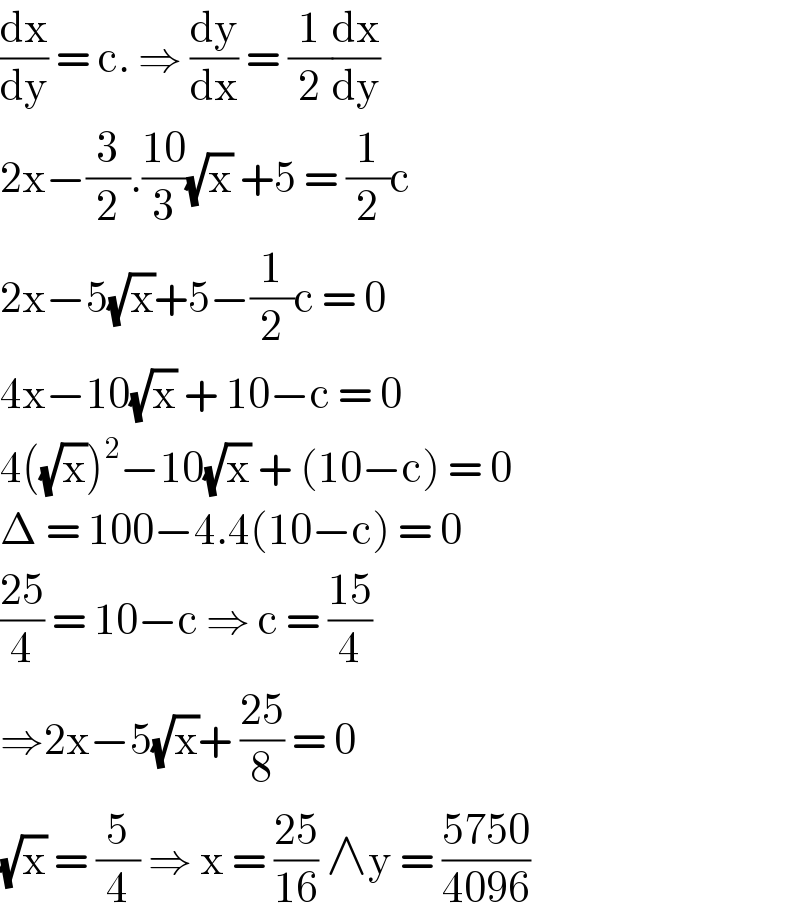
$$\frac{\mathrm{dx}}{\mathrm{dy}}\:=\:\mathrm{c}.\:\Rightarrow\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\frac{\mathrm{dx}}{\mathrm{dy}} \\ $$$$\mathrm{2x}−\frac{\mathrm{3}}{\mathrm{2}}.\frac{\mathrm{10}}{\mathrm{3}}\sqrt{\mathrm{x}}\:+\mathrm{5}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{c} \\ $$$$\mathrm{2x}−\mathrm{5}\sqrt{\mathrm{x}}+\mathrm{5}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{c}\:=\:\mathrm{0} \\ $$$$\mathrm{4x}−\mathrm{10}\sqrt{\mathrm{x}}\:+\:\mathrm{10}−\mathrm{c}\:=\:\mathrm{0} \\ $$$$\mathrm{4}\left(\sqrt{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{10}\sqrt{\mathrm{x}}\:+\:\left(\mathrm{10}−\mathrm{c}\right)\:=\:\mathrm{0} \\ $$$$\Delta\:=\:\mathrm{100}−\mathrm{4}.\mathrm{4}\left(\mathrm{10}−\mathrm{c}\right)\:=\:\mathrm{0}\: \\ $$$$\frac{\mathrm{25}}{\mathrm{4}}\:=\:\mathrm{10}−\mathrm{c}\:\Rightarrow\:\mathrm{c}\:=\:\frac{\mathrm{15}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{2x}−\mathrm{5}\sqrt{\mathrm{x}}+\:\frac{\mathrm{25}}{\mathrm{8}}\:=\:\mathrm{0} \\ $$$$\sqrt{\mathrm{x}}\:=\:\frac{\mathrm{5}}{\mathrm{4}}\:\Rightarrow\:\mathrm{x}\:=\:\frac{\mathrm{25}}{\mathrm{16}}\:\wedge\mathrm{y}\:=\:\frac{\mathrm{5750}}{\mathrm{4096}} \\ $$
Commented by I want to learn more last updated on 20/Apr/20

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
