Question Number 89980 by swizanjere@gmail.com last updated on 20/Apr/20

Commented by john santu last updated on 20/Apr/20
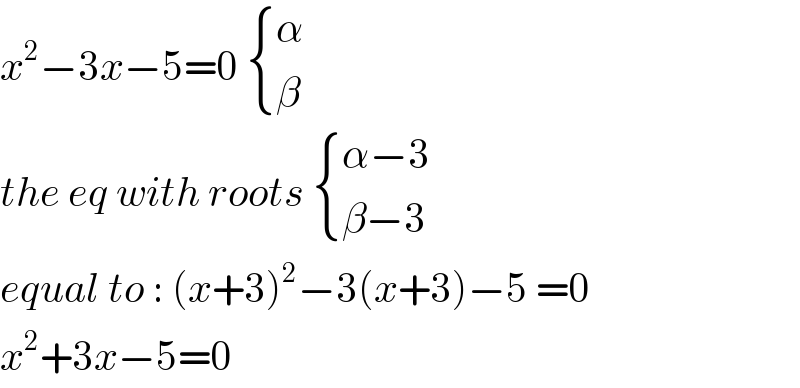
$${x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{5}=\mathrm{0}\:\begin{cases}{\alpha}\\{\beta}\end{cases} \\ $$$${the}\:{eq}\:{with}\:{roots}\:\begin{cases}{\alpha−\mathrm{3}}\\{\beta−\mathrm{3}}\end{cases} \\ $$$${equal}\:{to}\::\:\left({x}+\mathrm{3}\right)^{\mathrm{2}} −\mathrm{3}\left({x}+\mathrm{3}\right)−\mathrm{5}\:=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{5}=\mathrm{0} \\ $$
Commented by john santu last updated on 20/Apr/20
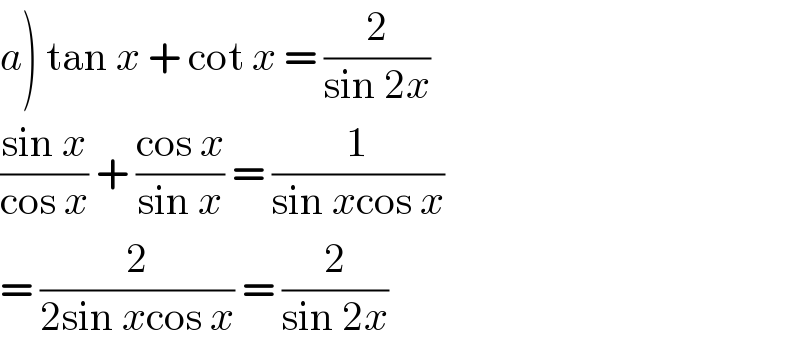
$$\left.{a}\right)\:\mathrm{tan}\:{x}\:+\:\mathrm{cot}\:{x}\:=\:\frac{\mathrm{2}}{\mathrm{sin}\:\mathrm{2}{x}} \\ $$$$\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}\:+\:\frac{\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}}\:=\:\frac{\mathrm{1}}{\mathrm{sin}\:{x}\mathrm{cos}\:{x}} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{2sin}\:{x}\mathrm{cos}\:{x}}\:=\:\frac{\mathrm{2}}{\mathrm{sin}\:\mathrm{2}{x}} \\ $$
