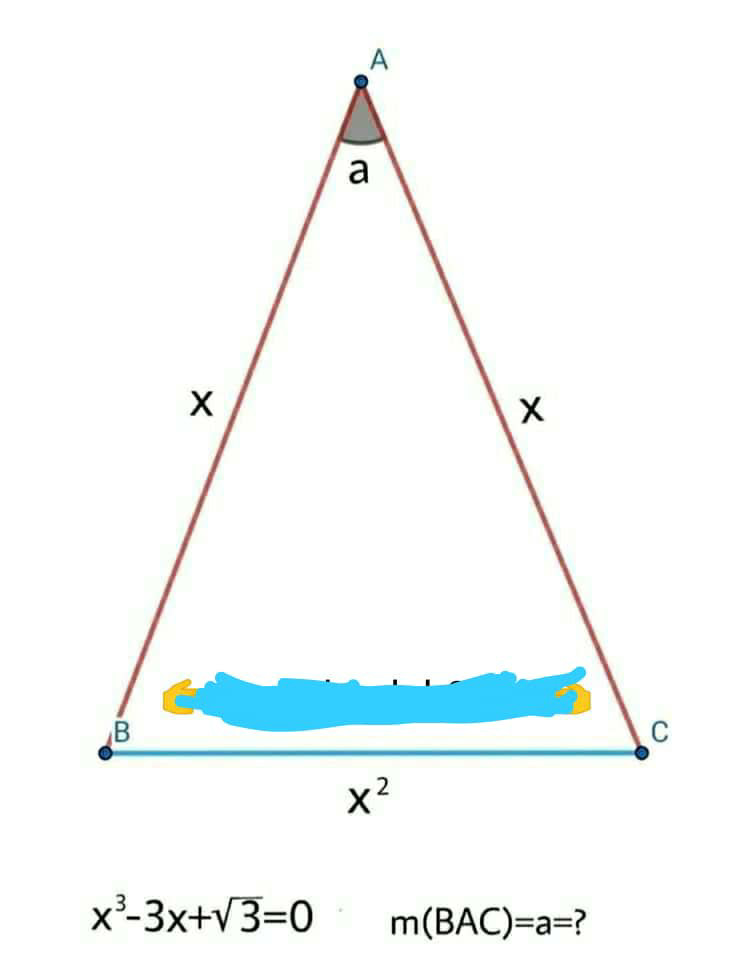
Question Number 90011 by I want to learn more last updated on 20/Apr/20
Commented by mr W last updated on 21/Apr/20
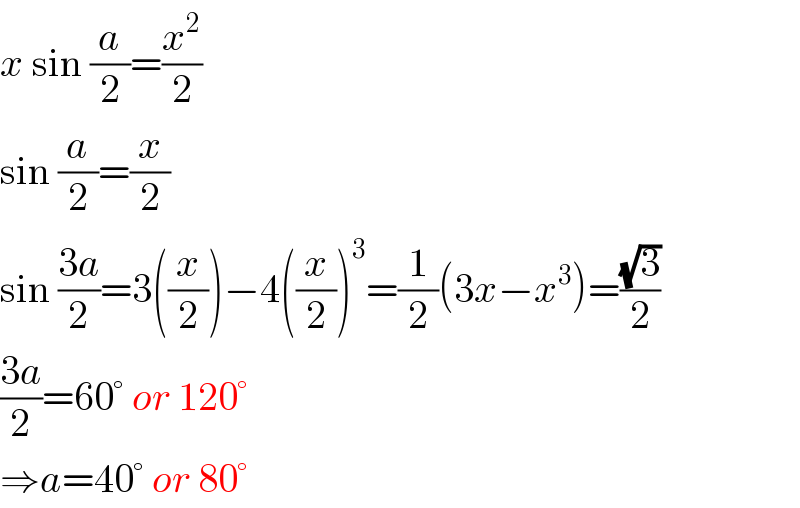
$${x}\:\mathrm{sin}\:\frac{{a}}{\mathrm{2}}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{sin}\:\frac{{a}}{\mathrm{2}}=\frac{{x}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\frac{\mathrm{3}{a}}{\mathrm{2}}=\mathrm{3}\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{4}\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}{x}−{x}^{\mathrm{3}} \right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\frac{\mathrm{3}{a}}{\mathrm{2}}=\mathrm{60}°\:{or}\:\mathrm{120}° \\ $$$$\Rightarrow{a}=\mathrm{40}°\:{or}\:\mathrm{80}° \\ $$
Commented by I want to learn more last updated on 20/Apr/20
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Commented by MJS last updated on 21/Apr/20
![is a=80° also possible? x^3 −3x+(√3)=0 x_1 =2sin (π/9) ⇒ a=40° x_2 =2sin ((2π)/9) ⇒ a=80° x_3 =−2cos (π/(18)) [impossible]](https://www.tinkutara.com/question/Q90045.png)
$$\mathrm{is}\:{a}=\mathrm{80}°\:\mathrm{also}\:\mathrm{possible}? \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{x}+\sqrt{\mathrm{3}}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{2sin}\:\frac{\pi}{\mathrm{9}}\:\Rightarrow\:{a}=\mathrm{40}° \\ $$$${x}_{\mathrm{2}} =\mathrm{2sin}\:\frac{\mathrm{2}\pi}{\mathrm{9}}\:\Rightarrow\:{a}=\mathrm{80}° \\ $$$${x}_{\mathrm{3}} =−\mathrm{2cos}\:\frac{\pi}{\mathrm{18}}\:\left[\mathrm{impossible}\right] \\ $$
Commented by john santu last updated on 21/Apr/20
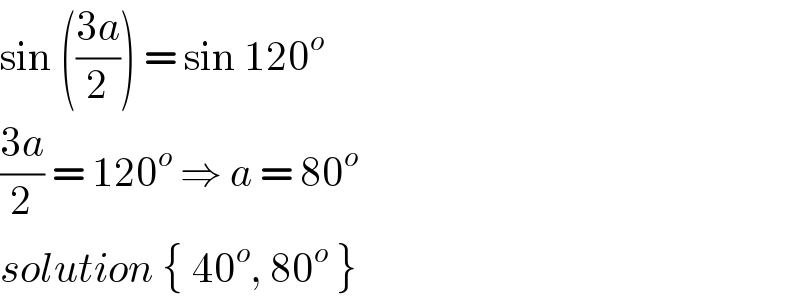
$$\mathrm{sin}\:\left(\frac{\mathrm{3}{a}}{\mathrm{2}}\right)\:=\:\mathrm{sin}\:\mathrm{120}^{{o}} \\ $$$$\frac{\mathrm{3}{a}}{\mathrm{2}}\:=\:\mathrm{120}^{{o}} \:\Rightarrow\:{a}\:=\:\mathrm{80}^{{o}} \\ $$$${solution}\:\left\{\:\mathrm{40}^{{o}} ,\:\mathrm{80}^{{o}} \:\right\} \\ $$
Commented by mr W last updated on 21/Apr/20

$${yes}. \\ $$
Commented by I want to learn more last updated on 21/Apr/20

$$\mathrm{Thanks}\:\mathrm{sirs} \\ $$
