Question Number 90058 by mr W last updated on 21/Apr/20
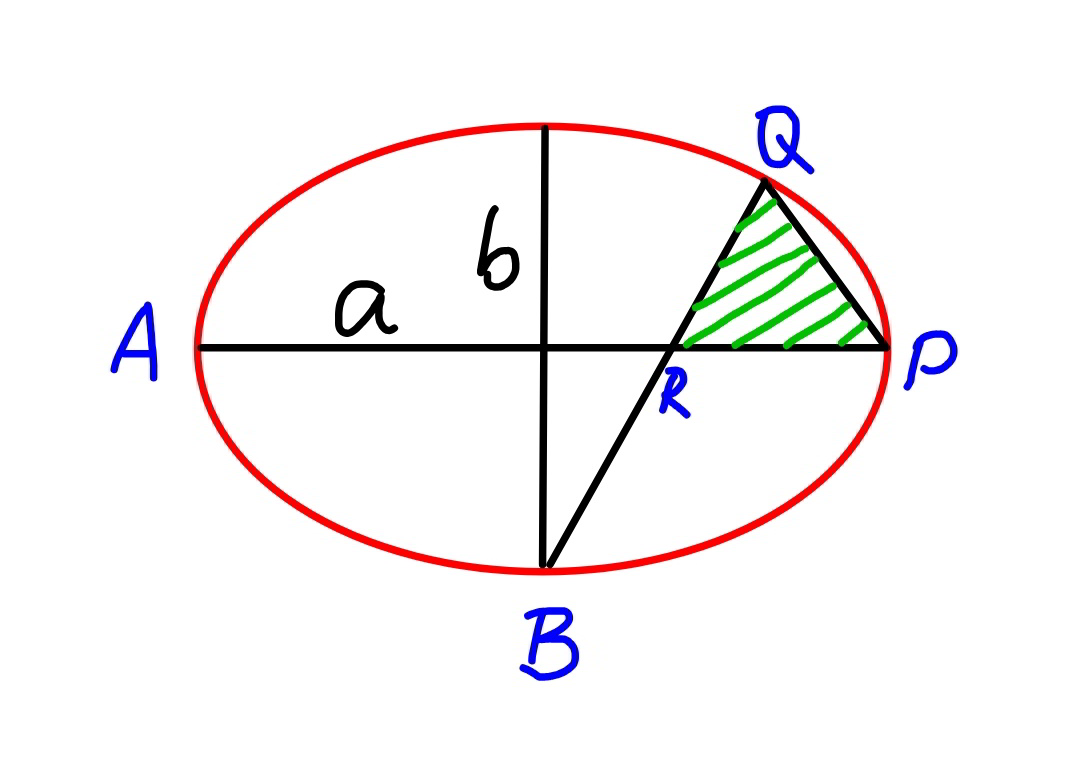
Commented by mr W last updated on 21/Apr/20
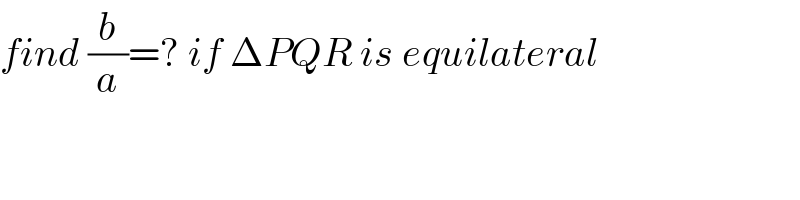
$${find}\:\frac{{b}}{{a}}=?\:{if}\:\Delta{PQR}\:{is}\:{equilateral} \\ $$
Answered by ajfour last updated on 21/Apr/20
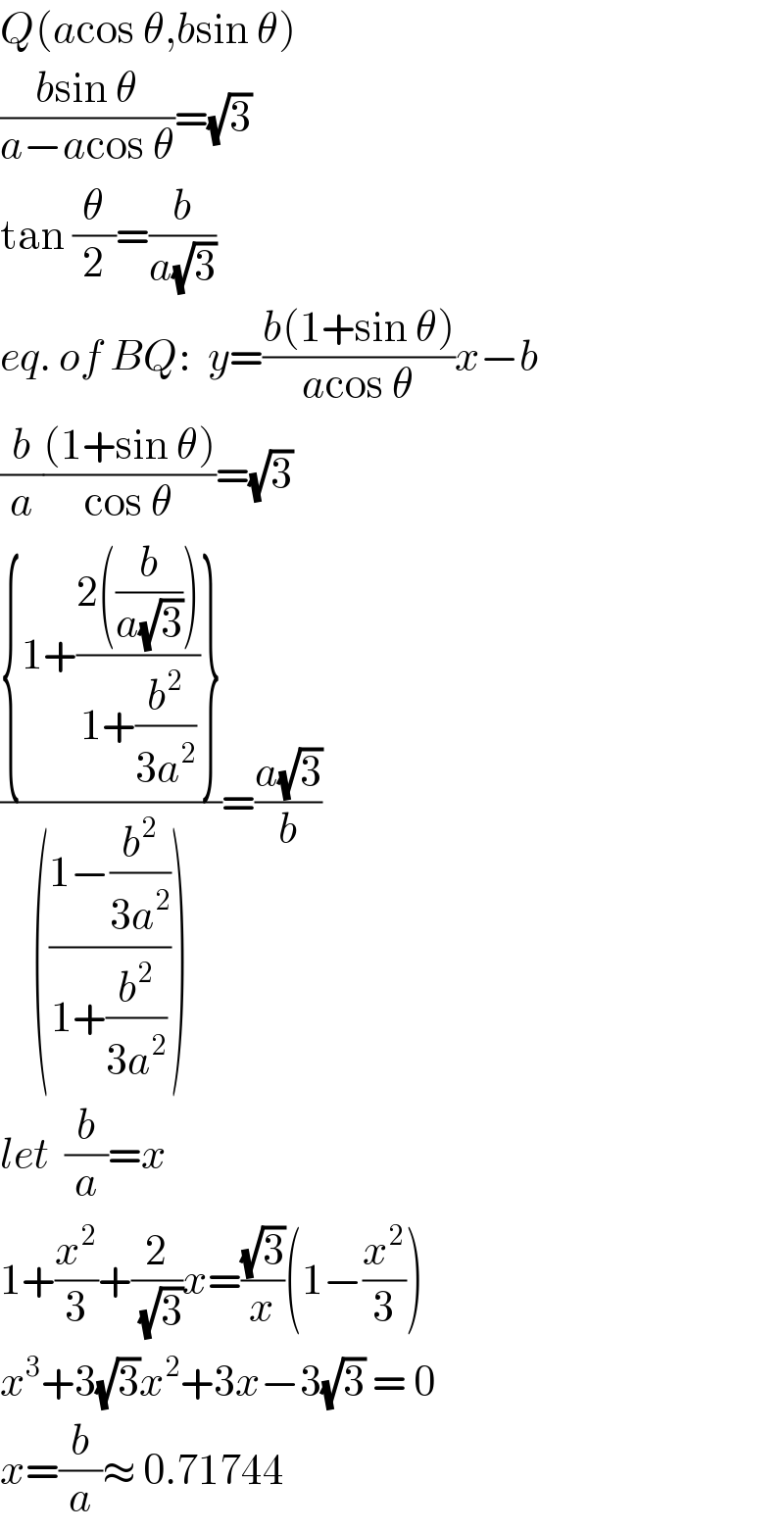
$${Q}\left({a}\mathrm{cos}\:\theta,{b}\mathrm{sin}\:\theta\right) \\ $$$$\frac{{b}\mathrm{sin}\:\theta}{{a}−{a}\mathrm{cos}\:\theta}=\sqrt{\mathrm{3}} \\ $$$$\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{{b}}{{a}\sqrt{\mathrm{3}}} \\ $$$${eq}.\:{of}\:{BQ}:\:\:{y}=\frac{{b}\left(\mathrm{1}+\mathrm{sin}\:\theta\right)}{{a}\mathrm{cos}\:\theta}{x}−{b} \\ $$$$\frac{{b}}{{a}}\frac{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)}{\mathrm{cos}\:\theta}=\sqrt{\mathrm{3}} \\ $$$$\frac{\left\{\mathrm{1}+\frac{\mathrm{2}\left(\frac{{b}}{{a}\sqrt{\mathrm{3}}}\right)}{\mathrm{1}+\frac{{b}^{\mathrm{2}} }{\mathrm{3}{a}^{\mathrm{2}} }}\right\}}{\left(\frac{\mathrm{1}−\frac{{b}^{\mathrm{2}} }{\mathrm{3}{a}^{\mathrm{2}} }}{\mathrm{1}+\frac{{b}^{\mathrm{2}} }{\mathrm{3}{a}^{\mathrm{2}} }}\right)}=\frac{{a}\sqrt{\mathrm{3}}}{{b}} \\ $$$${let}\:\:\frac{{b}}{{a}}={x} \\ $$$$\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{x}=\frac{\sqrt{\mathrm{3}}}{{x}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{3}}\right) \\ $$$${x}^{\mathrm{3}} +\mathrm{3}\sqrt{\mathrm{3}}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{3}\sqrt{\mathrm{3}}\:=\:\mathrm{0} \\ $$$${x}=\frac{{b}}{{a}}\approx\:\mathrm{0}.\mathrm{71744} \\ $$
Commented by mr W last updated on 21/Apr/20

$${thanks}\:{sir}! \\ $$
Commented by peter frank last updated on 21/Apr/20
$${help}\:{Qn}\:\:\mathrm{90030} \\ $$
