Question Number 90086 by I want to learn more last updated on 21/Apr/20

Commented by I want to learn more last updated on 21/Apr/20

$$\mathrm{Ohh},\:\:\mathrm{i}\:\mathrm{grab} \\ $$
Commented by I want to learn more last updated on 21/Apr/20
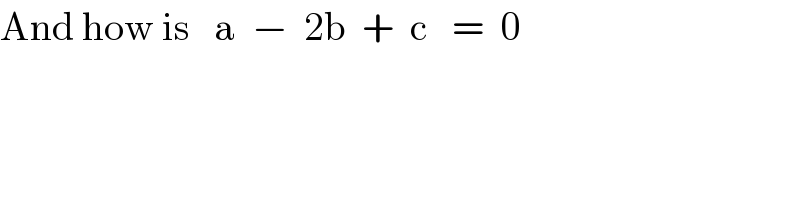
$$\mathrm{And}\:\mathrm{how}\:\mathrm{is}\:\:\:\mathrm{a}\:\:−\:\:\mathrm{2b}\:\:+\:\:\mathrm{c}\:\:\:=\:\:\mathrm{0} \\ $$
Commented by mr W last updated on 21/Apr/20
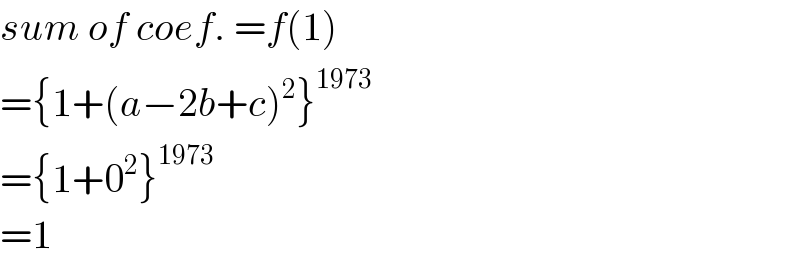
$${sum}\:{of}\:{coef}.\:={f}\left(\mathrm{1}\right) \\ $$$$=\left\{\mathrm{1}+\left({a}−\mathrm{2}{b}+{c}\right)^{\mathrm{2}} \right\}^{\mathrm{1973}} \\ $$$$=\left\{\mathrm{1}+\mathrm{0}^{\mathrm{2}} \right\}^{\mathrm{1973}} \\ $$$$=\mathrm{1} \\ $$
Commented by I want to learn more last updated on 21/Apr/20

$$\mathrm{Sir}\:\mathrm{why}\:\mathrm{is}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{coefficient}\:\:=\:\:\mathrm{1} \\ $$
Commented by john santu last updated on 21/Apr/20
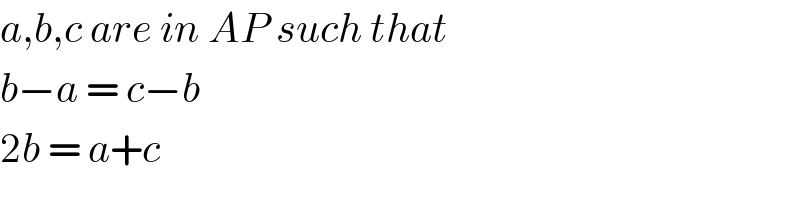
$${a},{b},{c}\:{are}\:{in}\:{AP}\:{such}\:{that}\: \\ $$$${b}−{a}\:=\:{c}−{b}\: \\ $$$$\mathrm{2}{b}\:=\:{a}+{c}\: \\ $$
Commented by mr W last updated on 21/Apr/20
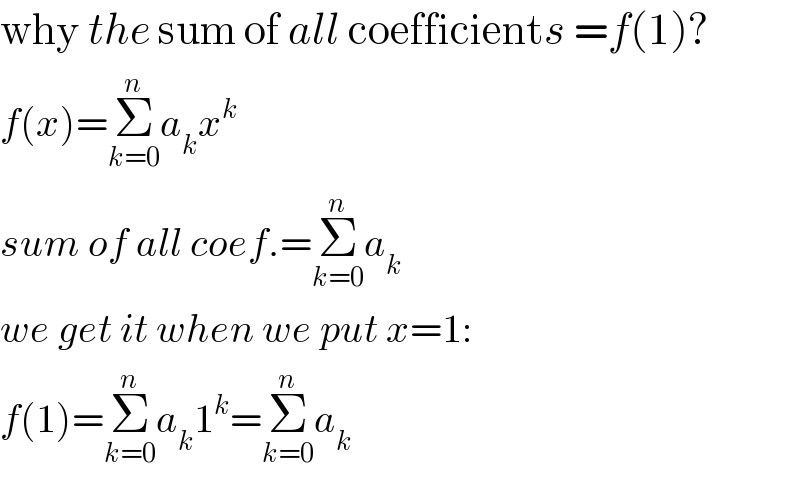
$$\mathrm{why}\:{the}\:\mathrm{sum}\:\mathrm{of}\:{all}\:\mathrm{coefficient}{s}\:={f}\left(\mathrm{1}\right)? \\ $$$${f}\left({x}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{k}} {x}^{{k}} \\ $$$${sum}\:{of}\:{all}\:{coef}.=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{k}} \\ $$$${we}\:{get}\:{it}\:{when}\:{we}\:{put}\:{x}=\mathrm{1}: \\ $$$${f}\left(\mathrm{1}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{k}} \mathrm{1}^{{k}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{k}} \\ $$
Commented by I want to learn more last updated on 21/Apr/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
