Question Number 90326 by ajfour last updated on 22/Apr/20

Commented by ajfour last updated on 22/Apr/20
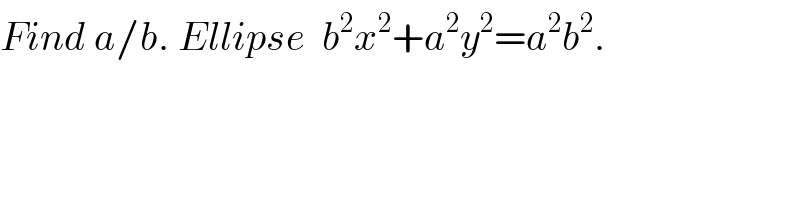
$${Find}\:{a}/{b}.\:{Ellipse}\:\:{b}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} {y}^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} . \\ $$
Answered by ajfour last updated on 22/Apr/20
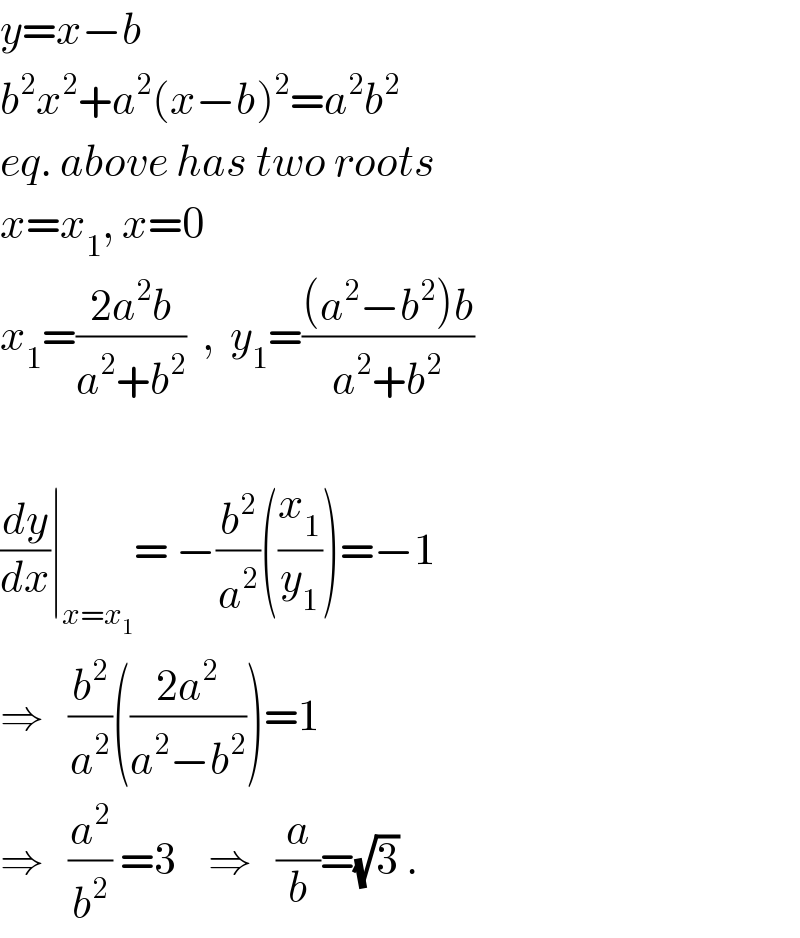
$${y}={x}−{b} \\ $$$${b}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} \left({x}−{b}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$${eq}.\:{above}\:{has}\:{two}\:{roots} \\ $$$${x}={x}_{\mathrm{1}} ,\:{x}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{2}{a}^{\mathrm{2}} {b}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\:,\:\:{y}_{\mathrm{1}} =\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){b}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$ \\ $$$$\frac{{dy}}{{dx}}\mid_{{x}={x}_{\mathrm{1}} } =\:−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\left(\frac{{x}_{\mathrm{1}} }{{y}_{\mathrm{1}} }\right)=−\mathrm{1} \\ $$$$\Rightarrow\:\:\:\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\left(\frac{\mathrm{2}{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)=\mathrm{1} \\ $$$$\Rightarrow\:\:\:\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:=\mathrm{3}\:\:\:\:\Rightarrow\:\:\:\frac{{a}}{{b}}=\sqrt{\mathrm{3}}\:. \\ $$
Commented by ajfour last updated on 22/Apr/20
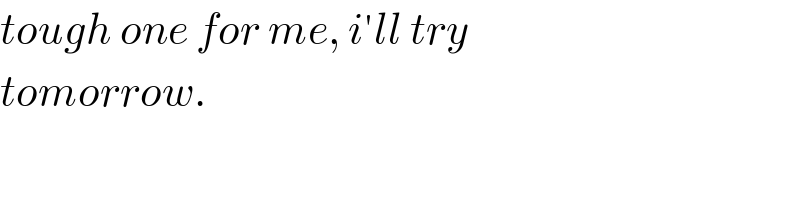
$${tough}\:{one}\:{for}\:{me},\:{i}'{ll}\:{try} \\ $$$${tomorrow}. \\ $$
