Question Number 90331 by ajfour last updated on 22/Apr/20
Commented by ajfour last updated on 22/Apr/20
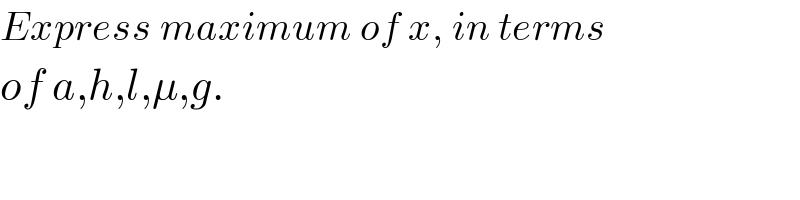
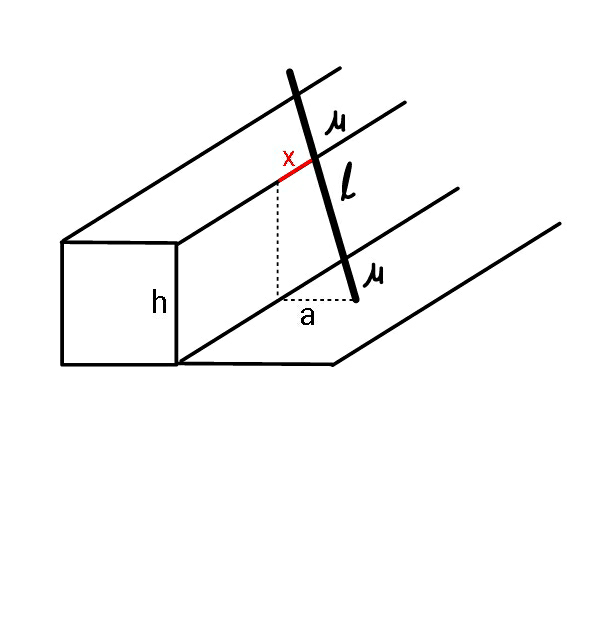
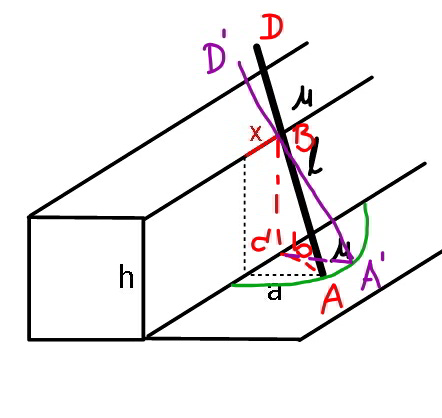
$${Express}\:{maximum}\:{of}\:{x},\:{in}\:{terms} \\ $$$${of}\:{a},{h},{l},\mu,{g}. \\ $$
Answered by mr W last updated on 25/Apr/20
Commented by mr W last updated on 26/Apr/20
![the stick is in equilibrium under the acting of three forces, therefore these three must be in the same plane and they must meet at the same point. φ=tan^(−1) μ tan θ=(h/( (√(a^2 +x^2 )))) α=φ β=θ−φ ((SM)/(sin ((π/2)−θ−φ)))=((AM)/(sin φ)) ⇒SM=((cos (θ+φ) l)/(2 sin φ))=(l/2)(((cos θ)/μ)−sin θ) ((MB)/(sin β))=((SM)/(sin ((π/2)−θ+β))) ⇒MB=((sin (θ−φ))/(cos φ))(((cos θ)/μ)−sin θ)×(l/2) ⇒MB=(((cos θ−μ sin θ)(sin θ−μ cos θ))/μ)×(l/2) AB=(h/(sin θ)) [1+(((cos θ−μ sin θ)(sin θ−μ cos θ))/μ)]×(l/2)=(h/(sin θ)) sin θ[1+(((cos θ−μ sin θ)(sin θ−μ cos θ))/μ)]=((2h)/l) ⇒sin^2 θ cos θ=((2μh)/((1+μ^2 )l)) with λ=((μh)/((1+μ^2 )l)) ⇒cos^3 θ−cos θ+2λ=0 cos θ=((2(√3))/3) sin ((1/3)sin^(−1) 3(√3)λ+((2kπ)/3)) (k=0,1,2) generally we get two suitable values for θ. the smaller one leads to larger value of x, therefore we take only this solution: let (1/δ)=((2(√3))/3) sin [(1/3)sin^(−1) ((3(√3)μh)/((1+μ^2 )l))+((2π)/3)] tan^2 θ=(h^2 /(a^2 +x^2 ))=(1/(cos^2 θ))−1=δ^2 −1 ⇒x^2 =(h^2 /(δ^2 −1))−a^2 ⇒x=(√((h^2 /(δ^2 −1))−a^2 ))](https://www.tinkutara.com/question/Q90675.png)
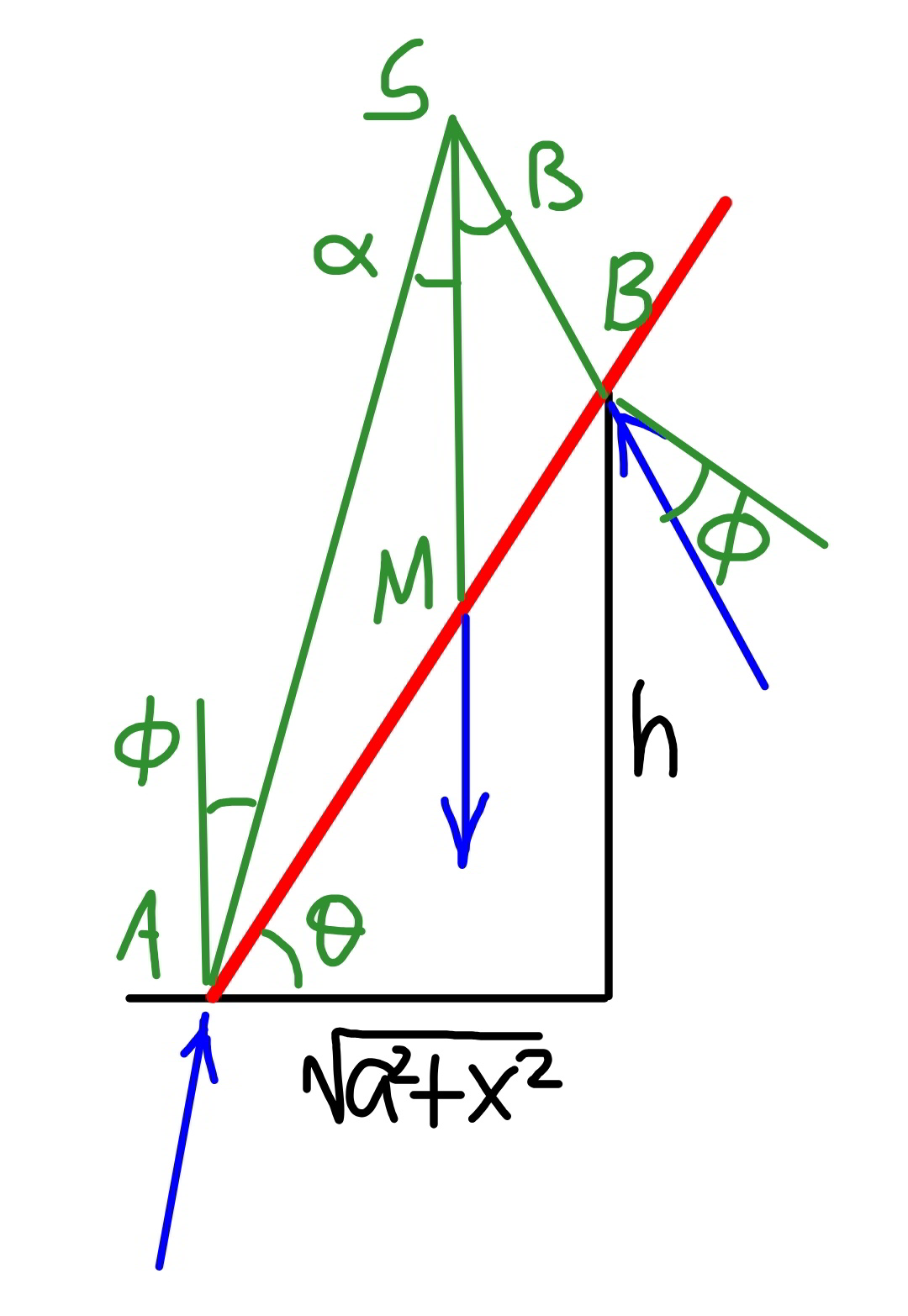
$${the}\:{stick}\:{is}\:{in}\:{equilibrium}\:{under}\:{the} \\ $$$${acting}\:{of}\:{three}\:{forces},\:{therefore} \\ $$$${these}\:{three}\:{must}\:{be}\:{in}\:{the}\:{same}\:{plane} \\ $$$${and}\:{they}\:{must}\:{meet}\:{at}\:{the}\:{same}\:{point}. \\ $$$$\phi=\mathrm{tan}^{−\mathrm{1}} \mu \\ $$$$\mathrm{tan}\:\theta=\frac{{h}}{\:\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }} \\ $$$$\alpha=\phi \\ $$$$\beta=\theta−\phi \\ $$$$\frac{{SM}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\theta−\phi\right)}=\frac{{AM}}{\mathrm{sin}\:\phi} \\ $$$$\Rightarrow{SM}=\frac{\mathrm{cos}\:\left(\theta+\phi\right)\:{l}}{\mathrm{2}\:\mathrm{sin}\:\phi}=\frac{{l}}{\mathrm{2}}\left(\frac{\mathrm{cos}\:\theta}{\mu}−\mathrm{sin}\:\theta\right) \\ $$$$\frac{{MB}}{\mathrm{sin}\:\beta}=\frac{{SM}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\theta+\beta\right)} \\ $$$$\Rightarrow{MB}=\frac{\mathrm{sin}\:\left(\theta−\phi\right)}{\mathrm{cos}\:\phi}\left(\frac{\mathrm{cos}\:\theta}{\mu}−\mathrm{sin}\:\theta\right)×\frac{{l}}{\mathrm{2}} \\ $$$$\Rightarrow{MB}=\frac{\left(\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta\right)\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right)}{\mu}×\frac{{l}}{\mathrm{2}} \\ $$$${AB}=\frac{{h}}{\mathrm{sin}\:\theta} \\ $$$$\left[\mathrm{1}+\frac{\left(\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta\right)\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right)}{\mu}\right]×\frac{{l}}{\mathrm{2}}=\frac{{h}}{\mathrm{sin}\:\theta} \\ $$$$\mathrm{sin}\:\theta\left[\mathrm{1}+\frac{\left(\mathrm{cos}\:\theta−\mu\:\mathrm{sin}\:\theta\right)\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right)}{\mu}\right]=\frac{\mathrm{2}{h}}{{l}} \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{2}} \:\theta\:\mathrm{cos}\:\theta=\frac{\mathrm{2}\mu{h}}{\left(\mathrm{1}+\mu^{\mathrm{2}} \right){l}} \\ $$$${with}\:\lambda=\frac{\mu{h}}{\left(\mathrm{1}+\mu^{\mathrm{2}} \right){l}} \\ $$$$\Rightarrow\mathrm{cos}^{\mathrm{3}} \:\theta−\mathrm{cos}\:\theta+\mathrm{2}\lambda=\mathrm{0} \\ $$$$\mathrm{cos}\:\theta=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \mathrm{3}\sqrt{\mathrm{3}}\lambda+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right)\:\left({k}=\mathrm{0},\mathrm{1},\mathrm{2}\right) \\ $$$${generally}\:{we}\:{get}\:{two}\:{suitable}\:{values} \\ $$$${for}\:\theta.\:{the}\:{smaller}\:{one}\:{leads}\:{to}\:{larger} \\ $$$${value}\:{of}\:{x},\:{therefore}\:{we}\:{take}\:{only} \\ $$$${this}\:{solution}: \\ $$$${let}\:\frac{\mathrm{1}}{\delta}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\:\mathrm{sin}\:\left[\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}\mu{h}}{\left(\mathrm{1}+\mu^{\mathrm{2}} \right){l}}+\frac{\mathrm{2}\pi}{\mathrm{3}}\right] \\ $$$$\mathrm{tan}^{\mathrm{2}} \:\theta=\frac{{h}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\theta}−\mathrm{1}=\delta^{\mathrm{2}} −\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\frac{{h}^{\mathrm{2}} }{\delta^{\mathrm{2}} −\mathrm{1}}−{a}^{\mathrm{2}} \\ $$$$\Rightarrow{x}=\sqrt{\frac{{h}^{\mathrm{2}} }{\delta^{\mathrm{2}} −\mathrm{1}}−{a}^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 26/Apr/20

$${great}\:{way}\:{sir}! \\ $$$${but}\:{two}\:{things} \\ $$$${a}\:{little}\:{typo}\:{of}\:{no}\:{consequence} \\ $$$$\:\:\mathrm{cos}\:^{\mathrm{3}} \theta−\mathrm{cos}\:^{\mathrm{2}} \theta+\mathrm{2}\lambda=\mathrm{0} \\ $$$${And}\:{what}\:{if}\:{ground}\:{point}\:{of} \\ $$$${rod},\:{is}\:{not}\:{about}\:{to}\:{slide},\:{but} \\ $$$${just}\:{the}\:{point}\:{resting}\:{on}\:{the}\: \\ $$$${edge}\:{is}\:{about}\:{to}\:{slide},\:{then} \\ $$$${x}_{{max}} \:{shall}\:{be}\:{greater}\:{or}\:{smaller} \\ $$$${than}\:{the}\:{already}\:{found}\:{result}? \\ $$
Commented by mr W last updated on 25/Apr/20

Commented by ajfour last updated on 26/Apr/20
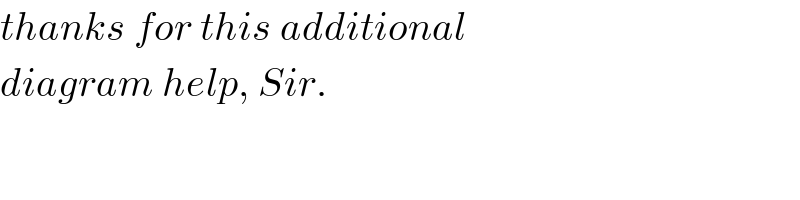
$${thanks}\:{for}\:{this}\:{additional} \\ $$$${diagram}\:{help},\:{Sir}.\: \\ $$
Commented by mr W last updated on 26/Apr/20

$${if}\:{the}\:{point}\:{on}\:{groud}\:{is}\:{not}\:{about}\:{to} \\ $$$${slide},\:{then}\:\phi\:{is}\:{smaller}\:{than}\:{now}\: \\ $$$$\left(\mathrm{tan}^{−\mathrm{1}} \mu\right),\:{that}\:{means}\:{the}\:{stick}\:{is} \\ $$$${steeper}\:{and}\:{x}\:{is}\:{smaller}. \\ $$
Commented by mr W last updated on 26/Apr/20
Commented by mr W last updated on 26/Apr/20

$${but}\:{to}\:{be}\:{honest},\:{i}\:{am}\:{uncertain}\:{if}\:{my} \\ $$$${solution}\:{is}\:{correct}.\:{let}\:{b}=\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$${my}\:{solution}\:{says}\:{the}\:{foot}\:{the}\:{stick} \\ $$$${can}\:{stay}\:{at}\:{any}\:{point}\:{on}\:{the}\:{green} \\ $$$${semicircle}\:{with}\:{radius}\:{b}.\:{but}\:{this} \\ $$$${can}\:{not}\:{be}\:{true}.\:{at}\:{the}\:{position}\:{A}'{D}' \\ $$$${the}\:{stick}\:{obtains}\:{no}\:{friction}\:{along} \\ $$$${the}\:{edge},\:{i}\:{think}\:{for}\:{the}\:{case}\:{the} \\ $$$${solution}\:{is}\:{correct}.\:{but}\:{at}\:{any}\:{other} \\ $$$${position}\:{the}\:{stick}\:{can}\:{slide}\:{along}\:{the} \\ $$$${edge},\:{this}\:{friction}\:{plays}\:{a}\:{role}.\:{but} \\ $$$${this}\:{is}\:{not}\:{considered}\:{in}\:{my}\:{solution}, \\ $$$${because}\:{i}\:{don}'{t}\:{know}\:{how}\:{to}\:{treat}. \\ $$
Commented by mr W last updated on 26/Apr/20

$${i}\:{hope}\:{you}\:{can}\:{bring}\:{some}\:{light}\:{into} \\ $$$${this}\:{point}:\:{how}\:{is}\:{the}\:{contact}\:{force} \\ $$$${and}\:{friction}\:{force}\:{between}\:{the}\:{stick} \\ $$$${and}\:{the}\:{edge}\:{if}\:{the}\:{strick}\:{is}\:{not}\:{at} \\ $$$${the}\:{position}\:{A}'{D}'. \\ $$
Commented by ajfour last updated on 26/Apr/20

$${normal}\:{reaction}\:\bot\:{to}\:{stick}, \\ $$$${friction}\:{along}\:{the}\:{edge},\:{sideways} \\ $$$${to}\:{the}\:{length}\:{of}\:{stick},\:{and} \\ $$$${along}\:{the}\:{length}\:{of}\:{stick}\:{as}\:{well}. \\ $$$${why}\:{not}\:{consider}\:{the}\:{stick}\:{to}\:{be} \\ $$$${hinged}\:{at}\:{the}\:{bottom}\:\left({but}\:{allowed}\right. \\ $$$$\left.{to}\:{incline}\:{any}\:{way}\right)\:{and}\:{then} \\ $$$${solve}\:{the}\:{problem},\:{Sir}? \\ $$$${i}\:{shall}\:{try}\:{once}.. \\ $$
Commented by ajfour last updated on 26/Apr/20

$${i}\:{had}\:{happened}\:{to}\:{throw}\:{a}\:{fallen} \\ $$$${matchstick}\:\mathrm{3}-\mathrm{4}\:{dsys}\:{back}\:,\left({when}\right. \\ $$$${i}\:{was}\:{thinking}\:{of}\:{creating}\:{a} \\ $$$$\left.{new}\:{physics}\:{question}\right) \\ $$$${randomly}\:{on}\:{the}\:{table},\:{over}\: \\ $$$${which}\:{were}\:{lying}\:{two}\:{books} \\ $$$${larger}\:{below}\:{and}\:{smaller}\:{above}, \\ $$$${the}\:{matchstick}\:{happened}\:{to} \\ $$$${rest}\:{like}\:{in}\:{the}\:{question},\:{thus} \\ $$$${nature}\:{itself}\:{answered}\:{my}\:{wish}. \\ $$$$\left({thought}\:{of}\:{sharing}\:{this}\:{even},\right. \\ $$$$\:\:{with}\:{you}\:{Sir},\:{hidden}\: \\ $$$$\left.{communications}\right). \\ $$
Commented by mr W last updated on 26/Apr/20

$${i}\:{made}\:{an}\:{experiment}\:{on}\:{our}\:{dinner} \\ $$$${table}\:{and}\:{realised}\:{that}\:{my}\:{solution} \\ $$$${is}\:{not}\:{correct}.\:{i}'{ll}\:{continue}\:{to}\:{think} \\ $$$${about}\:{it}. \\ $$
