Menu Close

Question-90347

Tinku Tara 0 Comments
Pin




Question Number 90347 by mr W last updated on 22/Apr/20
Commented by mr W last updated on 22/Apr/20
the parabola has the same shape as y=x^2 . find it′s equation if it passes through O, A, B as shown. [for some reason ajfour sir has deleted this question. but it is a good question.]
$${the}\:{parabola}\:{has}\:{the}\:{same}\:{shape}\:{as} \\ $$$${y}={x}^{\mathrm{2}} .\:{find}\:{it}'{s}\:{equation}\:{if}\:{it}\:{passes} \\ $$$${through}\:{O},\:{A},\:{B}\:{as}\:{shown}. \\ $$$$ \\ $$$$\left[{for}\:{some}\:{reason}\:{ajfour}\:{sir}\:{has}\:{deleted}\right. \\ $$$$\left.{this}\:{question}.\:{but}\:{it}\:{is}\:{a}\:{good}\:{question}.\right] \\ $$
Commented by MJS last updated on 23/Apr/20
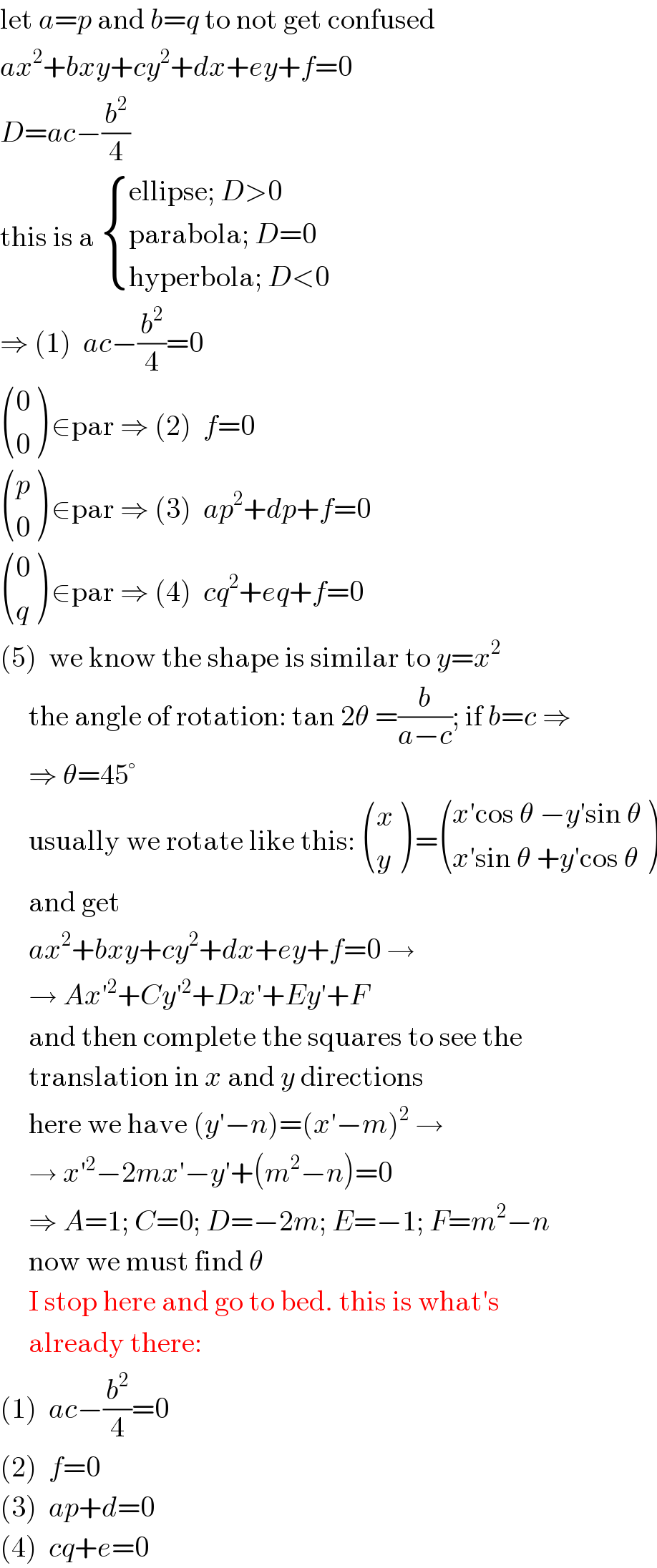
let a=p and b=q to not get confused ax^2 +bxy+cy^2 +dx+ey+f=0 D=ac−(b^2 /4) this is a { ((ellipse; D>0)),((parabola; D=0)),((hyperbola; D<0)) :} ⇒ (1) ac−(b^2 /4)=0 ((0),(0) ) ∈par ⇒ (2) f=0 ((p),(0) ) ∈par ⇒ (3) ap^2 +dp+f=0 ((0),(q) ) ∈par ⇒ (4) cq^2 +eq+f=0 (5) we know the shape is similar to y=x^2 the angle of rotation: tan 2θ =(b/(a−c)); if b=c ⇒ ⇒ θ=45° usually we rotate like this: ((x),(y) ) = (((x′cos θ −y′sin θ)),((x′sin θ +y′cos θ)) ) and get ax^2 +bxy+cy^2 +dx+ey+f=0 → → Ax′^2 +Cy′^2 +Dx′+Ey′+F and then complete the squares to see the translation in x and y directions here we have (y′−n)=(x′−m)^2 → → x′^2 −2mx′−y′+(m^2 −n)=0 ⇒ A=1; C=0; D=−2m; E=−1; F=m^2 −n now we must find θ I stop here and go to bed. this is what′s already there: (1) ac−(b^2 /4)=0 (2) f=0 (3) ap+d=0 (4) cq+e=0
$$\mathrm{let}\:{a}={p}\:\mathrm{and}\:{b}={q}\:\mathrm{to}\:\mathrm{not}\:\mathrm{get}\:\mathrm{confused} \\ $$$${ax}^{\mathrm{2}} +{bxy}+{cy}^{\mathrm{2}} +{dx}+{ey}+{f}=\mathrm{0} \\ $$$${D}={ac}−\frac{{b}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\begin{cases}{\mathrm{ellipse};\:{D}>\mathrm{0}}\\{\mathrm{parabola};\:{D}=\mathrm{0}}\\{\mathrm{hyperbola};\:{D}<\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\:\left(\mathrm{1}\right)\:\:{ac}−\frac{{b}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0} \\ $$$$\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\in\mathrm{par}\:\Rightarrow\:\left(\mathrm{2}\right)\:\:{f}=\mathrm{0} \\ $$$$\begin{pmatrix}{{p}}\\{\mathrm{0}}\end{pmatrix}\:\in\mathrm{par}\:\Rightarrow\:\left(\mathrm{3}\right)\:\:{ap}^{\mathrm{2}} +{dp}+{f}=\mathrm{0} \\ $$$$\begin{pmatrix}{\mathrm{0}}\\{{q}}\end{pmatrix}\:\in\mathrm{par}\:\Rightarrow\:\left(\mathrm{4}\right)\:\:{cq}^{\mathrm{2}} +{eq}+{f}=\mathrm{0} \\ $$$$\left(\mathrm{5}\right)\:\:\mathrm{we}\:\mathrm{know}\:\mathrm{the}\:\mathrm{shape}\:\mathrm{is}\:\mathrm{similar}\:\mathrm{to}\:{y}={x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\mathrm{the}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{rotation}:\:\mathrm{tan}\:\mathrm{2}\theta\:=\frac{{b}}{{a}−{c}};\:\mathrm{if}\:{b}={c}\:\Rightarrow \\ $$$$\:\:\:\:\:\Rightarrow\:\theta=\mathrm{45}° \\ $$$$\:\:\:\:\:\mathrm{usually}\:\mathrm{we}\:\mathrm{rotate}\:\mathrm{like}\:\mathrm{this}:\:\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:=\begin{pmatrix}{{x}'\mathrm{cos}\:\theta\:−{y}'\mathrm{sin}\:\theta}\\{{x}'\mathrm{sin}\:\theta\:+{y}'\mathrm{cos}\:\theta}\end{pmatrix} \\ $$$$\:\:\:\:\:\mathrm{and}\:\mathrm{get} \\ $$$$\:\:\:\:\:{ax}^{\mathrm{2}} +{bxy}+{cy}^{\mathrm{2}} +{dx}+{ey}+{f}=\mathrm{0}\:\rightarrow \\ $$$$\:\:\:\:\:\rightarrow\:{Ax}'^{\mathrm{2}} +{Cy}'^{\mathrm{2}} +{Dx}'+{Ey}'+{F} \\ $$$$\:\:\:\:\:\mathrm{and}\:\mathrm{then}\:\mathrm{complete}\:\mathrm{the}\:\mathrm{squares}\:\mathrm{to}\:\mathrm{see}\:\mathrm{the} \\ $$$$\:\:\:\:\:\mathrm{translation}\:\mathrm{in}\:{x}\:\mathrm{and}\:{y}\:\mathrm{directions} \\ $$$$\:\:\:\:\:\mathrm{here}\:\mathrm{we}\:\mathrm{have}\:\left({y}'−{n}\right)=\left({x}'−{m}\right)^{\mathrm{2}} \:\rightarrow \\ $$$$\:\:\:\:\:\rightarrow\:{x}'^{\mathrm{2}} −\mathrm{2}{mx}'−{y}'+\left({m}^{\mathrm{2}} −{n}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\Rightarrow\:{A}=\mathrm{1};\:{C}=\mathrm{0};\:{D}=−\mathrm{2}{m};\:{E}=−\mathrm{1};\:{F}={m}^{\mathrm{2}} −{n} \\ $$$$\:\:\:\:\:\mathrm{now}\:\mathrm{we}\:\mathrm{must}\:\mathrm{find}\:\theta \\ $$$$\:\:\:\:\:\mathrm{I}\:\mathrm{stop}\:\mathrm{here}\:\mathrm{and}\:\mathrm{go}\:\mathrm{to}\:\mathrm{bed}.\:\mathrm{this}\:\mathrm{is}\:\mathrm{what}'\mathrm{s} \\ $$$$\:\:\:\:\:\mathrm{already}\:\mathrm{there}: \\ $$$$\left(\mathrm{1}\right)\:\:{ac}−\frac{{b}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\:{f}=\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\:{ap}+{d}=\mathrm{0} \\ $$$$\left(\mathrm{4}\right)\:\:{cq}+{e}=\mathrm{0} \\ $$
Commented by TawaTawa1 last updated on 23/Apr/20
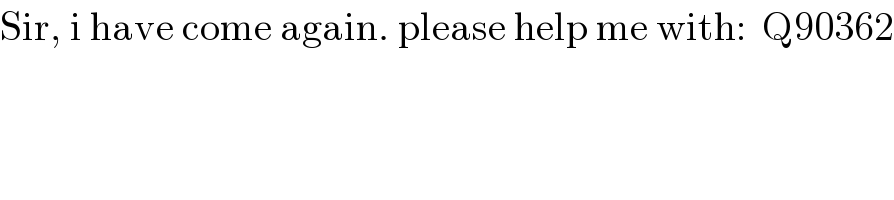
Sir, i have come again. please help me with: Q90362
$$\mathrm{Sir},\:\mathrm{i}\:\mathrm{have}\:\mathrm{come}\:\mathrm{again}.\:\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{with}:\:\:\mathrm{Q90362} \\ $$
Commented by TawaTawa1 last updated on 23/Apr/20
Please. God bless you more for everytime.
$$\mathrm{Please}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{more}\:\mathrm{for}\:\mathrm{everytime}. \\ $$
Commented by mr W last updated on 23/Apr/20
thank you MJS sir!
$${thank}\:{you}\:{MJS}\:{sir}! \\ $$
Answered by ajfour last updated on 23/Apr/20
Commented by ajfour last updated on 23/Apr/20
((y−mx−c)/( (√(1+m^2 ))))=(√((x−h)^2 +(y−k)^2 )) O(0,0), A(a,0), B(0,b) lie on parabola. ⇒ h^2 +k^2 =(c^2 /(1+m^2 )) ....(i) (a−h)^2 +k^2 =(((−am−c)^2 )/(1+m^2 )) ..(ii) h^2 +(b−k)^2 =(((b−c)^2 )/(1+m^2 )) ...(iii) And since this parabola has same shape as x^2 =4((1/4))y ((k−mh−c)/( (√(1+m^2 ))))=(1/2) ....(iv) Again using (i) in (ii) a^2 −2ah = ((a^2 m^2 +2amc)/(1+m^2 )) h=(((a/2)−cm)/(1+m^2 )) ......(I) in (iii): b^2 −2bk =((b^2 −2bc)/(1+m^2 )) k=((((bm^2 )/2)+c)/(1+m^2 )) .....(II) and ((−c)/( (√(1+m^2 ))))=(√(h^2 +k^2 )) = (1/2)+((mh−k)/( (√(1+m^2 )))) (c^2 /(1+m^2 ))=((((a/2)−cm)/(1+m^2 )))^2 +(((((bm^2 )/2)+c)/(1+m^2 )))^2 ⇒ (a^2 /4)−acm+((b^2 m^4 )/4)+bcm^2 =0 c=((a^2 +b^2 m^4 )/(4m(a−bm))) .......(III) and ((((bm^2 )/2)+c)/(1+m^2 ))−m((((a/2)−cm)/(1+m^2 )))−c=((√(1+m^2 ))/2) ⇒ bm^2 −am=(1+m^2 )^(3/2) ....(IV) herefrom we get m. then c, and then h,k using eqs. (III), (II), and (I). Eq. of parabola is ((y−mx−c)/( (√(1+m^2 ))))=(√((x−h)^2 +(y−k)^2 )) ■
$$\frac{{y}−{mx}−{c}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}=\sqrt{\left({x}−{h}\right)^{\mathrm{2}} +\left({y}−{k}\right)^{\mathrm{2}} } \\ $$$${O}\left(\mathrm{0},\mathrm{0}\right),\:{A}\left({a},\mathrm{0}\right),\:{B}\left(\mathrm{0},{b}\right)\:\:{lie}\:{on}\: \\ $$$${parabola}. \\ $$$$\Rightarrow\:\:{h}^{\mathrm{2}} +{k}^{\mathrm{2}} =\frac{{c}^{\mathrm{2}} }{\mathrm{1}+{m}^{\mathrm{2}} }\:\:\:\:\:\:\:….\left({i}\right) \\ $$$$\:\:\left({a}−{h}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} =\frac{\left(−{am}−{c}\right)^{\mathrm{2}} }{\mathrm{1}+{m}^{\mathrm{2}} }\:\:\:..\left({ii}\right) \\ $$$$\:\:\:\:\:{h}^{\mathrm{2}} +\left({b}−{k}\right)^{\mathrm{2}} =\frac{\left({b}−{c}\right)^{\mathrm{2}} }{\mathrm{1}+{m}^{\mathrm{2}} }\:\:\:\:…\left({iii}\right) \\ $$$${And}\:{since}\:{this}\:{parabola}\:{has} \\ $$$${same}\:{shape}\:{as}\:{x}^{\mathrm{2}} =\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{4}}\right){y} \\ $$$$\:\:\:\frac{{k}−{mh}−{c}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:….\left({iv}\right) \\ $$$${Again}\:\:{using}\:\left({i}\right)\:{in}\:\left({ii}\right) \\ $$$${a}^{\mathrm{2}} −\mathrm{2}{ah}\:=\:\frac{{a}^{\mathrm{2}} {m}^{\mathrm{2}} +\mathrm{2}{amc}}{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$$\:\:{h}=\frac{\frac{{a}}{\mathrm{2}}−{cm}}{\mathrm{1}+{m}^{\mathrm{2}} }\:\:\:\:\:\:……\left({I}\right) \\ $$$${in}\:\left({iii}\right): \\ $$$${b}^{\mathrm{2}} −\mathrm{2}{bk}\:=\frac{{b}^{\mathrm{2}} −\mathrm{2}{bc}}{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$$\:\:{k}=\frac{\frac{{bm}^{\mathrm{2}} }{\mathrm{2}}+{c}}{\mathrm{1}+{m}^{\mathrm{2}} }\:\:\:\:\:\:\:…..\left({II}\right) \\ $$$${and}\:\:\:\frac{−{c}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}=\sqrt{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{{mh}−{k}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }} \\ $$$$\:\:\:\frac{{c}^{\mathrm{2}} }{\mathrm{1}+{m}^{\mathrm{2}} }=\left(\frac{\frac{{a}}{\mathrm{2}}−{cm}}{\mathrm{1}+{m}^{\mathrm{2}} }\right)^{\mathrm{2}} +\left(\frac{\frac{{bm}^{\mathrm{2}} }{\mathrm{2}}+{c}}{\mathrm{1}+{m}^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{{a}^{\mathrm{2}} }{\mathrm{4}}−{acm}+\frac{{b}^{\mathrm{2}} {m}^{\mathrm{4}} }{\mathrm{4}}+{bcm}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:{c}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}^{\mathrm{4}} }{\mathrm{4}{m}\left({a}−{bm}\right)}\:\:\:\:\:…….\left({III}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$${and} \\ $$$$\:\:\frac{\frac{{bm}^{\mathrm{2}} }{\mathrm{2}}+{c}}{\mathrm{1}+{m}^{\mathrm{2}} }−{m}\left(\frac{\frac{{a}}{\mathrm{2}}−{cm}}{\mathrm{1}+{m}^{\mathrm{2}} }\right)−{c}=\frac{\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\Rightarrow\:\:{bm}^{\mathrm{2}} −{am}=\left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} \:\:\:….\left({IV}\right) \\ $$$${herefrom}\:\:{we}\:{get}\:{m}. \\ $$$${then}\:{c},\:{and}\:{then}\:{h},{k}\:\:{using}\:{eqs}. \\ $$$$\left({III}\right),\:\left({II}\right),\:{and}\:\left({I}\right). \\ $$$${Eq}.\:{of}\:{parabola}\:{is} \\ $$$$\frac{{y}−{mx}−{c}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}=\sqrt{\left({x}−{h}\right)^{\mathrm{2}} +\left({y}−{k}\right)^{\mathrm{2}} } \\ $$$$\blacksquare \\ $$
Commented by mr W last updated on 23/Apr/20
thanks alot sir! i′ll attempt a similar way.
$${thanks}\:{alot}\:{sir}!\:{i}'{ll}\:{attempt}\:{a}\:{similar} \\ $$$${way}. \\ $$
Commented by ajfour last updated on 23/Apr/20
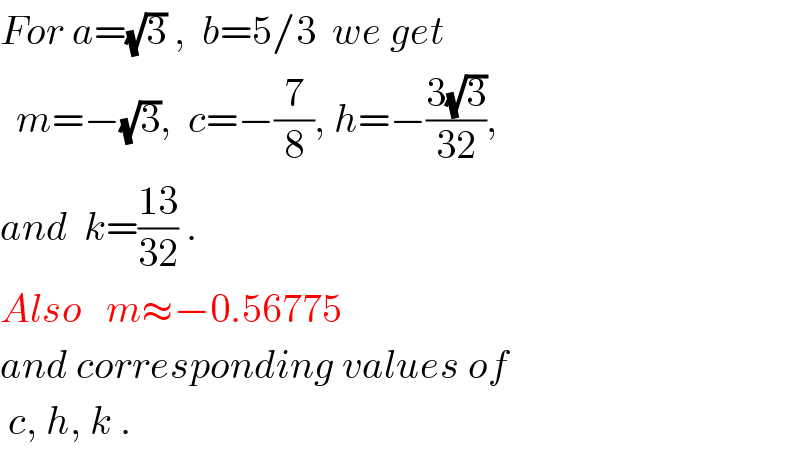
For a=(√3) , b=5/3 we get m=−(√3), c=−(7/8), h=−((3(√3))/(32)), and k=((13)/(32)) . Also m≈−0.56775 and corresponding values of c, h, k .
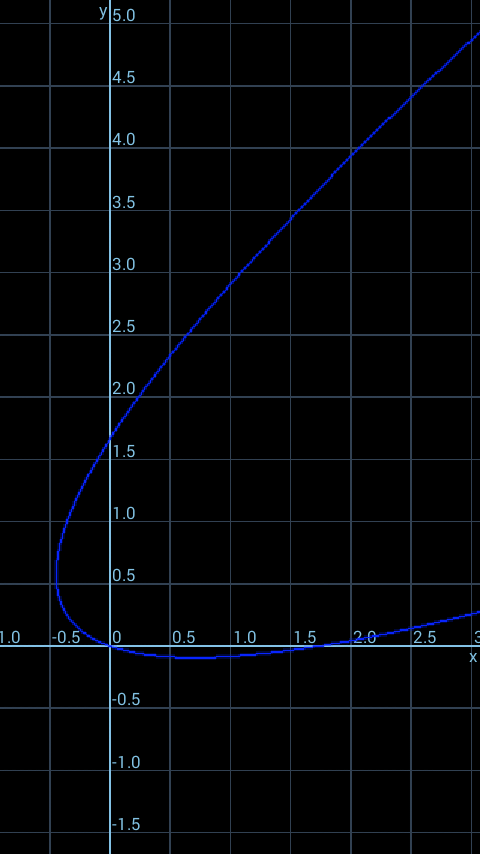
$${For}\:{a}=\sqrt{\mathrm{3}}\:,\:\:{b}=\mathrm{5}/\mathrm{3}\:\:{we}\:{get} \\ $$$$\:\:{m}=−\sqrt{\mathrm{3}},\:\:{c}=−\frac{\mathrm{7}}{\mathrm{8}},\:{h}=−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{32}}, \\ $$$${and}\:\:{k}=\frac{\mathrm{13}}{\mathrm{32}}\:. \\ $$$${Also}\:\:\:{m}\approx−\mathrm{0}.\mathrm{56775} \\ $$$${and}\:{corresponding}\:{values}\:{of} \\ $$$$\:{c},\:{h},\:{k}\:. \\ $$
Commented by ajfour last updated on 23/Apr/20
Answered by mr W last updated on 23/Apr/20
Commented by mr W last updated on 23/Apr/20
since the parabola has the same shape as y=x^2 , it can be obtained from y=x^2 through some transformation: translation: vertex from O(0,0) to O′(−h,−h^2 ) y=x^2 ⇒ y=x^2 −2hx rotation: about O by angle θ ⇒ x sin θ+y cos θ=(x cos θ−y sin θ)^2 −2h(x cos θ−y sin θ) since this transformed parabola passes through (a,0) and (0,b), we get: b cos θ=(−b sin θ)^2 −2h(−b sin θ) cos θ=b sin^2 θ+2h sin θ ⇒h=(1/2)((1/(tan θ))−b sin θ) ...(i) a sin θ=(a cos θ)^2 −2h(a cos θ) sin θ=a cos^2 θ−2h cos θ ⇒h=(1/2)(a cos θ−tan θ) ...(ii) (1/(tan θ))−b sin θ=a cos θ−tan θ ⇒ (1/(tan θ))+tan θ=a cos θ+b sin θ ..(iii) eqn. of parabola: x sin θ+y cos θ=(x cos θ−y sin θ)^2 −(a cos θ−tan θ)(x cos θ−y sin θ) usually (iii) has two roots for θ, that means we have usually two possible parabolas, see examples:
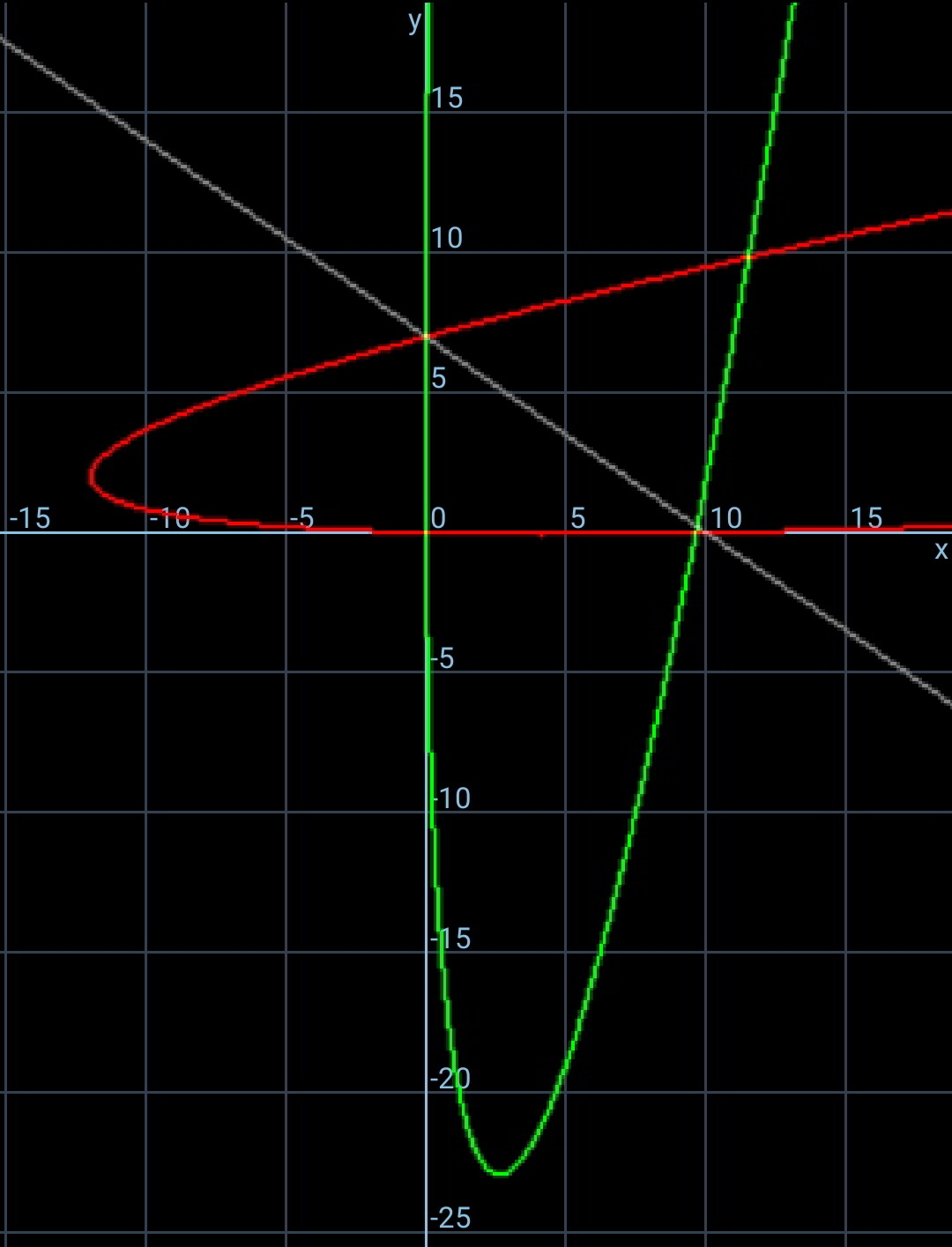
$${since}\:{the}\:{parabola}\:{has}\:{the}\:{same}\:{shape} \\ $$$${as}\:{y}={x}^{\mathrm{2}} ,\:{it}\:{can}\:{be}\:{obtained}\:{from}\:{y}={x}^{\mathrm{2}} \\ $$$${through}\:{some}\:{transformation}: \\ $$$${translation}:\:{vertex}\:{from}\:{O}\left(\mathrm{0},\mathrm{0}\right)\:{to}\:{O}'\left(−{h},−{h}^{\mathrm{2}} \right) \\ $$$${y}={x}^{\mathrm{2}} \:\Rightarrow\:{y}={x}^{\mathrm{2}} −\mathrm{2}{hx} \\ $$$${rotation}:\:{about}\:{O}\:{by}\:{angle}\:\theta \\ $$$$\Rightarrow\:{x}\:\mathrm{sin}\:\theta+{y}\:\mathrm{cos}\:\theta=\left({x}\:\mathrm{cos}\:\theta−{y}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} −\mathrm{2}{h}\left({x}\:\mathrm{cos}\:\theta−{y}\:\mathrm{sin}\:\theta\right) \\ $$$$ \\ $$$${since}\:{this}\:{transformed}\:{parabola} \\ $$$${passes}\:{through}\:\left({a},\mathrm{0}\right)\:{and}\:\left(\mathrm{0},{b}\right),\:{we}\:{get}: \\ $$$${b}\:\mathrm{cos}\:\theta=\left(−{b}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} −\mathrm{2}{h}\left(−{b}\:\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{cos}\:\theta={b}\:\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{2}{h}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{h}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{tan}\:\theta}−{b}\:\mathrm{sin}\:\theta\right)\:\:\:…\left({i}\right) \\ $$$${a}\:\mathrm{sin}\:\theta=\left({a}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} −\mathrm{2}{h}\left({a}\:\mathrm{cos}\:\theta\right) \\ $$$$\mathrm{sin}\:\theta={a}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{2}{h}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{h}=\frac{\mathrm{1}}{\mathrm{2}}\left({a}\:\mathrm{cos}\:\theta−\mathrm{tan}\:\theta\right)\:\:\:…\left({ii}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\theta}−{b}\:\mathrm{sin}\:\theta={a}\:\mathrm{cos}\:\theta−\mathrm{tan}\:\theta \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{tan}\:\theta}+\mathrm{tan}\:\theta={a}\:\mathrm{cos}\:\theta+{b}\:\mathrm{sin}\:\theta\:\:\:..\left({iii}\right) \\ $$$$ \\ $$$${eqn}.\:{of}\:{parabola}: \\ $$$${x}\:\mathrm{sin}\:\theta+{y}\:\mathrm{cos}\:\theta=\left({x}\:\mathrm{cos}\:\theta−{y}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} −\left({a}\:\mathrm{cos}\:\theta−\mathrm{tan}\:\theta\right)\left({x}\:\mathrm{cos}\:\theta−{y}\:\mathrm{sin}\:\theta\right) \\ $$$$ \\ $$$${usually}\:\left({iii}\right)\:{has}\:{two}\:{roots}\:{for}\:\theta, \\ $$$${that}\:{means}\:{we}\:{have}\:{usually}\:{two} \\ $$$${possible}\:{parabolas},\:{see}\:{examples}: \\ $$
Commented by mr W last updated on 23/Apr/20
Commented by mr W last updated on 23/Apr/20
Commented by mr W last updated on 23/Apr/20
Commented by ajfour last updated on 23/Apr/20
Its very nice, short and wise way Sir; thanks a lot.
$${Its}\:{very}\:{nice},\:{short}\:{and}\:{wise} \\ $$$${way}\:{Sir};\:\:{thanks}\:{a}\:{lot}. \\ $$
Commented by mr W last updated on 23/Apr/20
Commented by mr W last updated on 23/Apr/20
in general a right−angled triangle can be inscribed in the parabola in two different ways, therefore we have two possible positions for the parabola. there is only one solution if a=b=(√2).
$${in}\:{general}\:{a}\:{right}−{angled}\:{triangle} \\ $$$${can}\:{be}\:{inscribed}\:{in}\:{the}\:{parabola}\:{in} \\ $$$${two}\:{different}\:{ways},\:{therefore}\:{we} \\ $$$${have}\:{two}\:{possible}\:{positions}\:{for}\:{the} \\ $$$${parabola}. \\ $$$${there}\:{is}\:{only}\:{one}\:{solution}\:{if}\:{a}={b}=\sqrt{\mathrm{2}}. \\ $$
Commented by ajfour last updated on 24/Apr/20
too good interpretation, and explanation, Sir!
$${too}\:{good}\:{interpretation},\:{and} \\ $$$${explanation},\:{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *