Question Number 90402 by bshahid010@gmail.com last updated on 23/Apr/20
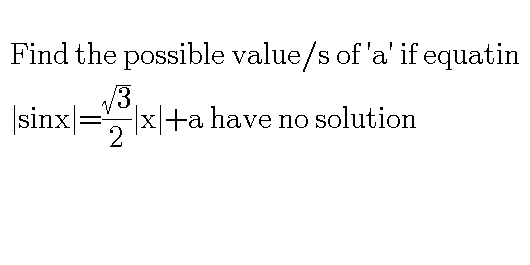
Answered by MJS last updated on 23/Apr/20
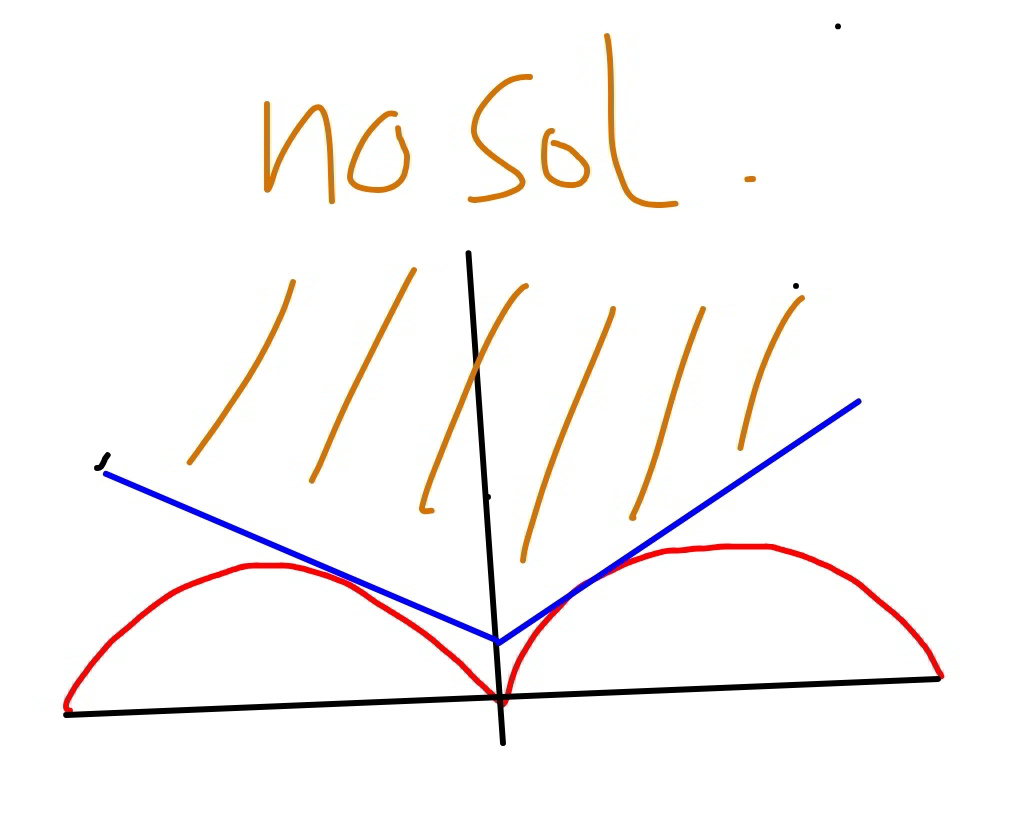
![for 0≤x≤1: (d/dx)[sin x −((√3)/2)x]=cos x −((√3)/2) cos x =((√3)/2) ⇒ x=(π/6) sin (π/6) −((√3)/2)×(π/6)=(1/2)−((π(√3))/(12)) ⇒ no solution for a<((π(√3))/(12))−(1/2)](https://www.tinkutara.com/question/Q90439.png)
$$\mathrm{for}\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}:\:\frac{{d}}{{dx}}\left[\mathrm{sin}\:{x}\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{x}\right]=\mathrm{cos}\:{x}\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:{x}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow\:{x}=\frac{\pi}{\mathrm{6}} \\ $$$$\mathrm{sin}\:\frac{\pi}{\mathrm{6}}\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\pi}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{12}} \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{solution}\:\mathrm{for}\:{a}<\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 23/Apr/20
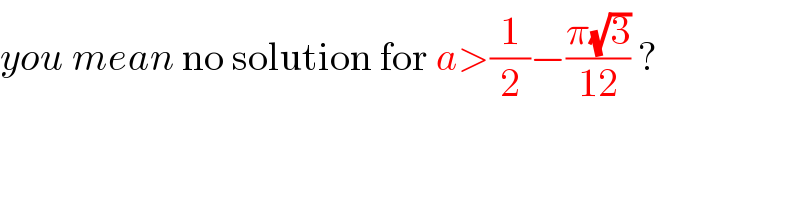
$${you}\:{mean}\:\mathrm{no}\:\mathrm{solution}\:\mathrm{for}\:{a}>\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{12}}\:? \\ $$
Commented by mr W last updated on 23/Apr/20