Question Number 90514 by I want to learn more last updated on 24/Apr/20
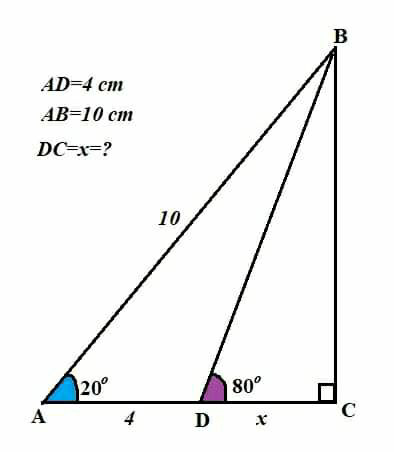
Commented by $@ty@m123 last updated on 24/Apr/20
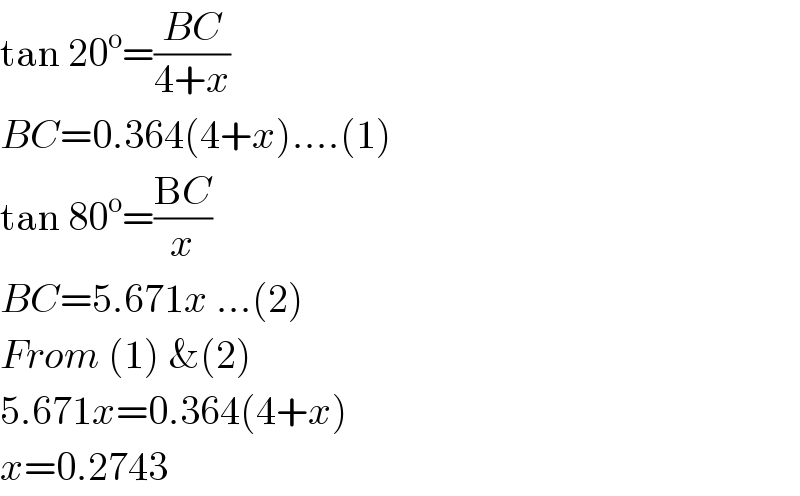
$$\mathrm{tan}\:\mathrm{20}^{\mathrm{o}} =\frac{{BC}}{\mathrm{4}+{x}} \\ $$$${BC}=\mathrm{0}.\mathrm{364}\left(\mathrm{4}+{x}\right)….\left(\mathrm{1}\right) \\ $$$$\mathrm{tan}\:\mathrm{80}^{\mathrm{o}} =\frac{\mathrm{B}{C}}{{x}} \\ $$$${BC}=\mathrm{5}.\mathrm{671}{x}\:…\left(\mathrm{2}\right) \\ $$$${From}\:\left(\mathrm{1}\right)\:\&\left(\mathrm{2}\right) \\ $$$$\mathrm{5}.\mathrm{671}{x}=\mathrm{0}.\mathrm{364}\left(\mathrm{4}+{x}\right) \\ $$$${x}=\mathrm{0}.\mathrm{2743} \\ $$
Commented by me2love2math last updated on 24/Apr/20
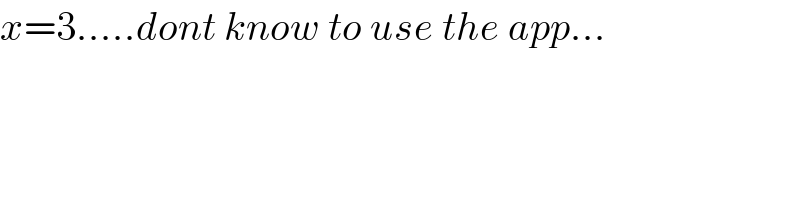
$${x}=\mathrm{3}…..{dont}\:{know}\:{to}\:{use}\:{the}\:{app}… \\ $$
Commented by $@ty@m123 last updated on 24/Apr/20
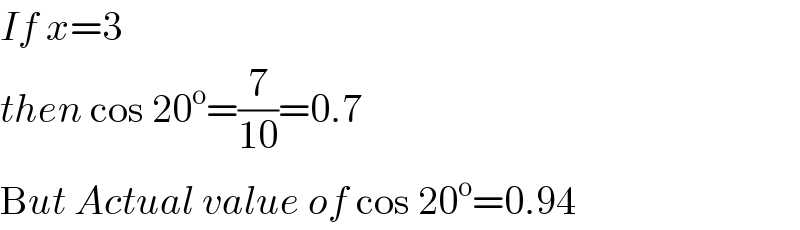
$${If}\:{x}=\mathrm{3}\: \\ $$$${then}\:\mathrm{cos}\:\mathrm{20}^{\mathrm{o}} =\frac{\mathrm{7}}{\mathrm{10}}=\mathrm{0}.\mathrm{7} \\ $$$$\mathrm{B}{ut}\:{Actual}\:{value}\:{of}\:\mathrm{cos}\:\mathrm{20}^{\mathrm{o}} =\mathrm{0}.\mathrm{94} \\ $$
Commented by me2love2math last updated on 24/Apr/20
$${the}\:{triangle}\:{is}\:{not}\:{complete}….{extend}\: \\ $$$${the}\:{diagram}\:{and}\:{apply}\:{triangle}\:{theorem} \\ $$
Commented by I want to learn more last updated on 24/Apr/20
$$\mathrm{Thanks}\:\mathrm{sirs},\:\mathrm{but}\:\mathrm{which}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{please}. \\ $$
Commented by me2love2math last updated on 24/Apr/20
$${my}\:{English}\:{bad}\:{but}\:{my}\:{maths}\:{is}\:{good} \\ $$$${I}\:{want}\:{to}\:{learn}\:{how}\:{to}\:{use}\:{the}\:{app} \\ $$
Answered by mahdi last updated on 24/Apr/20
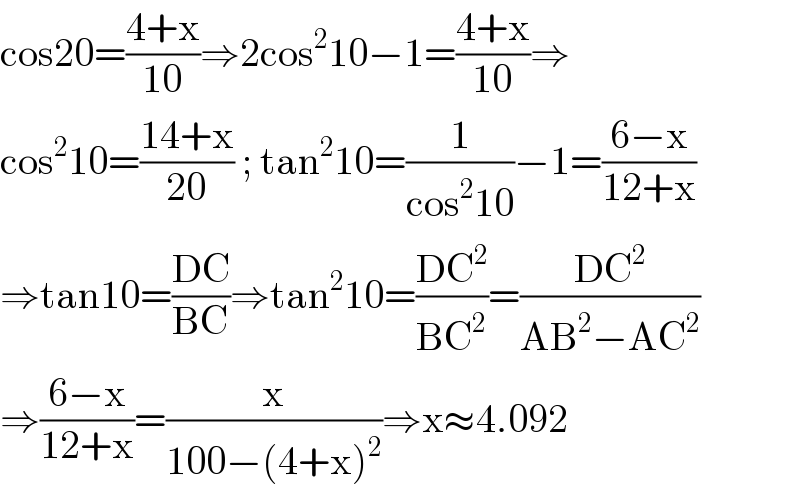
$$\mathrm{cos20}=\frac{\mathrm{4}+\mathrm{x}}{\mathrm{10}}\Rightarrow\mathrm{2cos}^{\mathrm{2}} \mathrm{10}−\mathrm{1}=\frac{\mathrm{4}+\mathrm{x}}{\mathrm{10}}\Rightarrow \\ $$$$\mathrm{cos}^{\mathrm{2}} \mathrm{10}=\frac{\mathrm{14}+\mathrm{x}}{\mathrm{20}}\:;\:\mathrm{tan}^{\mathrm{2}} \mathrm{10}=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{10}}−\mathrm{1}=\frac{\mathrm{6}−\mathrm{x}}{\mathrm{12}+\mathrm{x}} \\ $$$$\Rightarrow\mathrm{tan10}=\frac{\mathrm{DC}}{\mathrm{BC}}\Rightarrow\mathrm{tan}^{\mathrm{2}} \mathrm{10}=\frac{\mathrm{DC}^{\mathrm{2}} }{\mathrm{BC}^{\mathrm{2}} }=\frac{\mathrm{DC}^{\mathrm{2}} }{\mathrm{AB}^{\mathrm{2}} −\mathrm{AC}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{6}−\mathrm{x}}{\mathrm{12}+\mathrm{x}}=\frac{\mathrm{x}}{\mathrm{100}−\left(\mathrm{4}+\mathrm{x}\right)^{\mathrm{2}} }\Rightarrow\mathrm{x}\approx\mathrm{4}.\mathrm{092} \\ $$
Commented by I want to learn more last updated on 24/Apr/20

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{we}\:\mathrm{are}\:\mathrm{having}\:\mathrm{different}\:\mathrm{amswers}\:\mathrm{sir}. \\ $$$$\mathrm{which}\:\mathrm{one}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{please} \\ $$
Commented by mr W last updated on 24/Apr/20

$${your}\:{question}\:{is}\:{wrong}!\:{so}\:{you}\:{can}'{t} \\ $$$${get}\:{one}\:{correct}\:{answer}! \\ $$
Answered by mr W last updated on 24/Apr/20

$${question}\:{is}\:{wrong}! \\ $$$${AD}=\mathrm{4}\:{is}\:{wrong}\:{or}\:\angle{BDC}=\mathrm{80}°\:{is}\:{wrong}! \\ $$$$ \\ $$$${say}\:{AD}=\mathrm{4}\:{is}\:{correct},\:{then} \\ $$$${AC}=\mathrm{10}×\mathrm{cos}\:\mathrm{20}° \\ $$$${BC}=\mathrm{10}×\mathrm{sin}\:\mathrm{20}° \\ $$$${x}=\mathrm{10}×\mathrm{cos}\:\mathrm{20}°−\mathrm{4} \\ $$$$\mathrm{tan}\:\angle{BDC}=\frac{\mathrm{10}×\mathrm{sin}\:\mathrm{20}°}{\mathrm{10}×\mathrm{cos}\:\mathrm{20}°−\mathrm{4}} \\ $$$$\angle{BDC}=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{10}×\mathrm{sin}\:\mathrm{20}°}{\mathrm{10}×\mathrm{cos}\:\mathrm{20}°−\mathrm{4}}\right)=\mathrm{32}.\mathrm{363}°\neq\mathrm{80}° \\ $$
Commented by I want to learn more last updated on 25/Apr/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
