Question-90555

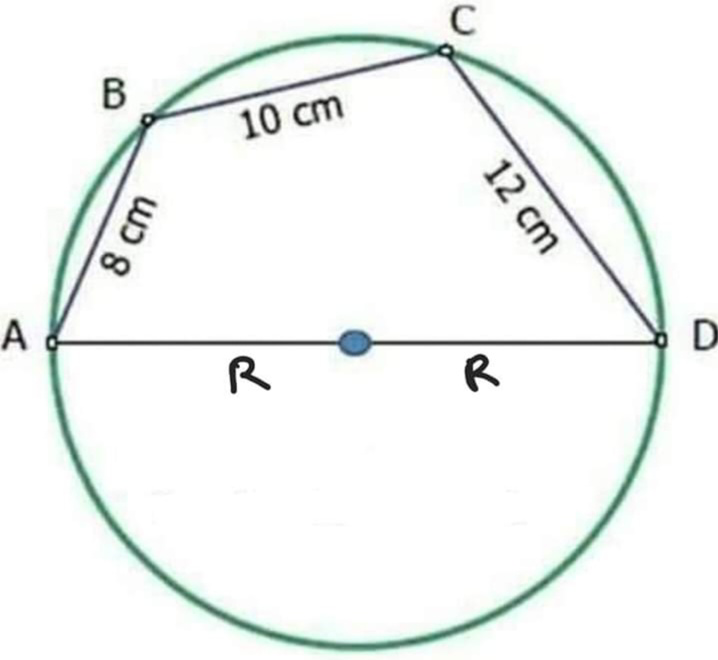
Question Number 90555 by naka3546 last updated on 24/Apr/20

Commented by jagoll last updated on 25/Apr/20

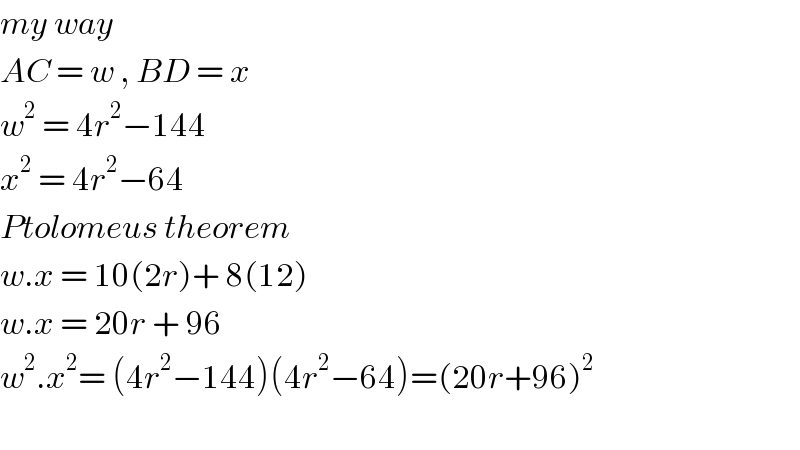
my way AC = w , BD = x w^2 = 4r^2 −144 x^2 = 4r^2 −64 Ptolomeus theorem w.x = 10(2r)+ 8(12) w.x = 20r + 96 w^2 .x^2 = (4r^2 −144)(4r^2 −64)=(20r+96)^2

$${my}\:{way} \\ $$$${AC}\:=\:{w}\:,\:{BD}\:=\:{x} \\ $$$${w}^{\mathrm{2}} \:=\:\mathrm{4}{r}^{\mathrm{2}} −\mathrm{144} \\ $$$${x}^{\mathrm{2}} \:=\:\mathrm{4}{r}^{\mathrm{2}} −\mathrm{64} \\ $$$${Ptolomeus}\:{theorem}\: \\ $$$${w}.{x}\:=\:\mathrm{10}\left(\mathrm{2}{r}\right)+\:\mathrm{8}\left(\mathrm{12}\right) \\ $$$${w}.{x}\:=\:\mathrm{20}{r}\:+\:\mathrm{96} \\ $$$${w}^{\mathrm{2}} .{x}^{\mathrm{2}} =\:\left(\mathrm{4}{r}^{\mathrm{2}} −\mathrm{144}\right)\left(\mathrm{4}{r}^{\mathrm{2}} −\mathrm{64}\right)=\left(\mathrm{20}{r}+\mathrm{96}\right)^{\mathrm{2}} \\ $$$$ \\ $$

Commented by jagoll last updated on 25/Apr/20

$${stuck}\:{in}\:{quartic}\:{equation} \\ $$

Answered by mr W last updated on 24/Apr/20

a=8 b=10 c=12 d=2R s=((8+10+12+2R)/2)=15+R R=(1/4)(√(((8×10+24R)(8×12+20R)(10×12+16R))/((15+R−8)(15+R−10)(15+R−12)(15+R−2R)))) R^2 =(((20+6R)(24+5R)(120+16R))/((7+R)(5+R)(3+R)(15−R))) R^3 −77R−240=0 ⇒R=((2(√(231)))/3) sin (−(1/3)sin^(−1) ((360(√(231)))/(5929))+((2π)/3))≈10.0446

$${a}=\mathrm{8} \\ $$$${b}=\mathrm{10} \\ $$$${c}=\mathrm{12} \\ $$$${d}=\mathrm{2}{R} \\ $$$${s}=\frac{\mathrm{8}+\mathrm{10}+\mathrm{12}+\mathrm{2}{R}}{\mathrm{2}}=\mathrm{15}+{R} \\ $$$${R}=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\frac{\left(\mathrm{8}×\mathrm{10}+\mathrm{24}{R}\right)\left(\mathrm{8}×\mathrm{12}+\mathrm{20}{R}\right)\left(\mathrm{10}×\mathrm{12}+\mathrm{16}{R}\right)}{\left(\mathrm{15}+{R}−\mathrm{8}\right)\left(\mathrm{15}+{R}−\mathrm{10}\right)\left(\mathrm{15}+{R}−\mathrm{12}\right)\left(\mathrm{15}+{R}−\mathrm{2}{R}\right)}} \\ $$$${R}^{\mathrm{2}} =\frac{\left(\mathrm{20}+\mathrm{6}{R}\right)\left(\mathrm{24}+\mathrm{5}{R}\right)\left(\mathrm{120}+\mathrm{16}{R}\right)}{\left(\mathrm{7}+{R}\right)\left(\mathrm{5}+{R}\right)\left(\mathrm{3}+{R}\right)\left(\mathrm{15}−{R}\right)} \\ $$$${R}^{\mathrm{3}} −\mathrm{77}{R}−\mathrm{240}=\mathrm{0} \\ $$$$\Rightarrow{R}=\frac{\mathrm{2}\sqrt{\mathrm{231}}}{\mathrm{3}}\:\mathrm{sin}\:\left(−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{360}\sqrt{\mathrm{231}}}{\mathrm{5929}}+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\approx\mathrm{10}.\mathrm{0446} \\ $$

Commented by jagoll last updated on 25/Apr/20