Menu Close

Question-90590

Tinku Tara 0 Comments
Pin




Question Number 90590 by mr W last updated on 24/Apr/20
Commented by mr W last updated on 24/Apr/20
prove that AD=2(√(ab))
$${prove}\:{that} \\ $$$${AD}=\mathrm{2}\sqrt{{ab}} \\ $$
Commented by john santu last updated on 25/Apr/20
ok. i can try
$${ok}.\:{i}\:{can}\:{try} \\ $$
Answered by mr W last updated on 25/Apr/20
Commented by mr W last updated on 25/Apr/20
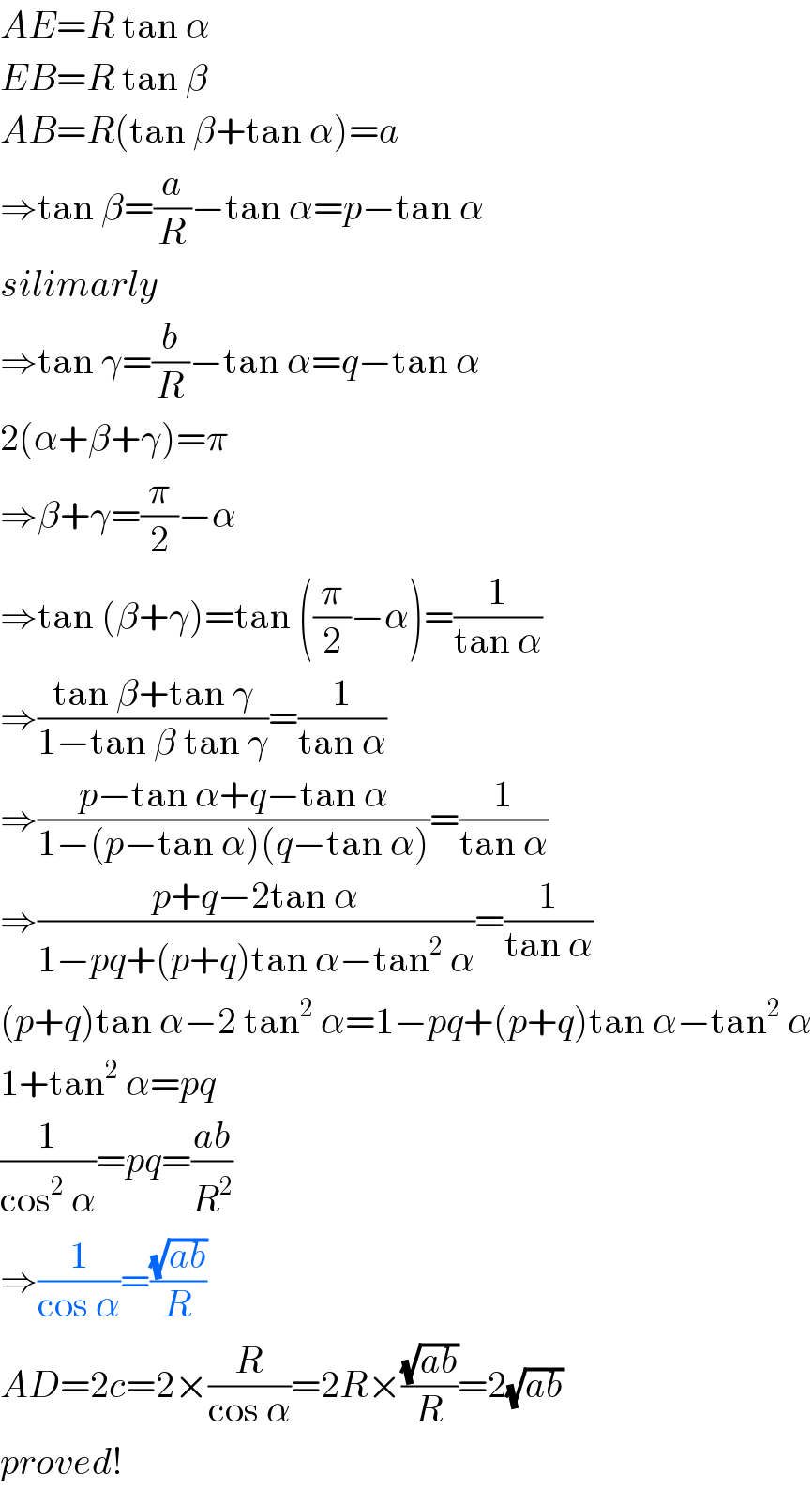
AE=R tan α EB=R tan β AB=R(tan β+tan α)=a ⇒tan β=(a/R)−tan α=p−tan α silimarly ⇒tan γ=(b/R)−tan α=q−tan α 2(α+β+γ)=π ⇒β+γ=(π/2)−α ⇒tan (β+γ)=tan ((π/2)−α)=(1/(tan α)) ⇒((tan β+tan γ)/(1−tan β tan γ))=(1/(tan α)) ⇒((p−tan α+q−tan α)/(1−(p−tan α)(q−tan α)))=(1/(tan α)) ⇒((p+q−2tan α)/(1−pq+(p+q)tan α−tan^2 α))=(1/(tan α)) (p+q)tan α−2 tan^2 α=1−pq+(p+q)tan α−tan^2 α 1+tan^2 α=pq (1/(cos^2 α))=pq=((ab)/R^2 ) ⇒(1/(cos α))=((√(ab))/R) AD=2c=2×(R/(cos α))=2R×((√(ab))/R)=2(√(ab)) proved!
$${AE}={R}\:\mathrm{tan}\:\alpha \\ $$$${EB}={R}\:\mathrm{tan}\:\beta \\ $$$${AB}={R}\left(\mathrm{tan}\:\beta+\mathrm{tan}\:\alpha\right)={a} \\ $$$$\Rightarrow\mathrm{tan}\:\beta=\frac{{a}}{{R}}−\mathrm{tan}\:\alpha={p}−\mathrm{tan}\:\alpha \\ $$$${silimarly} \\ $$$$\Rightarrow\mathrm{tan}\:\gamma=\frac{{b}}{{R}}−\mathrm{tan}\:\alpha={q}−\mathrm{tan}\:\alpha \\ $$$$\mathrm{2}\left(\alpha+\beta+\gamma\right)=\pi \\ $$$$\Rightarrow\beta+\gamma=\frac{\pi}{\mathrm{2}}−\alpha \\ $$$$\Rightarrow\mathrm{tan}\:\left(\beta+\gamma\right)=\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}−\alpha\right)=\frac{\mathrm{1}}{\mathrm{tan}\:\alpha} \\ $$$$\Rightarrow\frac{\mathrm{tan}\:\beta+\mathrm{tan}\:\gamma}{\mathrm{1}−\mathrm{tan}\:\beta\:\mathrm{tan}\:\gamma}=\frac{\mathrm{1}}{\mathrm{tan}\:\alpha} \\ $$$$\Rightarrow\frac{{p}−\mathrm{tan}\:\alpha+{q}−\mathrm{tan}\:\alpha}{\mathrm{1}−\left({p}−\mathrm{tan}\:\alpha\right)\left({q}−\mathrm{tan}\:\alpha\right)}=\frac{\mathrm{1}}{\mathrm{tan}\:\alpha} \\ $$$$\Rightarrow\frac{{p}+{q}−\mathrm{2tan}\:\alpha}{\mathrm{1}−{pq}+\left({p}+{q}\right)\mathrm{tan}\:\alpha−\mathrm{tan}^{\mathrm{2}} \:\alpha}=\frac{\mathrm{1}}{\mathrm{tan}\:\alpha} \\ $$$$\left({p}+{q}\right)\mathrm{tan}\:\alpha−\mathrm{2}\:\mathrm{tan}^{\mathrm{2}} \:\alpha=\mathrm{1}−{pq}+\left({p}+{q}\right)\mathrm{tan}\:\alpha−\mathrm{tan}^{\mathrm{2}} \:\alpha \\ $$$$\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\alpha={pq} \\ $$$$\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\alpha}={pq}=\frac{{ab}}{{R}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{cos}\:\alpha}=\frac{\sqrt{{ab}}}{{R}} \\ $$$${AD}=\mathrm{2}{c}=\mathrm{2}×\frac{{R}}{\mathrm{cos}\:\alpha}=\mathrm{2}{R}×\frac{\sqrt{{ab}}}{{R}}=\mathrm{2}\sqrt{{ab}} \\ $$$${proved}! \\ $$
Commented by I want to learn more last updated on 26/Apr/20
Just see this now, thanks sir
$$\mathrm{Just}\:\mathrm{see}\:\mathrm{this}\:\mathrm{now},\:\mathrm{thanks}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *