Question Number 90773 by ajfour last updated on 26/Apr/20
Commented by ajfour last updated on 26/Apr/20
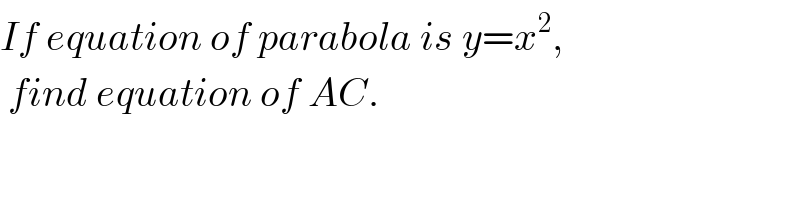
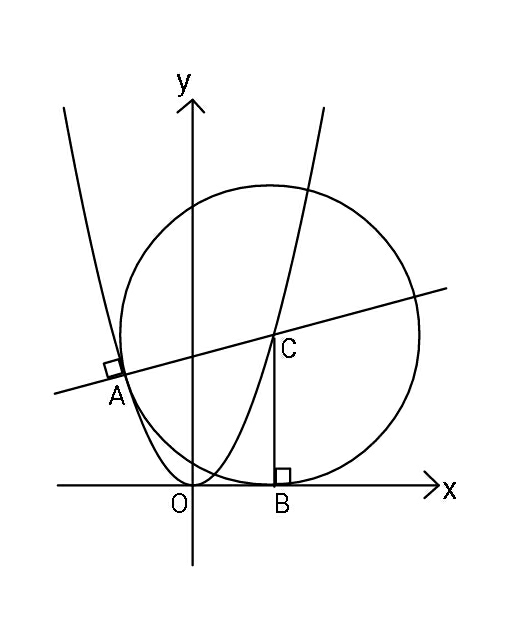
$${If}\:{equation}\:{of}\:{parabola}\:{is}\:{y}={x}^{\mathrm{2}} , \\ $$$$\:{find}\:{equation}\:{of}\:{AC}. \\ $$
Answered by mr W last updated on 26/Apr/20
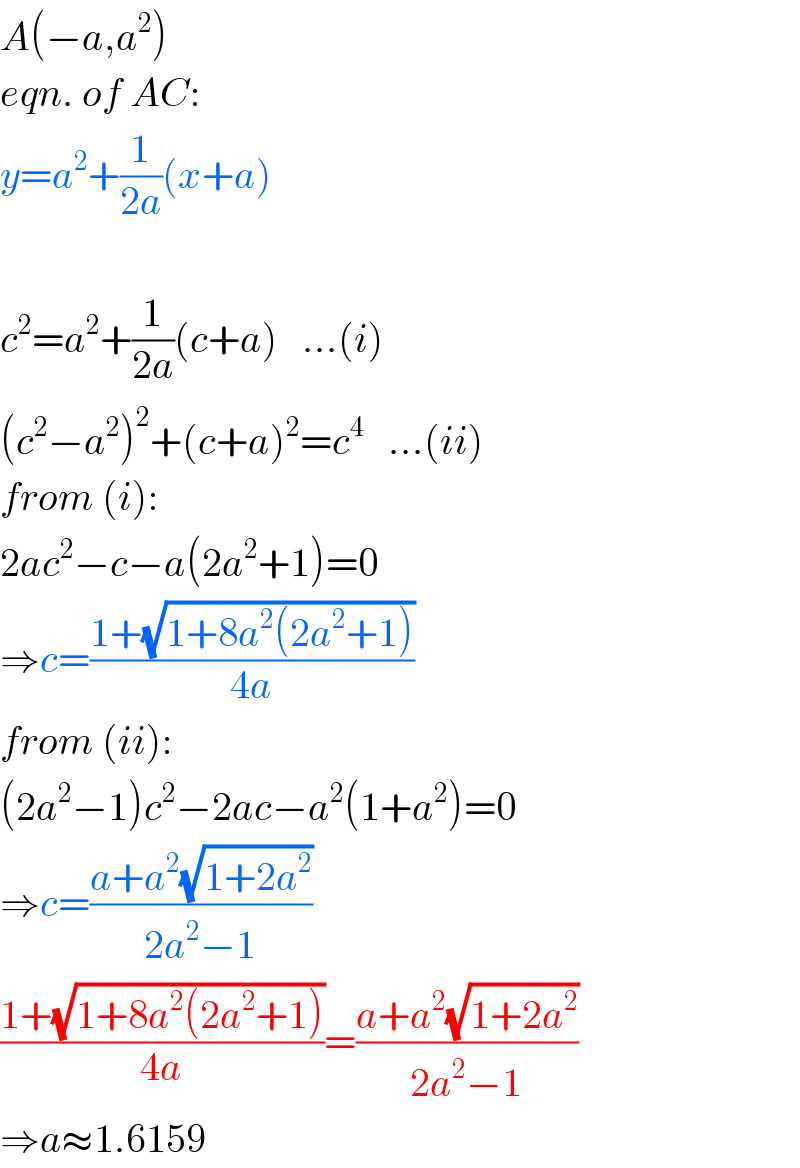
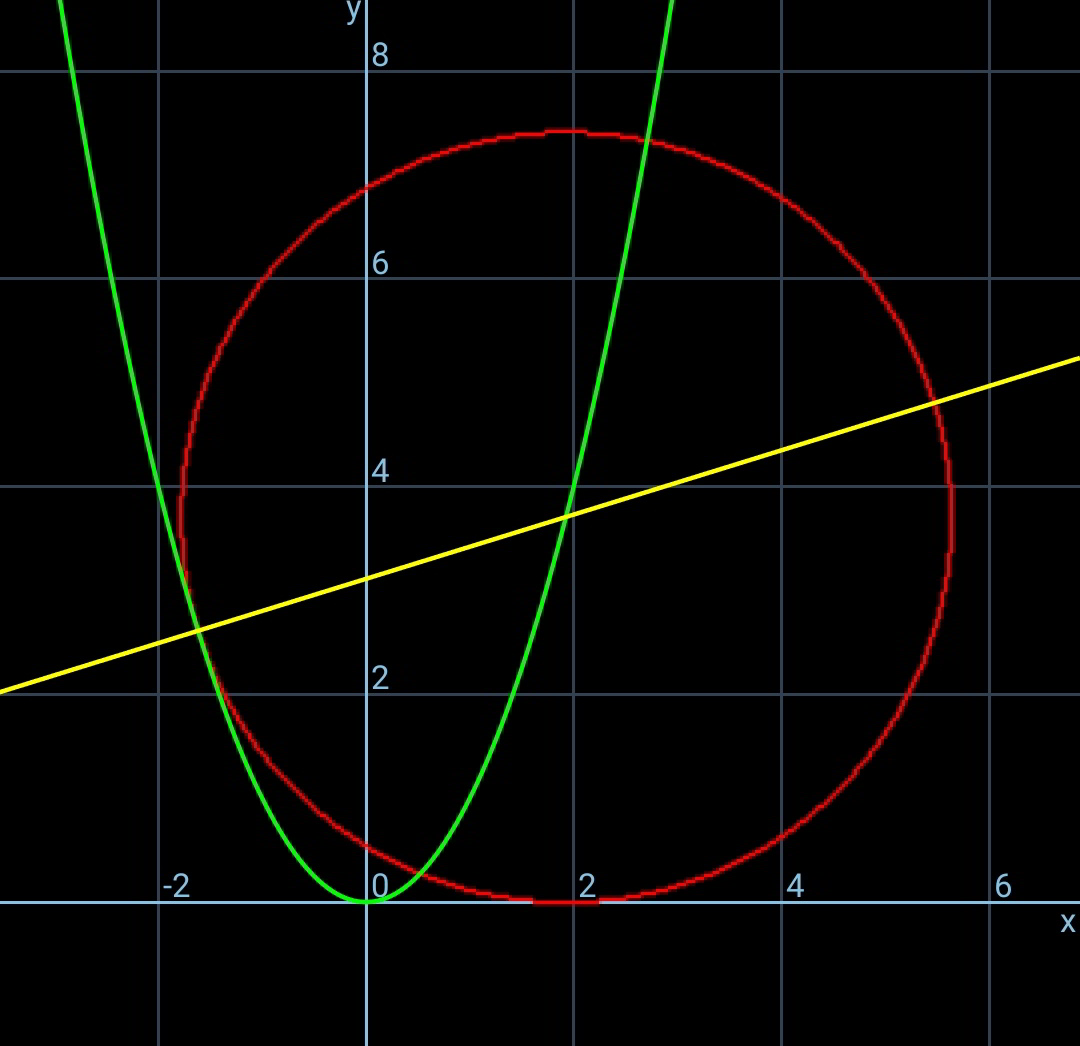
$${A}\left(−{a},{a}^{\mathrm{2}} \right) \\ $$$${eqn}.\:{of}\:{AC}: \\ $$$${y}={a}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}{a}}\left({x}+{a}\right) \\ $$$$ \\ $$$${c}^{\mathrm{2}} ={a}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}{a}}\left({c}+{a}\right)\:\:\:…\left({i}\right) \\ $$$$\left({c}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} +\left({c}+{a}\right)^{\mathrm{2}} ={c}^{\mathrm{4}} \:\:\:…\left({ii}\right) \\ $$$${from}\:\left({i}\right): \\ $$$$\mathrm{2}{ac}^{\mathrm{2}} −{c}−{a}\left(\mathrm{2}{a}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{c}=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{8}{a}^{\mathrm{2}} \left(\mathrm{2}{a}^{\mathrm{2}} +\mathrm{1}\right)}}{\mathrm{4}{a}} \\ $$$${from}\:\left({ii}\right): \\ $$$$\left(\mathrm{2}{a}^{\mathrm{2}} −\mathrm{1}\right){c}^{\mathrm{2}} −\mathrm{2}{ac}−{a}^{\mathrm{2}} \left(\mathrm{1}+{a}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{c}=\frac{{a}+{a}^{\mathrm{2}} \sqrt{\mathrm{1}+\mathrm{2}{a}^{\mathrm{2}} }}{\mathrm{2}{a}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{8}{a}^{\mathrm{2}} \left(\mathrm{2}{a}^{\mathrm{2}} +\mathrm{1}\right)}}{\mathrm{4}{a}}=\frac{{a}+{a}^{\mathrm{2}} \sqrt{\mathrm{1}+\mathrm{2}{a}^{\mathrm{2}} }}{\mathrm{2}{a}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Rightarrow{a}\approx\mathrm{1}.\mathrm{6159} \\ $$
Commented by mr W last updated on 26/Apr/20
Commented by ajfour last updated on 26/Apr/20
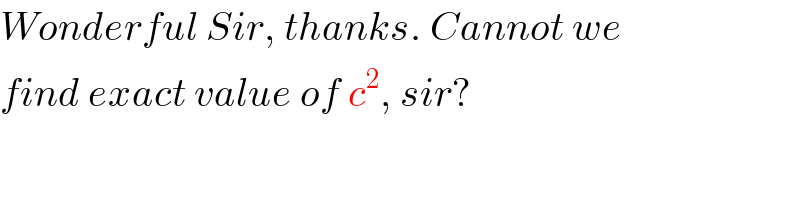
$${Wonderful}\:{Sir},\:{thanks}.\:{Cannot}\:{we}\: \\ $$$${find}\:{exact}\:{value}\:{of}\:{c}^{\mathrm{2}} ,\:{sir}? \\ $$
Commented by mr W last updated on 26/Apr/20

$${i}\:{think}\:{no}. \\ $$
Commented by ajfour last updated on 26/Apr/20
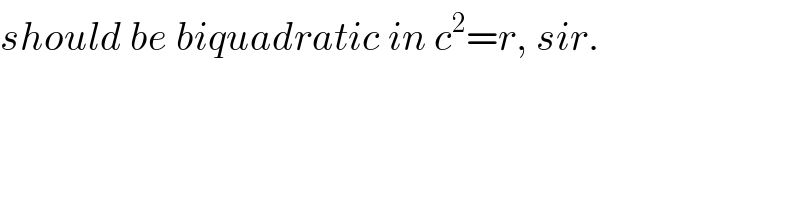
$${should}\:{be}\:{biquadratic}\:{in}\:{c}^{\mathrm{2}} ={r},\:{sir}. \\ $$
