Question Number 90904 by M±th+et+s last updated on 26/Apr/20

Commented by M±th+et+s last updated on 26/Apr/20
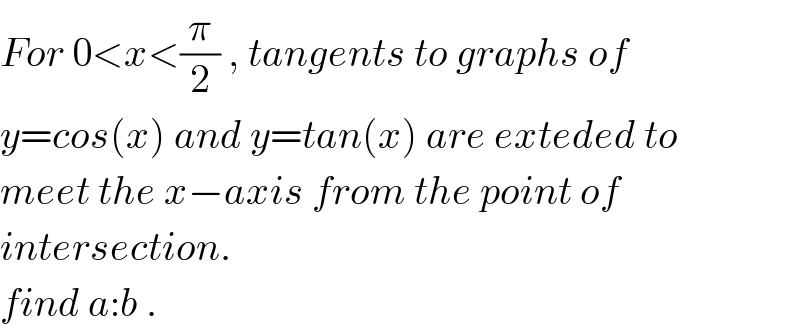
$${For}\:\mathrm{0}<{x}<\frac{\pi}{\mathrm{2}}\:,\:{tangents}\:{to}\:{graphs}\:{of} \\ $$$${y}={cos}\left({x}\right)\:{and}\:{y}={tan}\left({x}\right)\:{are}\:{exteded}\:{to} \\ $$$${meet}\:{the}\:{x}−{axis}\:{from}\:{the}\:{point}\:{of}\: \\ $$$${intersection}. \\ $$$${find}\:{a}:{b}\:. \\ $$
Answered by Kunal12588 last updated on 26/Apr/20

$${let}\:{intersection}\:{point}\:{be}\:\left({p},{q}\right) \\ $$$${tan}\:{p}\:=\:{cos}\:{p} \\ $$$${sin}^{\mathrm{2}} {p}+{sinp}−\mathrm{1}=\mathrm{0} \\ $$$${sin}\:{p}\:=\:\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}} \\ $$$${p}\:=\:{sin}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}={tan}^{−\mathrm{1}} \sqrt{\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}}={cos}^{−\mathrm{1}} \sqrt{\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}} \\ $$$${m}_{\mathrm{1}} =\:{sec}^{\mathrm{2}} \left({cos}^{−\mathrm{1}} \sqrt{\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}}\right)=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}−\mathrm{1}}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}} \\ $$$${m}_{\mathrm{2}} =\:−{sin}\left({sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)=−\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}} \\ $$$$\because\:{m}_{\mathrm{1}} \centerdot{m}_{\mathrm{2}} =−\mathrm{1} \\ $$$$\therefore\:\frac{{a}}{{b}}={m}_{\mathrm{1}} =\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}=\mathrm{1}.\mathrm{61803398}… \\ $$
Commented by M±th+et+s last updated on 26/Apr/20
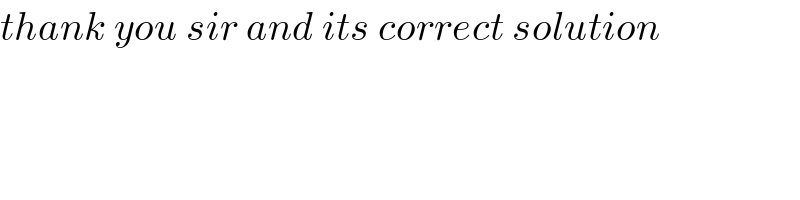
$${thank}\:{you}\:{sir}\:{and}\:{its}\:{correct}\:{solution} \\ $$
