Question Number 90989 by ajfour last updated on 27/Apr/20

Commented by ajfour last updated on 27/Apr/20

$${If}\:{eq}.\:{of}\:{parabola}\:{is}\:\:\mathrm{9}{y}=\mathrm{4}\left({x}^{\mathrm{2}} −\mathrm{9}\right) \\ $$$${and}\:{AB}={BC}={CD},\:{find}\:{eq}.\:{of} \\ $$$${the}\:{line}\:{AD}. \\ $$
Answered by mr W last updated on 27/Apr/20
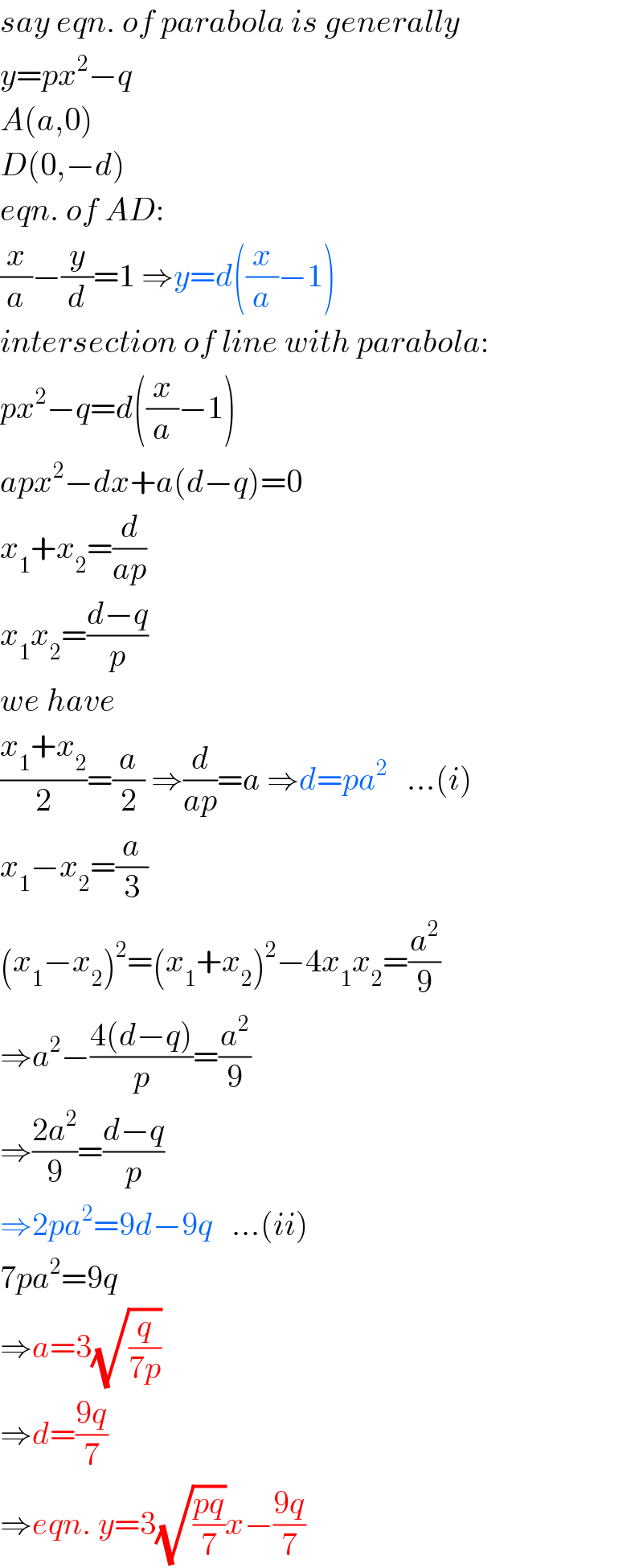
$${say}\:{eqn}.\:{of}\:{parabola}\:{is}\:{generally} \\ $$$${y}={px}^{\mathrm{2}} −{q} \\ $$$${A}\left({a},\mathrm{0}\right) \\ $$$${D}\left(\mathrm{0},−{d}\right) \\ $$$${eqn}.\:{of}\:{AD}: \\ $$$$\frac{{x}}{{a}}−\frac{{y}}{{d}}=\mathrm{1}\:\Rightarrow{y}={d}\left(\frac{{x}}{{a}}−\mathrm{1}\right) \\ $$$${intersection}\:{of}\:{line}\:{with}\:{parabola}: \\ $$$${px}^{\mathrm{2}} −{q}={d}\left(\frac{{x}}{{a}}−\mathrm{1}\right) \\ $$$${apx}^{\mathrm{2}} −{dx}+{a}\left({d}−{q}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} =\frac{{d}}{{ap}} \\ $$$${x}_{\mathrm{1}} {x}_{\mathrm{2}} =\frac{{d}−{q}}{{p}} \\ $$$${we}\:{have} \\ $$$$\frac{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} }{\mathrm{2}}=\frac{{a}}{\mathrm{2}}\:\Rightarrow\frac{{d}}{{ap}}={a}\:\Rightarrow{d}={pa}^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$${x}_{\mathrm{1}} −{x}_{\mathrm{2}} =\frac{{a}}{\mathrm{3}}\: \\ $$$$\left({x}_{\mathrm{1}} −{x}_{\mathrm{2}} \right)^{\mathrm{2}} =\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{x}_{\mathrm{1}} {x}_{\mathrm{2}} =\frac{{a}^{\mathrm{2}} }{\mathrm{9}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} −\frac{\mathrm{4}\left({d}−{q}\right)}{{p}}=\frac{{a}^{\mathrm{2}} }{\mathrm{9}} \\ $$$$\Rightarrow\frac{\mathrm{2}{a}^{\mathrm{2}} }{\mathrm{9}}=\frac{{d}−{q}}{{p}} \\ $$$$\Rightarrow\mathrm{2}{pa}^{\mathrm{2}} =\mathrm{9}{d}−\mathrm{9}{q}\:\:\:…\left({ii}\right) \\ $$$$\mathrm{7}{pa}^{\mathrm{2}} =\mathrm{9}{q} \\ $$$$\Rightarrow{a}=\mathrm{3}\sqrt{\frac{{q}}{\mathrm{7}{p}}} \\ $$$$\Rightarrow{d}=\frac{\mathrm{9}{q}}{\mathrm{7}} \\ $$$$\Rightarrow{eqn}.\:{y}=\mathrm{3}\sqrt{\frac{{pq}}{\mathrm{7}}}{x}−\frac{\mathrm{9}{q}}{\mathrm{7}} \\ $$
Commented by ajfour last updated on 27/Apr/20

$${Thanks}\:{Sir},\:{too}\:{good}\:{and}\:{great}, \\ $$$${you}\:{solved}\:{it}\:{generally}! \\ $$
Commented by mr W last updated on 27/Apr/20

