Question Number 91054 by Mikael_786 last updated on 27/Apr/20

Commented by MJS last updated on 27/Apr/20
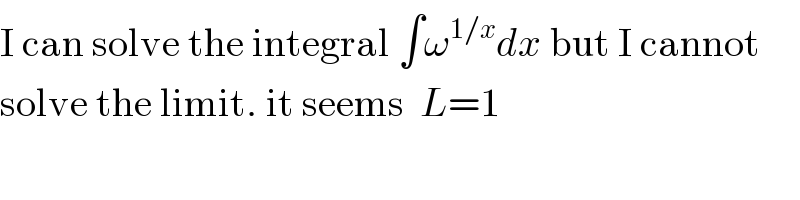
$$\mathrm{I}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{integral}\:\int\omega^{\mathrm{1}/{x}} {dx}\:\mathrm{but}\:\mathrm{I}\:\mathrm{cannot} \\ $$$$\mathrm{solve}\:\mathrm{the}\:\mathrm{limit}.\:\mathrm{it}\:\mathrm{seems}\:\:{L}=\mathrm{1} \\ $$
Commented by MJS last updated on 28/Apr/20
![∫ω^(1/x) dx= [by parts] =ω^(1/x) x+ln ω ∫(ω^(1/x) /x)dx= ∫(ω^(1/x) /x)dx= [t=(1/x) → dx=−x^2 dt] =−∫(ω^t /t)dt=Ei (tln ω) =Ei ((ln ω)/x) =ω^(1/x) x−ln ω Ei ((ln ω)/x) +C (1/ω)∫_1 ^ω ω^(1/x) dx=(1/ω)[ω^(1/x) x−ln ω Ei ((ln ω)/x)]_1 ^ω = =(1/ω)(ω^(1/ω+1) −ω−ln ω Ei ((ln ω)/ω) +ln ω Ei ln ω) =ω^(1/ω) −1+((ln ω)/ω)(Ei ln ω −Ei ((ln ω)/ω)) lim_(ω→∞) ω^(1/ω) −1 =0 lim_(ω→∞) ((ln ω)/ω)(Ei ln ω −Ei ((ln ω)/ω)) =? my knowledge ends here](https://www.tinkutara.com/question/Q91214.png)
$$\int\omega^{\mathrm{1}/{x}} {dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{by}\:\mathrm{parts}\right] \\ $$$$=\omega^{\mathrm{1}/{x}} {x}+\mathrm{ln}\:\omega\:\int\frac{\omega^{\mathrm{1}/{x}} }{{x}}{dx}= \\ $$$$ \\ $$$$\:\:\:\:\:\int\frac{\omega^{\mathrm{1}/{x}} }{{x}}{dx}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{t}=\frac{\mathrm{1}}{{x}}\:\rightarrow\:{dx}=−{x}^{\mathrm{2}} {dt}\right] \\ $$$$\:\:\:\:\:=−\int\frac{\omega^{{t}} }{{t}}{dt}=\mathrm{Ei}\:\left({t}\mathrm{ln}\:\omega\right)\:=\mathrm{Ei}\:\frac{\mathrm{ln}\:\omega}{{x}} \\ $$$$ \\ $$$$=\omega^{\mathrm{1}/{x}} {x}−\mathrm{ln}\:\omega\:\mathrm{Ei}\:\frac{\mathrm{ln}\:\omega}{{x}}\:+{C} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\omega}\underset{\mathrm{1}} {\overset{\omega} {\int}}\omega^{\mathrm{1}/{x}} {dx}=\frac{\mathrm{1}}{\omega}\left[\omega^{\mathrm{1}/{x}} {x}−\mathrm{ln}\:\omega\:\mathrm{Ei}\:\frac{\mathrm{ln}\:\omega}{{x}}\right]_{\mathrm{1}} ^{\omega} = \\ $$$$=\frac{\mathrm{1}}{\omega}\left(\omega^{\mathrm{1}/\omega+\mathrm{1}} −\omega−\mathrm{ln}\:\omega\:\mathrm{Ei}\:\frac{\mathrm{ln}\:\omega}{\omega}\:+\mathrm{ln}\:\omega\:\mathrm{Ei}\:\mathrm{ln}\:\omega\right) \\ $$$$=\omega^{\frac{\mathrm{1}}{\omega}} −\mathrm{1}+\frac{\mathrm{ln}\:\omega}{\omega}\left(\mathrm{Ei}\:\mathrm{ln}\:\omega\:−\mathrm{Ei}\:\frac{\mathrm{ln}\:\omega}{\omega}\right) \\ $$$$\underset{\omega\rightarrow\infty} {\mathrm{lim}}\:\omega^{\frac{\mathrm{1}}{\omega}} −\mathrm{1}\:=\mathrm{0} \\ $$$$\underset{\omega\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\omega}{\omega}\left(\mathrm{Ei}\:\mathrm{ln}\:\omega\:−\mathrm{Ei}\:\frac{\mathrm{ln}\:\omega}{\omega}\right)\:=? \\ $$$$\mathrm{my}\:\mathrm{knowledge}\:\mathrm{ends}\:\mathrm{here} \\ $$
Answered by ~blr237~ last updated on 28/Apr/20
![assuming that w→∞ ,w≥1 ⇒ w>0 let state t=w^(1/x) then x=(1/(log_w (t)))=((lnw)/(lnt)) f(w)=∫_1 ^w w^(1/x) dx=∫_w ^w^(1/w) td(((lnw)/(lnt))) by part f(w)=lnw([(t/(lnt))]_w ^w^(1/w) −∫_w ^w^(1/w) (dt/(lnt))) f(w)=lnw([(w^(1/w) /((lnw)/w)) −(w/(lnw))]−li(w^(1/w) )+li(w)) f(w)=w^((1/w)+1) −w−li(w^(1/w) )lnw+li(w)lnw (1/w)f(w)= w^(1/w) −1−li(w^(1/w) )((lnw)/w) + li(w)((lnw)/w) we have lim_(w→∞) w^(1/w) =1 and lim_(w→∞) li(w)((lnw)/w)=1 Sir mrW assuming your answer is correct How can we prove that lim_(w→∞) li(w^(1/w) )((lnw)/w) =0 knowing that lim_(x→1) li(x)=−∞ with li(x)=∫_0 ^x (dt/(lnt)) can we prove that lim_(x→1) li(x)ln(x)=0 ??](https://www.tinkutara.com/question/Q91150.png)
$${assuming}\:{that}\:\:{w}\rightarrow\infty\:,{w}\geqslant\mathrm{1}\:\Rightarrow\:{w}>\mathrm{0} \\ $$$${let}\:{state}\:\:\:{t}={w}^{\frac{\mathrm{1}}{{x}}} \:\:{then}\:\:{x}=\frac{\mathrm{1}}{{log}_{{w}} \left({t}\right)}=\frac{{lnw}}{{lnt}}\: \\ $$$${f}\left({w}\right)=\int_{\mathrm{1}} ^{{w}} {w}^{\frac{\mathrm{1}}{{x}}} {dx}=\int_{{w}} ^{{w}^{\frac{\mathrm{1}}{{w}}} } {td}\left(\frac{{lnw}}{{lnt}}\right)\: \\ $$$${by}\:{part}\:{f}\left({w}\right)={lnw}\left(\left[\frac{{t}}{{lnt}}\right]_{{w}} ^{{w}^{\frac{\mathrm{1}}{{w}}} } −\int_{{w}} ^{{w}^{\frac{\mathrm{1}}{{w}}} } \frac{{dt}}{{lnt}}\right) \\ $$$${f}\left({w}\right)={lnw}\left(\left[\frac{{w}^{\frac{\mathrm{1}}{{w}}} }{\frac{{lnw}}{{w}}}\:−\frac{{w}}{{lnw}}\right]−{li}\left({w}^{\frac{\mathrm{1}}{{w}}} \right)+{li}\left({w}\right)\right) \\ $$$${f}\left({w}\right)={w}^{\frac{\mathrm{1}}{{w}}+\mathrm{1}} −{w}−{li}\left({w}^{\frac{\mathrm{1}}{{w}}} \right){lnw}+{li}\left({w}\right){lnw} \\ $$$$\frac{\mathrm{1}}{{w}}{f}\left({w}\right)=\:{w}^{\frac{\mathrm{1}}{{w}}} −\mathrm{1}−{li}\left({w}^{\frac{\mathrm{1}}{{w}}} \right)\frac{{lnw}}{{w}}\:+\:{li}\left({w}\right)\frac{{lnw}}{{w}}\: \\ $$$${we}\:{have}\:\:\underset{{w}\rightarrow\infty} {\mathrm{lim}}\:{w}^{\frac{\mathrm{1}}{{w}}} =\mathrm{1}\:\:\:{and}\:\:\underset{{w}\rightarrow\infty} {\mathrm{lim}}\:{li}\left({w}\right)\frac{{lnw}}{{w}}=\mathrm{1}\:\: \\ $$$${Sir}\:{mrW}\:\:\:{assuming}\:{your}\:{answer}\:{is}\:{correct}\: \\ $$$${How}\:{can}\:{we}\:{prove}\:{that}\:\:\:\underset{{w}\rightarrow\infty} {\mathrm{lim}}\:{li}\left({w}^{\frac{\mathrm{1}}{{w}}} \right)\frac{{lnw}}{{w}}\:=\mathrm{0} \\ $$$${knowing}\:\:{that}\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:{li}\left({x}\right)=−\infty\:\:{with}\:{li}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \frac{{dt}}{{lnt}}\: \\ $$$$\: \\ $$$${can}\:{we}\:{prove}\:{that}\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:{li}\left({x}\right){ln}\left({x}\right)=\mathrm{0}\:?? \\ $$$$ \\ $$
