Menu Close

Question-91099

Tinku Tara 0 Comments
Pin




Question Number 91099 by Angnysr11 last updated on 28/Apr/20
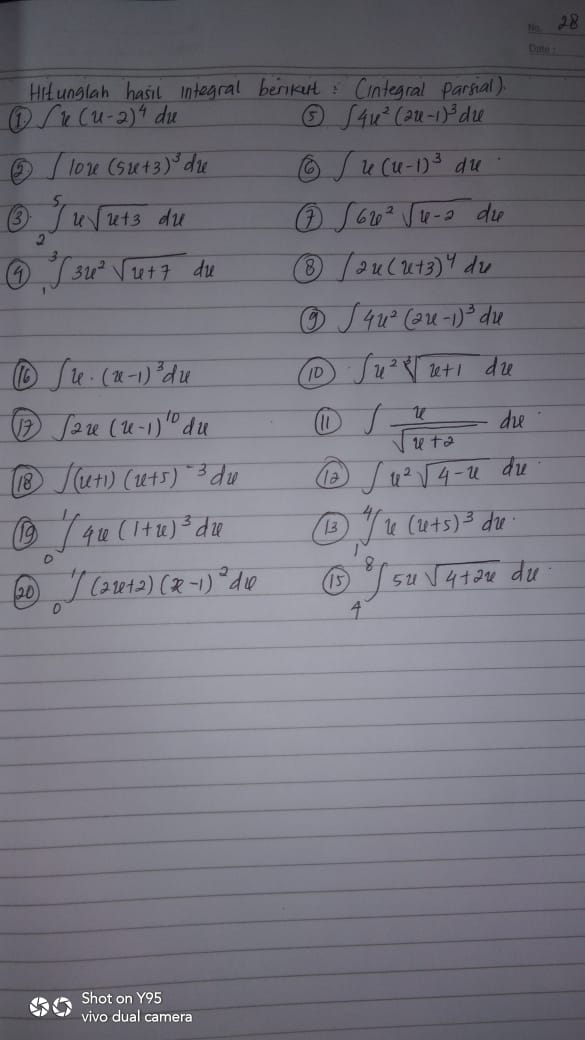
Commented by Angnysr11 last updated on 28/Apr/20
i determinant (( [((i can′t solve this... please help)),() ]),())
$${i}\begin{vmatrix}{\begin{bmatrix}{{i}\:{can}'{t}\:{solve}\:{this}…\:{please}\:{help}}\\{}\end{bmatrix}}\\{}\end{vmatrix} \\ $$
Commented by john santu last updated on 28/Apr/20
15) ∫_4 ^8 5u(√(4+2u)) du = (√(4+2u)) = w ⇒ 2du = 2w dw ∫^(2(√5)) _(2(√3)) 5(((w^2 −4)/2)).w wdw = (5/2)∫_(2(√3)) ^(2(√5)) (w^4 −4w^2 )dw = (5/2)[(1/5)w^5 −(4/3)w^3 ]_(2(√3)) ^(2(√5)) now it easy to solve
$$\left.\mathrm{15}\right)\:\underset{\mathrm{4}} {\overset{\mathrm{8}} {\int}}\:\mathrm{5}{u}\sqrt{\mathrm{4}+\mathrm{2}{u}}\:{du}\:= \\ $$$$\sqrt{\mathrm{4}+\mathrm{2}{u}}\:=\:{w}\:\Rightarrow\:\mathrm{2}{du}\:=\:\mathrm{2}{w}\:{dw}\: \\ $$$$\underset{\mathrm{2}\sqrt{\mathrm{3}}} {\int}^{\mathrm{2}\sqrt{\mathrm{5}}} \mathrm{5}\left(\frac{{w}^{\mathrm{2}} −\mathrm{4}}{\mathrm{2}}\right).{w}\:{wdw}\:=\: \\ $$$$\frac{\mathrm{5}}{\mathrm{2}}\int_{\mathrm{2}\sqrt{\mathrm{3}}} ^{\mathrm{2}\sqrt{\mathrm{5}}} \left({w}^{\mathrm{4}} −\mathrm{4}{w}^{\mathrm{2}} \right){dw}\:= \\ $$$$\frac{\mathrm{5}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{5}}{w}^{\mathrm{5}} −\frac{\mathrm{4}}{\mathrm{3}}{w}^{\mathrm{3}} \:\right]_{\mathrm{2}\sqrt{\mathrm{3}}} ^{\mathrm{2}\sqrt{\mathrm{5}}} \\ $$$${now}\:{it}\:{easy}\:\:{to}\:{solve} \\ $$
Commented by abdomathmax last updated on 28/Apr/20
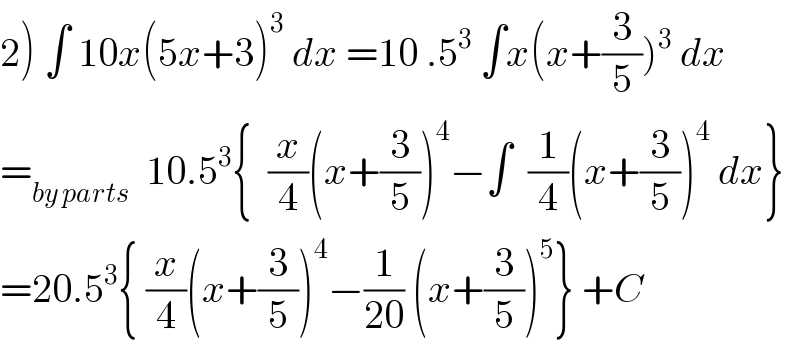
2) ∫ 10x(5x+3)^3 dx =10 .5^3 ∫x(x+(3/5))^3 dx =_(by parts) 10.5^3 { (x/4)(x+(3/5))^4 −∫ (1/4)(x+(3/5))^4 dx} =20.5^3 { (x/4)(x+(3/5))^4 −(1/(20)) (x+(3/5))^5 } +C
$$\left.\mathrm{2}\right)\:\int\:\mathrm{10}{x}\left(\mathrm{5}{x}+\mathrm{3}\right)^{\mathrm{3}} \:{dx}\:=\mathrm{10}\:.\mathrm{5}^{\mathrm{3}} \:\int{x}\left({x}+\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{3}} \:{dx} \\ $$$$=_{{by}\:{parts}} \:\:\mathrm{10}.\mathrm{5}^{\mathrm{3}} \left\{\:\:\frac{{x}}{\mathrm{4}}\left({x}+\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{4}} −\int\:\:\frac{\mathrm{1}}{\mathrm{4}}\left({x}+\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{4}} \:{dx}\right\} \\ $$$$=\mathrm{20}.\mathrm{5}^{\mathrm{3}} \left\{\:\frac{{x}}{\mathrm{4}}\left({x}+\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{4}} −\frac{\mathrm{1}}{\mathrm{20}}\:\left({x}+\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{5}} \right\}\:+{C} \\ $$
Commented by abdomathmax last updated on 28/Apr/20
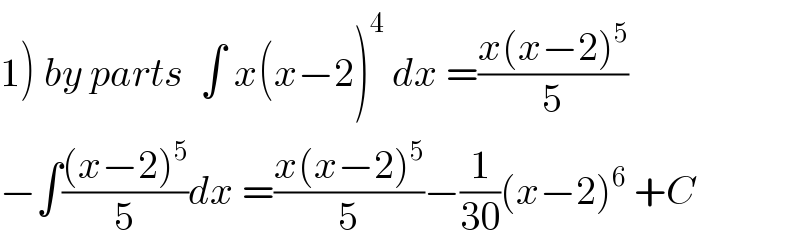
1) by parts ∫ x(x−2)^4 dx =((x(x−2)^5 )/5) −∫(((x−2)^5 )/5)dx =((x(x−2)^5 )/5)−(1/(30))(x−2)^6 +C
$$\left.\mathrm{1}\right)\:{by}\:{parts}\:\:\int\:{x}\left({x}−\mathrm{2}\right)^{\mathrm{4}} \:{dx}\:=\frac{{x}\left({x}−\mathrm{2}\right)^{\mathrm{5}} }{\mathrm{5}} \\ $$$$−\int\frac{\left({x}−\mathrm{2}\right)^{\mathrm{5}} }{\mathrm{5}}{dx}\:=\frac{{x}\left({x}−\mathrm{2}\right)^{\mathrm{5}} }{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{30}}\left({x}−\mathrm{2}\right)^{\mathrm{6}} \:+{C} \\ $$
Commented by abdomathmax last updated on 28/Apr/20
3) ∫_2 ^5 x(√(x+3))dx =_((√(x+3))=t) ∫_(√5) ^(2(√2)) (t^2 −3)t (2t)dt =2 ∫_(√5) ^(2(√2)) (t^4 −3t^2 )dt =2[(t^5 /5)−t^3 ]_(√5) ^(2(√2)) =2((((2(√2))^5 )/5)−(2(√2))^3 −((((√5))^5 )/5) +((√5))^3 )
$$\left.\mathrm{3}\right)\:\int_{\mathrm{2}} ^{\mathrm{5}} {x}\sqrt{{x}+\mathrm{3}}{dx}\:\:=_{\sqrt{{x}+\mathrm{3}}={t}} \:\:\int_{\sqrt{\mathrm{5}}} ^{\mathrm{2}\sqrt{\mathrm{2}}} \left({t}^{\mathrm{2}} −\mathrm{3}\right){t}\:\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\:\int_{\sqrt{\mathrm{5}}} ^{\mathrm{2}\sqrt{\mathrm{2}}} \left({t}^{\mathrm{4}} −\mathrm{3}{t}^{\mathrm{2}} \right){dt}\:=\mathrm{2}\left[\frac{{t}^{\mathrm{5}} }{\mathrm{5}}−{t}^{\mathrm{3}} \right]_{\sqrt{\mathrm{5}}} ^{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$=\mathrm{2}\left(\frac{\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{5}} }{\mathrm{5}}−\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{3}} −\frac{\left(\sqrt{\mathrm{5}}\right)^{\mathrm{5}} }{\mathrm{5}}\:+\left(\sqrt{\mathrm{5}}\right)^{\mathrm{3}} \right) \\ $$
Commented by abdomathmax last updated on 28/Apr/20
4) ∫_1 ^3 3x^2 (√(x+7))dx =_(.(√(x+7))=t) ∫_(2(√2)) ^(√(10)) 3(t^2 −7)^2 t(2t)dt =6 ∫_(2(√2)) ^(√(10)) t^2 (t^4 −14t^2 +49)dt =6 ∫_(2(√2)) ^(√(10)) (t^6 −14t^4 +49t^2 )dt =6[(t^7 /7)−((14)/5)t^5 +((49)/3)t^3 ]_(2(√2)) ^(√(10)) =6( ((((√(10)))^7 )/7)−((14)/5)((√(10)))^5 +((49)/3)((√(10)))^3 −(((2(√2))^7 )/7)+((14)/5)(2(√2))^5 −((49)/3)(2(√2))^3 )
$$\left.\mathrm{4}\right)\:\int_{\mathrm{1}} ^{\mathrm{3}} \:\mathrm{3}{x}^{\mathrm{2}} \sqrt{{x}+\mathrm{7}}{dx}\:=_{.\sqrt{{x}+\mathrm{7}}={t}} \:\:\int_{\mathrm{2}\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{10}}} \mathrm{3}\left({t}^{\mathrm{2}} −\mathrm{7}\right)^{\mathrm{2}} {t}\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{6}\:\int_{\mathrm{2}\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{10}}} {t}^{\mathrm{2}} \left({t}^{\mathrm{4}} −\mathrm{14}{t}^{\mathrm{2}} +\mathrm{49}\right){dt} \\ $$$$=\mathrm{6}\:\int_{\mathrm{2}\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{10}}} \left({t}^{\mathrm{6}} −\mathrm{14}{t}^{\mathrm{4}} \:+\mathrm{49}{t}^{\mathrm{2}} \right){dt} \\ $$$$=\mathrm{6}\left[\frac{{t}^{\mathrm{7}} }{\mathrm{7}}−\frac{\mathrm{14}}{\mathrm{5}}{t}^{\mathrm{5}} \:+\frac{\mathrm{49}}{\mathrm{3}}{t}^{\mathrm{3}} \right]_{\mathrm{2}\sqrt{\mathrm{2}}} ^{\sqrt{\mathrm{10}}} \\ $$$$=\mathrm{6}\left(\:\frac{\left(\sqrt{\mathrm{10}}\right)^{\mathrm{7}} }{\mathrm{7}}−\frac{\mathrm{14}}{\mathrm{5}}\left(\sqrt{\mathrm{10}}\right)^{\mathrm{5}} \:+\frac{\mathrm{49}}{\mathrm{3}}\left(\sqrt{\mathrm{10}}\right)^{\mathrm{3}} −\frac{\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{7}} }{\mathrm{7}}+\frac{\mathrm{14}}{\mathrm{5}}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{5}} \right. \\ $$$$\left.−\frac{\mathrm{49}}{\mathrm{3}}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{3}} \right) \\ $$
Commented by abdomathmax last updated on 28/Apr/20
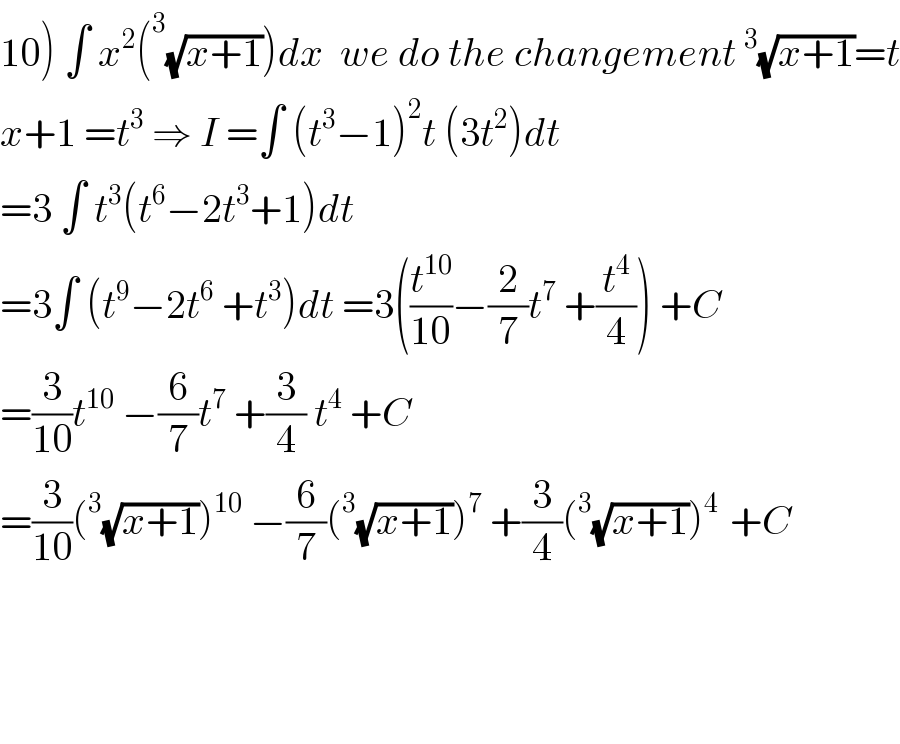
10) ∫ x^2 (^3 (√(x+1)))dx we do the changement^3 (√(x+1))=t x+1 =t^3 ⇒ I =∫ (t^3 −1)^2 t (3t^2 )dt =3 ∫ t^3 (t^6 −2t^3 +1)dt =3∫ (t^9 −2t^6 +t^3 )dt =3((t^(10) /(10))−(2/7)t^7 +(t^4 /4)) +C =(3/(10))t^(10) −(6/7)t^7 +(3/4) t^4 +C =(3/(10))(^3 (√(x+1)))^(10) −(6/7)(^3 (√(x+1)))^7 +(3/4)(^3 (√(x+1)))^(4 ) +C
$$\left.\mathrm{10}\right)\:\int\:{x}^{\mathrm{2}} \left(^{\mathrm{3}} \sqrt{{x}+\mathrm{1}}\right){dx}\:\:{we}\:{do}\:{the}\:{changement}\:^{\mathrm{3}} \sqrt{{x}+\mathrm{1}}={t} \\ $$$${x}+\mathrm{1}\:={t}^{\mathrm{3}} \:\Rightarrow\:{I}\:=\int\:\left({t}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} {t}\:\left(\mathrm{3}{t}^{\mathrm{2}} \right){dt} \\ $$$$=\mathrm{3}\:\int\:{t}^{\mathrm{3}} \left({t}^{\mathrm{6}} −\mathrm{2}{t}^{\mathrm{3}} +\mathrm{1}\right){dt} \\ $$$$=\mathrm{3}\int\:\left({t}^{\mathrm{9}} −\mathrm{2}{t}^{\mathrm{6}} \:+{t}^{\mathrm{3}} \right){dt}\:=\mathrm{3}\left(\frac{{t}^{\mathrm{10}} }{\mathrm{10}}−\frac{\mathrm{2}}{\mathrm{7}}{t}^{\mathrm{7}} \:+\frac{{t}^{\mathrm{4}} }{\mathrm{4}}\right)\:+{C} \\ $$$$=\frac{\mathrm{3}}{\mathrm{10}}{t}^{\mathrm{10}} \:−\frac{\mathrm{6}}{\mathrm{7}}{t}^{\mathrm{7}} \:+\frac{\mathrm{3}}{\mathrm{4}}\:{t}^{\mathrm{4}} \:+{C} \\ $$$$=\frac{\mathrm{3}}{\mathrm{10}}\left(^{\mathrm{3}} \sqrt{{x}+\mathrm{1}}\right)^{\mathrm{10}} \:−\frac{\mathrm{6}}{\mathrm{7}}\left(^{\mathrm{3}} \sqrt{{x}+\mathrm{1}}\right)^{\mathrm{7}} \:+\frac{\mathrm{3}}{\mathrm{4}}\left(^{\mathrm{3}} \sqrt{{x}+\mathrm{1}}\right)^{\mathrm{4}\:} \:+{C} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by abdomathmax last updated on 28/Apr/20
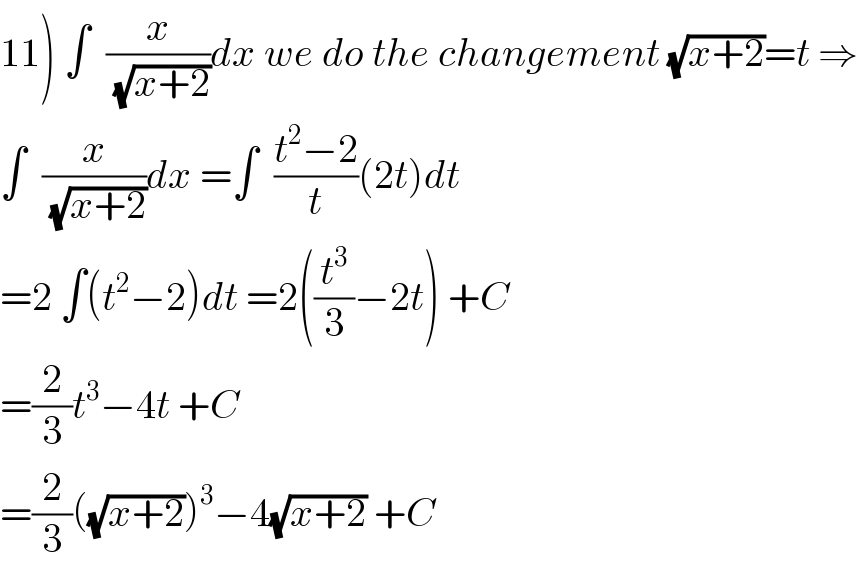
11) ∫ (x/( (√(x+2))))dx we do the changement (√(x+2))=t ⇒ ∫ (x/( (√(x+2))))dx =∫ ((t^2 −2)/t)(2t)dt =2 ∫(t^2 −2)dt =2((t^3 /3)−2t) +C =(2/3)t^3 −4t +C =(2/3)((√(x+2)))^3 −4(√(x+2)) +C
$$\left.\mathrm{11}\right)\:\int\:\:\frac{{x}}{\:\sqrt{{x}+\mathrm{2}}}{dx}\:{we}\:{do}\:{the}\:{changement}\:\sqrt{{x}+\mathrm{2}}={t}\:\Rightarrow \\ $$$$\int\:\:\frac{{x}}{\:\sqrt{{x}+\mathrm{2}}}{dx}\:=\int\:\:\frac{{t}^{\mathrm{2}} −\mathrm{2}}{{t}}\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\:\int\left({t}^{\mathrm{2}} −\mathrm{2}\right){dt}\:=\mathrm{2}\left(\frac{{t}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{2}{t}\right)\:+{C} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}{t}^{\mathrm{3}} −\mathrm{4}{t}\:+{C} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\left(\sqrt{{x}+\mathrm{2}}\right)^{\mathrm{3}} −\mathrm{4}\sqrt{{x}+\mathrm{2}}\:+{C} \\ $$
Commented by abdomathmax last updated on 28/Apr/20
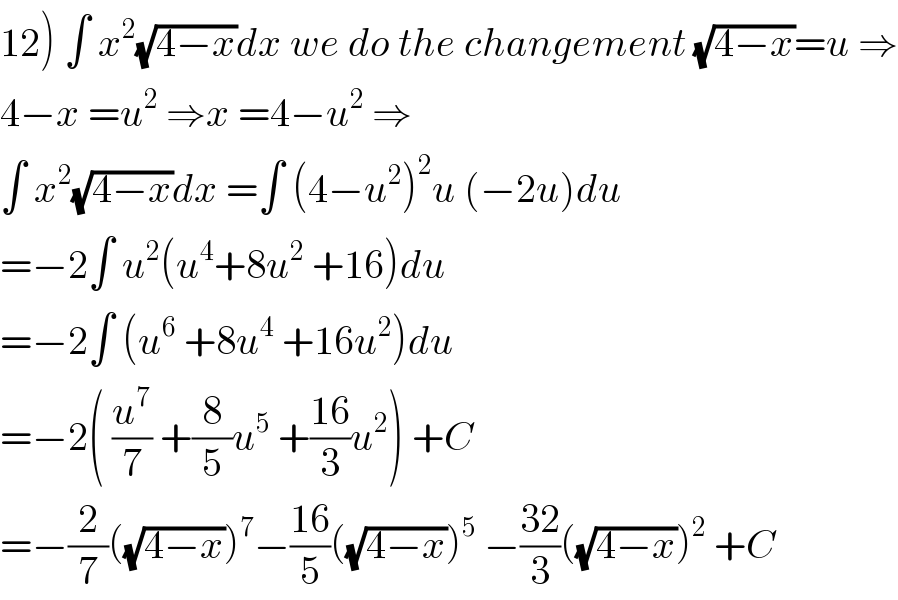
12) ∫ x^2 (√(4−x))dx we do the changement (√(4−x))=u ⇒ 4−x =u^2 ⇒x =4−u^2 ⇒ ∫ x^2 (√(4−x))dx =∫ (4−u^2 )^2 u (−2u)du =−2∫ u^2 (u^4 +8u^2 +16)du =−2∫ (u^6 +8u^4 +16u^2 )du =−2( (u^7 /7) +(8/5)u^5 +((16)/3)u^2 ) +C =−(2/7)((√(4−x)))^7 −((16)/5)((√(4−x)))^5 −((32)/3)((√(4−x)))^2 +C
$$\left.\mathrm{12}\right)\:\int\:{x}^{\mathrm{2}} \sqrt{\mathrm{4}−{x}}{dx}\:{we}\:{do}\:{the}\:{changement}\:\sqrt{\mathrm{4}−{x}}={u}\:\Rightarrow \\ $$$$\mathrm{4}−{x}\:={u}^{\mathrm{2}} \:\Rightarrow{x}\:=\mathrm{4}−{u}^{\mathrm{2}} \:\Rightarrow \\ $$$$\int\:{x}^{\mathrm{2}} \sqrt{\mathrm{4}−{x}}{dx}\:=\int\:\left(\mathrm{4}−{u}^{\mathrm{2}} \right)^{\mathrm{2}} {u}\:\left(−\mathrm{2}{u}\right){du} \\ $$$$=−\mathrm{2}\int\:{u}^{\mathrm{2}} \left({u}^{\mathrm{4}} +\mathrm{8}{u}^{\mathrm{2}} \:+\mathrm{16}\right){du} \\ $$$$=−\mathrm{2}\int\:\left({u}^{\mathrm{6}} \:+\mathrm{8}{u}^{\mathrm{4}} \:+\mathrm{16}{u}^{\mathrm{2}} \right){du} \\ $$$$=−\mathrm{2}\left(\:\frac{{u}^{\mathrm{7}} }{\mathrm{7}}\:+\frac{\mathrm{8}}{\mathrm{5}}{u}^{\mathrm{5}} \:+\frac{\mathrm{16}}{\mathrm{3}}{u}^{\mathrm{2}} \right)\:+{C} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{7}}\left(\sqrt{\mathrm{4}−{x}}\right)^{\mathrm{7}} −\frac{\mathrm{16}}{\mathrm{5}}\left(\sqrt{\mathrm{4}−{x}}\right)^{\mathrm{5}} \:−\frac{\mathrm{32}}{\mathrm{3}}\left(\sqrt{\mathrm{4}−{x}}\right)^{\mathrm{2}} \:+{C} \\ $$
Commented by mathmax by abdo last updated on 28/Apr/20
13) ∫_1 ^4 x(x+5)^3 dx =_(by parts) [(x/4)(x+5)^4 ]_1 ^4 −∫_1 ^4 (1/4)(x+5)^4 dx =9^4 −(6^4 /4)−(1/(20))[(x+5)^5 ]_1 ^4 =9^4 −(6^4 /4)−(1/(20))( 9^5 −6^5 )
$$\left.\mathrm{13}\right)\:\int_{\mathrm{1}} ^{\mathrm{4}} {x}\left({x}+\mathrm{5}\right)^{\mathrm{3}} {dx}\:=_{{by}\:{parts}} \:\:\left[\frac{{x}}{\mathrm{4}}\left({x}+\mathrm{5}\right)^{\mathrm{4}} \right]_{\mathrm{1}} ^{\mathrm{4}} −\int_{\mathrm{1}} ^{\mathrm{4}} \frac{\mathrm{1}}{\mathrm{4}}\left({x}+\mathrm{5}\right)^{\mathrm{4}} \:{dx} \\ $$$$=\mathrm{9}^{\mathrm{4}} −\frac{\mathrm{6}^{\mathrm{4}} }{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{20}}\left[\left({x}+\mathrm{5}\right)^{\mathrm{5}} \right]_{\mathrm{1}} ^{\mathrm{4}} \:=\mathrm{9}^{\mathrm{4}} −\frac{\mathrm{6}^{\mathrm{4}} }{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{20}}\left(\:\mathrm{9}^{\mathrm{5}} −\mathrm{6}^{\mathrm{5}} \right) \\ $$
Commented by mathmax by abdo last updated on 28/Apr/20
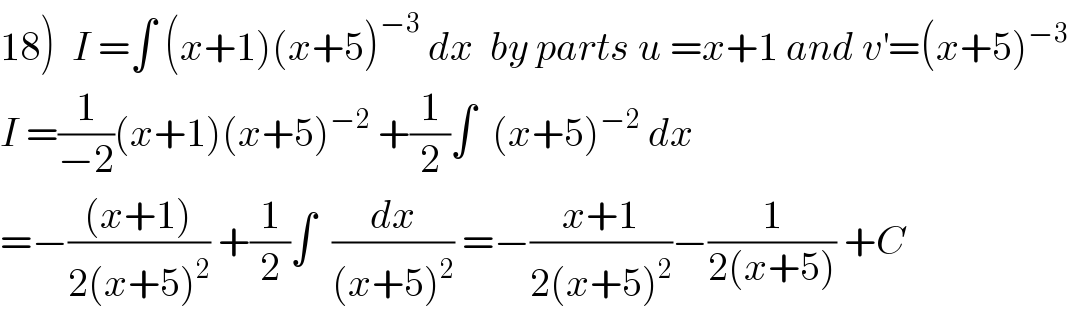
18) I =∫ (x+1)(x+5)^(−3) dx by parts u =x+1 and v^′ =(x+5)^(−3) I =(1/(−2))(x+1)(x+5)^(−2) +(1/2)∫ (x+5)^(−2) dx =−(((x+1))/(2(x+5)^2 )) +(1/2)∫ (dx/((x+5)^2 )) =−((x+1)/(2(x+5)^2 ))−(1/(2(x+5))) +C
$$\left.\mathrm{18}\right)\:\:{I}\:=\int\:\left({x}+\mathrm{1}\right)\left({x}+\mathrm{5}\right)^{−\mathrm{3}} \:{dx}\:\:{by}\:{parts}\:{u}\:={x}+\mathrm{1}\:{and}\:{v}^{'} =\left({x}+\mathrm{5}\right)^{−\mathrm{3}} \\ $$$${I}\:=\frac{\mathrm{1}}{−\mathrm{2}}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{5}\right)^{−\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\left({x}+\mathrm{5}\right)^{−\mathrm{2}} \:{dx} \\ $$$$=−\frac{\left({x}+\mathrm{1}\right)}{\mathrm{2}\left({x}+\mathrm{5}\right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{{dx}}{\left({x}+\mathrm{5}\right)^{\mathrm{2}} }\:=−\frac{{x}+\mathrm{1}}{\mathrm{2}\left({x}+\mathrm{5}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}\left({x}+\mathrm{5}\right)}\:+{C} \\ $$
Commented by mathmax by abdo last updated on 28/Apr/20
15) I =∫_4 ^8 5x(√(4+2x))dx we do the changement (√(4+2x))=t ⇒ 4+2x =t^2 ⇒2x =t^2 −4 ⇒x =(t^2 /2)−2 ⇒ I =5 ∫_(2(√3)) ^(2(√5)) ((t^2 /2)−2)t (t)dt =5 ∫_(2(√3)) ^(2(√5)) ((t^4 /2)−2t^2 )dt =5[(1/(10))t^5 −(2/3)t^3 ]_(2(√3)) ^(2(√5)) =5( (((2(√5))^5 )/(10))−(2/3)(2(√5))^3 −(((2(√3))^5 )/(10))+(2/3)(2(√3))^3 )
$$\left.\mathrm{15}\right)\:{I}\:=\int_{\mathrm{4}} ^{\mathrm{8}} \:\mathrm{5}{x}\sqrt{\mathrm{4}+\mathrm{2}{x}}{dx}\:\:{we}\:{do}\:{the}\:{changement}\:\sqrt{\mathrm{4}+\mathrm{2}{x}}={t}\:\Rightarrow \\ $$$$\mathrm{4}+\mathrm{2}{x}\:={t}^{\mathrm{2}} \:\Rightarrow\mathrm{2}{x}\:={t}^{\mathrm{2}} −\mathrm{4}\:\Rightarrow{x}\:=\frac{{t}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}\:\Rightarrow \\ $$$${I}\:=\mathrm{5}\:\int_{\mathrm{2}\sqrt{\mathrm{3}}} ^{\mathrm{2}\sqrt{\mathrm{5}}} \:\:\left(\frac{{t}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}\right){t}\:\left({t}\right){dt}\:=\mathrm{5}\:\int_{\mathrm{2}\sqrt{\mathrm{3}}} ^{\mathrm{2}\sqrt{\mathrm{5}}} \left(\frac{{t}^{\mathrm{4}} }{\mathrm{2}}−\mathrm{2}{t}^{\mathrm{2}} \right){dt} \\ $$$$=\mathrm{5}\left[\frac{\mathrm{1}}{\mathrm{10}}{t}^{\mathrm{5}} −\frac{\mathrm{2}}{\mathrm{3}}{t}^{\mathrm{3}} \right]_{\mathrm{2}\sqrt{\mathrm{3}}} ^{\mathrm{2}\sqrt{\mathrm{5}}} \:\:=\mathrm{5}\left(\:\:\frac{\left(\mathrm{2}\sqrt{\mathrm{5}}\right)^{\mathrm{5}} }{\mathrm{10}}−\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{2}\sqrt{\mathrm{5}}\right)^{\mathrm{3}} −\frac{\left(\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{5}} }{\mathrm{10}}+\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{3}} \right) \\ $$
Answered by Kunal12588 last updated on 28/Apr/20
1. ∫u(u−2)^4 du=∫(u−2)^5 du+2∫(u−2)^4 du = (1/6)(u−2)^6 +(2/5)(u−2)^5 +C 2. ∫10u(5u+3)^3 du=2∫(5u+3)^4 du−6∫(5u+3)^3 du =(2/(25))(5u+3)^5 −(3/(10))(5u+3)^4 +C 3. ∫_2 ^5 u(√(u+3)) du=∫_2 ^5 (u+3)^(3/2) du−3∫_2 ^5 (u+3)^(1/2) du =(2/5)[(u+3)^2 (√(u+3))]_2 ^5 −2[(u+3)(√(u+3))]_2 ^5 =(2/5)(128(√2)−25(√5))−2(16(√2)−5(√5)) =((96(√2))/5) 4. ∫_1 ^3 3u^2 (√(u+7)) du=∫_1 ^3 3((u+7)−7)^2 (√(u+7)) du =3[∫_1 ^3 (u+7)^(5/2) du−14∫_1 ^3 (u+7)^(3/2) du+49∫(u+7)^(1/2) du] =(6/7)[(u+7)^(7/2) ]_1 ^3 −((84)/5)[(u+7)^(5/2) ]_1 ^3 +49[(u+7)^(3/2) ]_1 ^3 =...
$$\mathrm{1}.\:\int{u}\left({u}−\mathrm{2}\right)^{\mathrm{4}} {du}=\int\left({u}−\mathrm{2}\right)^{\mathrm{5}} {du}+\mathrm{2}\int\left({u}−\mathrm{2}\right)^{\mathrm{4}} {du} \\ $$$$\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{6}}\left({u}−\mathrm{2}\right)^{\mathrm{6}} +\frac{\mathrm{2}}{\mathrm{5}}\left({u}−\mathrm{2}\right)^{\mathrm{5}} +{C} \\ $$$$\mathrm{2}.\:\int\mathrm{10}{u}\left(\mathrm{5}{u}+\mathrm{3}\right)^{\mathrm{3}} {du}=\mathrm{2}\int\left(\mathrm{5}{u}+\mathrm{3}\right)^{\mathrm{4}} {du}−\mathrm{6}\int\left(\mathrm{5}{u}+\mathrm{3}\right)^{\mathrm{3}} {du}\: \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{2}}{\mathrm{25}}\left(\mathrm{5}{u}+\mathrm{3}\right)^{\mathrm{5}} −\frac{\mathrm{3}}{\mathrm{10}}\left(\mathrm{5}{u}+\mathrm{3}\right)^{\mathrm{4}} +{C} \\ $$$$\mathrm{3}.\:\int_{\mathrm{2}} ^{\mathrm{5}} {u}\sqrt{{u}+\mathrm{3}}\:{du}=\int_{\mathrm{2}} ^{\mathrm{5}} \left({u}+\mathrm{3}\right)^{\mathrm{3}/\mathrm{2}} {du}−\mathrm{3}\int_{\mathrm{2}} ^{\mathrm{5}} \left({u}+\mathrm{3}\right)^{\mathrm{1}/\mathrm{2}} {du} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{2}}{\mathrm{5}}\left[\left({u}+\mathrm{3}\right)^{\mathrm{2}} \sqrt{{u}+\mathrm{3}}\right]_{\mathrm{2}} ^{\mathrm{5}} −\mathrm{2}\left[\left({u}+\mathrm{3}\right)\sqrt{{u}+\mathrm{3}}\right]_{\mathrm{2}} ^{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{2}}{\mathrm{5}}\left(\mathrm{128}\sqrt{\mathrm{2}}−\mathrm{25}\sqrt{\mathrm{5}}\right)−\mathrm{2}\left(\mathrm{16}\sqrt{\mathrm{2}}−\mathrm{5}\sqrt{\mathrm{5}}\right) \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{96}\sqrt{\mathrm{2}}}{\mathrm{5}} \\ $$$$\mathrm{4}.\:\int_{\mathrm{1}} ^{\mathrm{3}} \mathrm{3}{u}^{\mathrm{2}} \sqrt{{u}+\mathrm{7}}\:{du}=\int_{\mathrm{1}} ^{\mathrm{3}} \mathrm{3}\left(\left({u}+\mathrm{7}\right)−\mathrm{7}\right)^{\mathrm{2}} \sqrt{{u}+\mathrm{7}}\:{du} \\ $$$$=\mathrm{3}\left[\int_{\mathrm{1}} ^{\mathrm{3}} \left({u}+\mathrm{7}\right)^{\mathrm{5}/\mathrm{2}} {du}−\mathrm{14}\int_{\mathrm{1}} ^{\mathrm{3}} \left({u}+\mathrm{7}\right)^{\mathrm{3}/\mathrm{2}} {du}+\mathrm{49}\int\left({u}+\mathrm{7}\right)^{\mathrm{1}/\mathrm{2}} {du}\right] \\ $$$$=\frac{\mathrm{6}}{\mathrm{7}}\left[\left({u}+\mathrm{7}\right)^{\mathrm{7}/\mathrm{2}} \right]_{\mathrm{1}} ^{\mathrm{3}} −\frac{\mathrm{84}}{\mathrm{5}}\left[\left({u}+\mathrm{7}\right)^{\mathrm{5}/\mathrm{2}} \right]_{\mathrm{1}} ^{\mathrm{3}} +\mathrm{49}\left[\left({u}+\mathrm{7}\right)^{\mathrm{3}/\mathrm{2}} \right]_{\mathrm{1}} ^{\mathrm{3}} \\ $$$$=… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *