Menu Close

Question-91303

Tinku Tara 0 Comments
Pin




Question Number 91303 by 174 last updated on 29/Apr/20
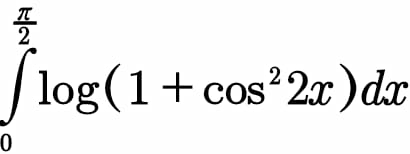
Commented by mathmax by abdo last updated on 29/Apr/20
A =∫_0 ^(π/2) ln(1+cos^2 (2x))dx ⇒A =∫_0 ^(π/2) ln(1+((1+cos(4x))/2))dx =∫_0 ^(π/2) ln(3+cos(4x))dx−(π/2)ln(2) we have ∫_0 ^(π/2) ln(3+cos(4x))dx =(π/2)ln(3)+∫_0 ^(π/2) ln(1+(1/3)cos(4x))dx (4x=t) =(π/2)ln(3) +(1/4)∫_0 ^π ln(1+(1/3)cost) ⇒ A =(π/2)ln(3)−(π/2)ln(2) +(1/4)∫_0 ^π ln(1+(1/3)cost)dt let f(a) =∫_0 ^π ln(1+acost)dt with 0<a<1 we have f^′ (a) =∫_0 ^π ((cost)/(1+acost))dt =(1/a)∫_0 ^π ((1+acost−1)/(1+acost))dt =(π/a)−(1/a) ∫_0 ^π (dt/(1+acost)) we have ∫_0 ^π (dt/(1+acost)) =_(tan((t/2))=u) ∫_0 ^∞ ((2du)/((1+u^2 )(1+a×((1−u^2 )/(1+u^2 ))))) =∫_0 ^∞ ((2du)/(1+u^2 +a−au^2 )) =∫_0 ^∞ ((2du)/((1−a)u^2 +1+a))=(2/(1−a))∫_0 ^∞ (du/(u^2 +((1+a)/(1−a)))) =_(u=(√((1+a)/(1−a)))z) (2/(1−a))∫_0 ^∞ (1/(((1+a)/(1−a))(1+z^2 )))×(√((1+a)/(1−a)))dz =(2/( (√(1−a^2 ))))∫_0 ^∞ (dz/(1+z^2 )) =(2/( (√(1−a^2 ))))×(π/2) =(π/( (√(1−a^2 )))) ⇒ f^′ (a) =(π/a)−(π/(a(√(1−a^2 )))) ⇒f(a) =πln(a)−π ∫ (da/(a(√(1−a^2 )))) +c ∫ (da/(a(√(1−a^2 )))) =_(a =sinx) ∫ ((cosxdx)/(sinx×cosx)) =∫(dx/(sinx)) =_(tan((x/2))=u) ∫ ((2du)/((1+u^2 )×((2u)/(1+u^2 )))) =∫(du/u) =ln∣u∣=ln∣tan((x/2))∣ =ln∣tan((1/2)arcsina)∣ ⇒ f(a) =πln(a)−πln∣tan((1/2)arcsina)∣ +c f(a) =πln((a/(∣tan((1/2)arcsina)∣))) +c (1/2)arcsina ∼(a/2) ⇒tan(((arcsina)/2))∼(a/2) ⇒f(a) ∼πln(2)+c (a∼0) ⇒lim_(a→0) f(a) =0 =πln(2)+c ⇒c =−πln(2) ⇒ f(a) =πln(a)−πln(2)−πln∣tan((1/2)arcsina)∣ so ∫_0 ^π ln(1+(1/3)cost)dt =f((1/3))=−πln(3)−πln(2) −πln∣tan((1/2)arcsin((1/3))∣ ⇒ A =(π/2)ln(3)−(π/2)ln(2)−(π/4)ln(3)−(π/4)ln(2)−(π/4)ln∣tan((1/2)arcsin((1/3))∣ A =(π/4)ln(3)−((3π)/4)ln(2)−(π/4)ln∣tan((1/2)arcsin((1/3))∣
$${A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+{cos}^{\mathrm{2}} \left(\mathrm{2}{x}\right)\right){dx}\:\Rightarrow{A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+\frac{\mathrm{1}+{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{3}+{cos}\left(\mathrm{4}{x}\right)\right){dx}−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:{we}\:{have} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{3}+{cos}\left(\mathrm{4}{x}\right)\right){dx}\:=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{3}\right)+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}{cos}\left(\mathrm{4}{x}\right)\right){dx}\:\:\left(\mathrm{4}{x}={t}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{3}\right)\:+\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\pi} {ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}{cost}\right)\:\Rightarrow \\ $$$${A}\:=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{3}\right)−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:+\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\pi} {ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}{cost}\right){dt}\:{let} \\ $$$${f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\pi} {ln}\left(\mathrm{1}+{acost}\right){dt}\:\:\:{with}\:\mathrm{0}<{a}<\mathrm{1} \\ $$$${we}\:{have}\:{f}^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\:\frac{{cost}}{\mathrm{1}+{acost}}{dt}\:=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{1}+{acost}−\mathrm{1}}{\mathrm{1}+{acost}}{dt} \\ $$$$=\frac{\pi}{{a}}−\frac{\mathrm{1}}{{a}}\:\int_{\mathrm{0}} ^{\pi} \:\frac{{dt}}{\mathrm{1}+{acost}}\:\:{we}\:{have}\: \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\frac{{dt}}{\mathrm{1}+{acost}}\:=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}×\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }\right)} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} +{a}−{au}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{du}}{\left(\mathrm{1}−{a}\right){u}^{\mathrm{2}} \:+\mathrm{1}+{a}}=\frac{\mathrm{2}}{\mathrm{1}−{a}}\int_{\mathrm{0}} ^{\infty} \frac{{du}}{{u}^{\mathrm{2}} \:+\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}} \\ $$$$=_{{u}=\sqrt{\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}}{z}} \:\:\:\:\frac{\mathrm{2}}{\mathrm{1}−{a}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}\left(\mathrm{1}+{z}^{\mathrm{2}} \right)}×\sqrt{\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}}{dz} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\int_{\mathrm{0}} ^{\infty} \frac{{dz}}{\mathrm{1}+{z}^{\mathrm{2}} }\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}×\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\:\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\:\Rightarrow \\ $$$${f}^{'} \left({a}\right)\:=\frac{\pi}{{a}}−\frac{\pi}{{a}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\:\Rightarrow{f}\left({a}\right)\:=\pi{ln}\left({a}\right)−\pi\:\int\:\:\:\frac{{da}}{{a}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\:+{c} \\ $$$$\int\:\:\frac{{da}}{{a}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\:=_{{a}\:={sinx}} \:\:\:\int\:\:\frac{{cosxdx}}{{sinx}×{cosx}}\:=\int\frac{{dx}}{{sinx}} \\ $$$$=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={u}} \:\:\:\:\int\:\frac{\mathrm{2}{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)×\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}\:=\int\frac{{du}}{{u}}\:={ln}\mid{u}\mid={ln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)\mid \\ $$$$={ln}\mid{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arcsina}\right)\mid\:\Rightarrow \\ $$$${f}\left({a}\right)\:=\pi{ln}\left({a}\right)−\pi{ln}\mid{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arcsina}\right)\mid\:+{c} \\ $$$${f}\left({a}\right)\:=\pi{ln}\left(\frac{{a}}{\mid{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arcsina}\right)\mid}\right)\:+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{arcsina}\:\sim\frac{{a}}{\mathrm{2}}\:\Rightarrow{tan}\left(\frac{{arcsina}}{\mathrm{2}}\right)\sim\frac{{a}}{\mathrm{2}}\:\Rightarrow{f}\left({a}\right)\:\sim\pi{ln}\left(\mathrm{2}\right)+{c}\:\left({a}\sim\mathrm{0}\right) \\ $$$$\Rightarrow{lim}_{{a}\rightarrow\mathrm{0}} {f}\left({a}\right)\:=\mathrm{0}\:=\pi{ln}\left(\mathrm{2}\right)+{c}\:\Rightarrow{c}\:=−\pi{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$${f}\left({a}\right)\:=\pi{ln}\left({a}\right)−\pi{ln}\left(\mathrm{2}\right)−\pi{ln}\mid{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arcsina}\right)\mid\:{so} \\ $$$$\int_{\mathrm{0}} ^{\pi} {ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}{cost}\right){dt}\:={f}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=−\pi{ln}\left(\mathrm{3}\right)−\pi{ln}\left(\mathrm{2}\right) \\ $$$$−\pi{ln}\mid{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arcsin}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\mid\:\Rightarrow\right. \\ $$$${A}\:=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{3}\right)−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)−\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{3}\right)−\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)−\frac{\pi}{\mathrm{4}}{ln}\mid{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arcsin}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\mid\right. \\ $$$${A}\:=\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{3}\right)−\frac{\mathrm{3}\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)−\frac{\pi}{\mathrm{4}}{ln}\mid{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arcsin}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\mid\right. \\ $$
Commented by 174 last updated on 30/Apr/20
thanks alot
Commented by mathmax by abdo last updated on 30/Apr/20
you are welcome
$${you}\:{are}\:{welcome} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *